B. The Corridor or There and Back Again
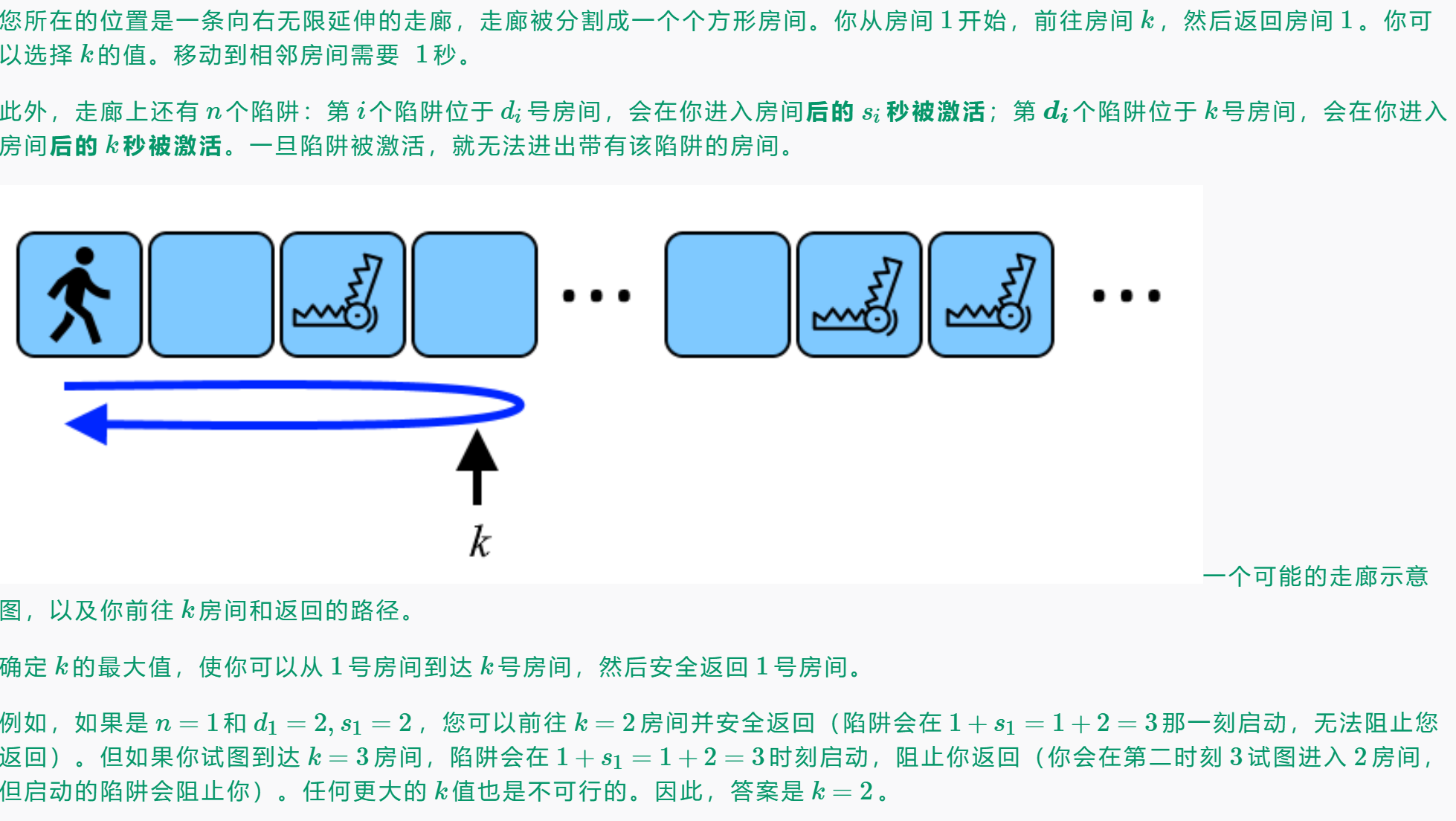
题解
- 考虑二分答案
- \(check\)时判断是否\(s_i \leq 2*(k - d_i),k\geq d_i\)
const int N = 2e5 + 10, M = 4e5 + 10;
int n, d[N], s[N];
bool check(int mid)
{
for (int i = 1; i <= n; ++i)
{
if (d[i] <= mid)
{
if (s[i] <= 2 * (mid - d[i]))
return false;
}
}
return true;
}
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> d[i] >> s[i];
int l = 1, r = 1e15;
while (l <= r)
{
int mid = l + r >> 1;
if (check(mid))
l = mid + 1;
else
r = mid - 1;
}
cout << r << endl;
}
C. Non-coprime Split

题解
- 容易发现一个大于1的非质数\(x\)一定可以由其约数\(y\)和\(x - y\)相加得到,且\(gcd(x-y,y)\neq1\)
- 直接暴力找大于1的非质数即可
const int N = 2e5 + 10, M = 4e5 + 10;
bool is_prime(int x, int &b)
{
if (x < 2)
return false;
for (int i = 2; i <= x / i; ++i)
{
if (x % i == 0)
{
b = i;
return false;
}
}
return true;
}
void solve()
{
int l, r;
cin >> l >> r;
int res = INF;
int b = -1;
for (int i = l; i <= r; ++i)
{
if (!is_prime(i, b) && i > 2)
{
res = i;
break;
}
}
if (res == INF)
cout << -1 << endl;
else
{
cout << b << " " << res - b << endl;
}
}
D. Plus Minus Permutation

题解
- 贪心考虑,对于整除\(x\)的位置一定从\(n\)开始放,对于整除\(y\)的位置一定从\(1\)开始放
- 但是存在同时整除\(x\)和\(y\)的情况
- 求出\(lcm(x,y)\),即可得到重合的位置数量\(n/lcm(x,y)\)
- 减去重合的位置数量后等差数列求和即可
const int N = 2e5 + 10, M = 4e5 + 10;
int n, x, y;
void solve()
{
cin >> n >> x >> y;
int t1 = n / x, t2 = n / y;
int lc = lcm(x, y);
int t3 = n / lc;
t1 -= t3, t2 -= t3;
cout << (n - t1 + 1 + n) * t1 / 2 - (1 + t2) * t2 / 2 << endl;
}
E. Data Structures Fan

题解
- 不会思维,赛时直接上线段树了
- 线段树维护区间二进制为\(0\)的位置上的异或和\(ans0\),区间二进制为\(0\)的位置上的异或和\(ans1\)
- 考虑区间反转操作:直接交换\(ans0\)和\(ans1\)即可,并打上懒惰标记
const int N = 1e5 + 10, M = 4e5 + 10;
int n, q, a[N];
string s;
struct info
{
int ans0, ans1;
friend info operator+(const info &a, const info &b)
{
info c;
c.ans0 = a.ans0 ^ b.ans0;
c.ans1 = a.ans1 ^ b.ans1;
return c;
}
};
struct SEG
{
int lazy;
info val;
} seg[N << 2];
void up(int id)
{
seg[id].val = seg[lson].val + seg[rson].val;
}
void settag(int id, int tag)
{
swap(seg[id].val.ans0, seg[id].val.ans1);
seg[id].lazy ^= tag;
}
void down(int id)
{
if (seg[id].lazy == 0)
return;
settag(lson, seg[id].lazy);
settag(rson, seg[id].lazy);
seg[id].lazy = 0;
}
void build(int id, int l, int r)
{
seg[id].lazy = 0;
if (l == r)
{
if (s[l] == '1')
{
seg[id].val.ans0 = 0;
seg[id].val.ans1 = a[l];
}
else
{
seg[id].val.ans0 = a[l];
seg[id].val.ans1 = 0;
}
return;
}
int mid = l + r >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
up(id);
}
void modify(int id, int l, int r, int ql, int qr, int tag)
{
if (ql <= l && r <= qr)
{
settag(id, tag);
return;
}
down(id);
int mid = l + r >> 1;
if (qr <= mid)
modify(lson, l, mid, ql, qr, tag);
else if (ql > mid)
modify(rson, mid + 1, r, ql, qr, tag);
else
{
modify(lson, l, mid, ql, qr, tag);
modify(rson, mid + 1, r, ql, qr, tag);
}
up(id);
}
info query(int id, int l, int r, int ql, int qr)
{
if (ql <= l && r <= qr)
return seg[id].val;
down(id);
int mid = l + r >> 1;
if (qr <= mid)
return query(lson, l, mid, ql, qr);
else if (ql > mid)
return query(rson, mid + 1, r, ql, qr);
else
return query(lson, l, mid, ql, qr) + query(rson, mid + 1, r, ql, qr);
}
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
cin >> s;
s = " " + s;
build(1, 1, n);
cin >> q;
while (q--)
{
int op, l, r, g;
cin >> op;
if (op == 1)
{
cin >> l >> r;
modify(1, 1, n, l, r, 1);
}
else
{
cin >> g;
if (g == 0)
cout << query(1, 1, n, 1, n).ans0 << " ";
else
cout << query(1, 1, n, 1, n).ans1 << " ";
}
}
cout << endl;
}
F. Selling a Menagerie

题解
- 跑个拓扑排序,不在环上的随便放,然后对每个环上的从每个起点都跑一次找到贡献最大的起点
- 枚举起点的过程类似滑动窗口更新即可
- 可以断环成链方便一点
const int N = 1e5 + 10, M = 4e5 + 10;
int n, a[N], c[N], deg[N], vis[N], b[N];
vector<int> g[N];
void dfs(int u, vector<int> &vec)
{
vis[u] = true;
vec.push_back(u);
for (auto v : g[u])
{
if (!vis[v])
dfs(v, vec);
}
}
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
g[i].clear(), deg[i] = vis[i] = 0;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
g[i].push_back(a[i]);
deg[a[i]]++;
}
for (int i = 1; i <= n; ++i)
cin >> c[i];
queue<int> q;
for (int i = 1; i <= n; ++i)
{
if (deg[i] == 0)
q.push(i);
}
vector<int> ans;
while (q.size())
{
int u = q.front();
vis[u] = true;
q.pop();
ans.push_back(u);
for (auto v : g[u])
{
if (--deg[v] == 0)
q.push(v);
}
}
for (int i = 1; i <= n; ++i)
{
vector<int> vec;
if (vis[i])
continue;
if (!vis[i])
dfs(i, vec);
int mx = 0, pos = 1, idx = 0;
for (auto x : vec)
b[++idx] = x;
for (int i = 1; i <= idx; ++i)
b[i + idx] = b[i];
int sum = 0;
for (int i = 1; i <= idx - 1; ++i)
sum += 2 * c[b[i]];
sum += c[b[idx]];
mx = sum;
for (int i = 2; i <= idx; ++i)
{
sum -= c[b[i - 1]];
sum += c[b[i + idx - 1 - 1]];
if (mx < sum)
{
sum = mx;
pos = i;
}
}
for (int i = pos; i <= pos + idx - 1; ++i)
ans.push_back(b[i]);
}
for (auto u : ans)
cout << u << " ";
cout << endl;
}
G. Replace With Product

题解
- 首先序列两边的\(1\)完全可以用来加,所以我们处理出左边第一个不是\(1\)的位置\(l\),同理处理出\(r\)
- 从位置\(l\)开始乘,设\(res\)为乘积
- 如果乘到某个位置\(x\)时\(res\geq 1e9\),容易证明:对于区间\([x + 1, r]\)里面的数字,乘起来的和一定由于加起来的和
- 所以\([l,r]\)这段区间我们可以全选
- 如果最终\(res < 1e9\),说明\(\geq 2\)的数的个数小于\(m = log(1e9)\)个,直接\(O(m^2)\)暴力枚举选择哪段区间为乘积即可
- 后面的过程模拟即可,注意区间中存在\(1\),模拟时注意细节即可
const int N = 2e5 + 10, M = 4e5 + 10;
int n, a[N], b[N], idx;
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
int l = 1, r = n;
while (a[l] == 1 && l < r)
l++;
while (a[r] == 1 && l < r)
r--;
int res = 1;
for (int i = l; i <= r; ++i)
{
res *= a[i];
if (res > 1e9)
{
cout << l << " " << r << endl;
return;
}
}
idx = 0;
int sum = 0;
for (int i = 1; i <= n; ++i)
{
if (a[i] > 1)
b[++idx] = i;
sum += a[i];
}
int ans = sum, ansl = 1, ansr = 1;
for (int i = 1; i <= idx; ++i)
{
res = 1;
l = b[i];
int s = 0;
for (int j = i; j <= idx; ++j)
{
res *= a[b[j]];
r = b[j];
s += a[b[j]];
int val = sum - s - (r - l + 1 - (j - i + 1)) + res;
if (val > ans)
{
ans = val;
ansl = l, ansr = r;
}
}
}
cout << ansl << " " << ansr << endl;
}







