二维基础

前置知识

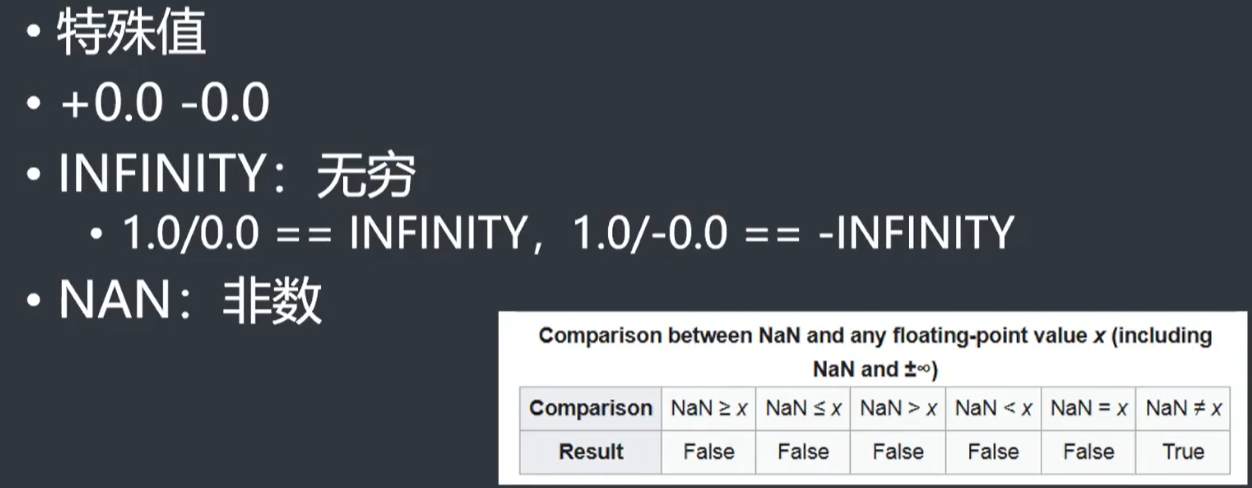
浮点数与精度问题

若问题能用整数解决则不用浮点数

别用\(float\)，视情况用\(long\ double\)

减少数学函数的使用(开方、三角函数)

比较时加入容限，即\(eps\)

点

const double PI = acos(-1.0);
const double eps = 1e-9;

struct Point
{
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y){};
    Point operator+(Point t)
    {
        return Point(x + t.x, y + t.y);
    }
    Point operator-(Point t)
    {
        return Point(x - t.x, y - t.y);
    }
    Point operator*(double k)
    {
        return Point(x * k, y * k);
    }
    Point operator/(double k)
    {
        return Point(x / k, y / k);
    }
    bool operator==(Point t)
    {
        return sgn(x - t.x) == 0 && sgn(y - t.y) == 0;
    }
};
typedef Point Vector;

int sgn(double x)
{
    if (fabs(x) < eps)
        return 0; 
    else
        return x < 0 ? -1 : 1;
}

int dcmp(double x, double y)
{
    if (fabs(x - y) < eps)
        return 0;
    else
        return x < y ? -1 : 1;
}

向量

直接用\(Point\)表示即可
typedef Point Vector;

点积

double dot(Vector &a, Vector &b)
{
    return a.x * b.x + a.y * b.y;
}

叉积

\(to\_left\)测试

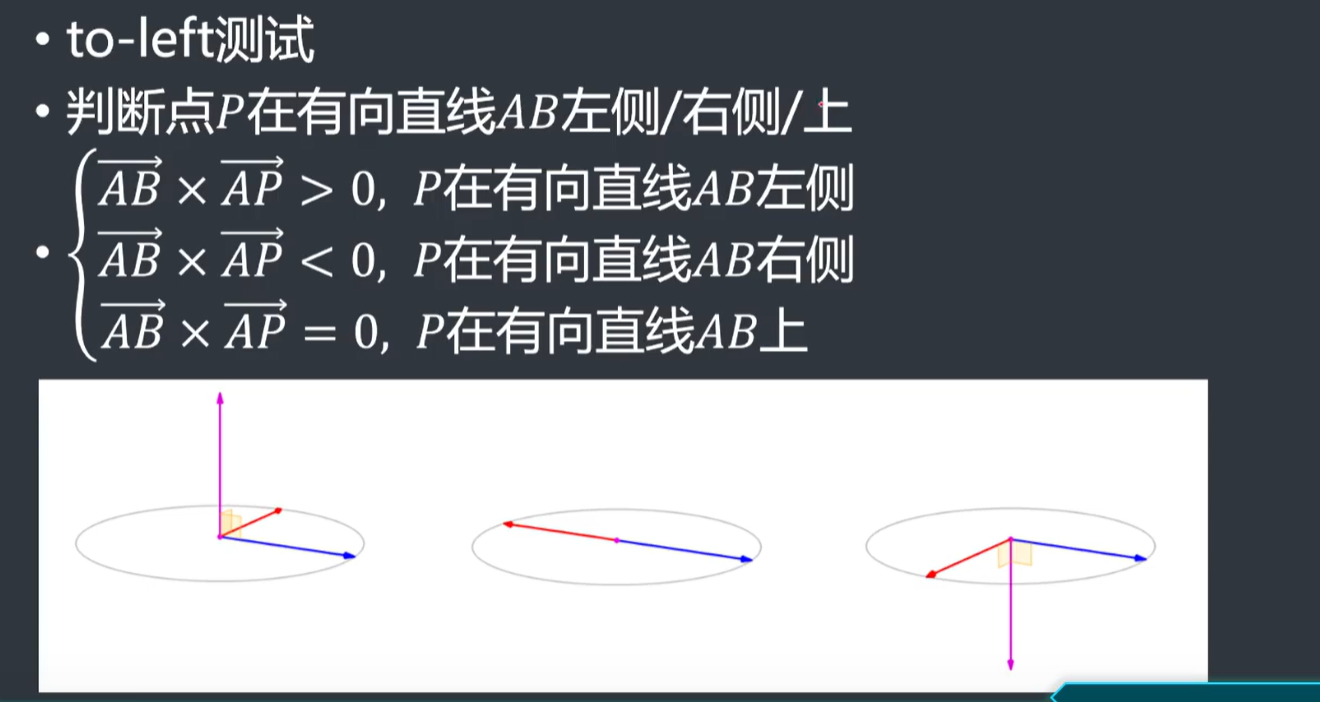
向量旋转

线段

判断点是否在线段上

判断两个线段是否相交

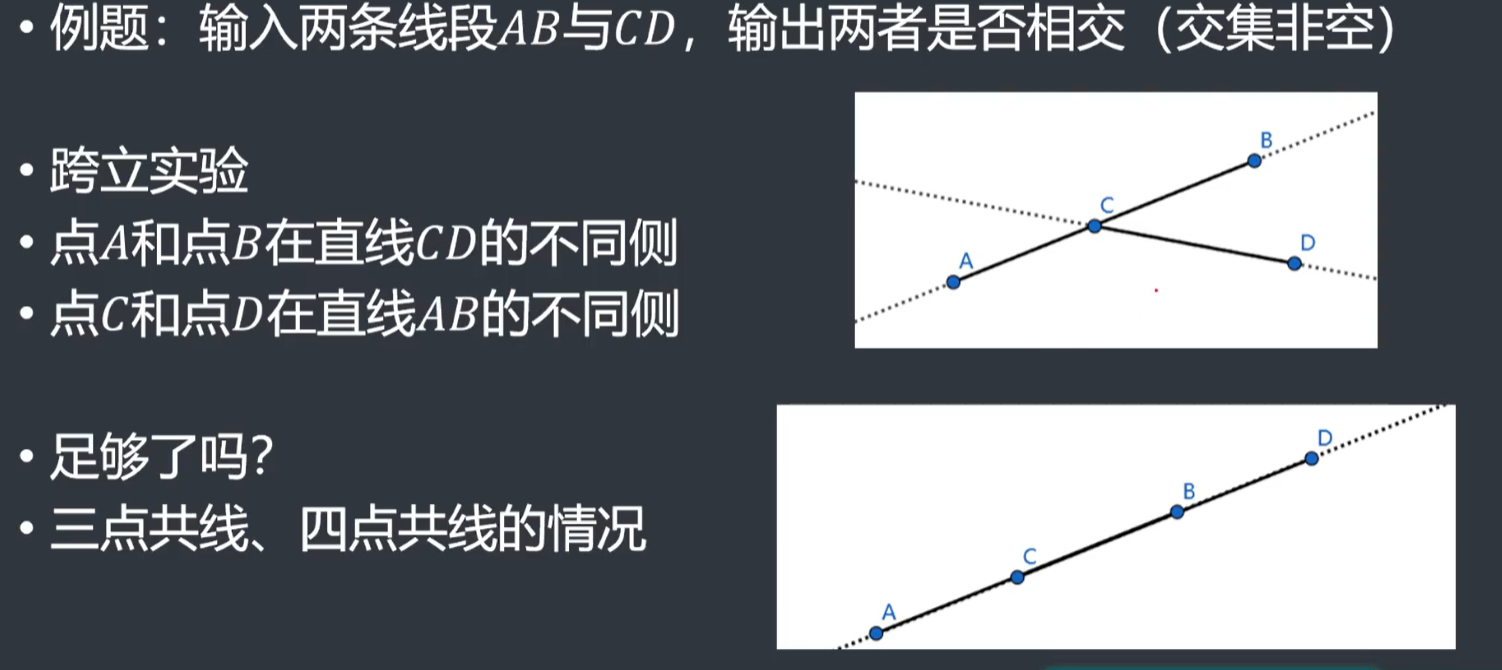
直线

斜截式：\(y = kx + b\)

截距式：\(\frac{x}{a} + \frac{x}{b} = 1\)

一般式：\(Ax + By + C = 0\)

点斜式：\(y - y_1 = k(x - x_1)\)

但是上面的我们不推荐使用，我们考虑使用点向式

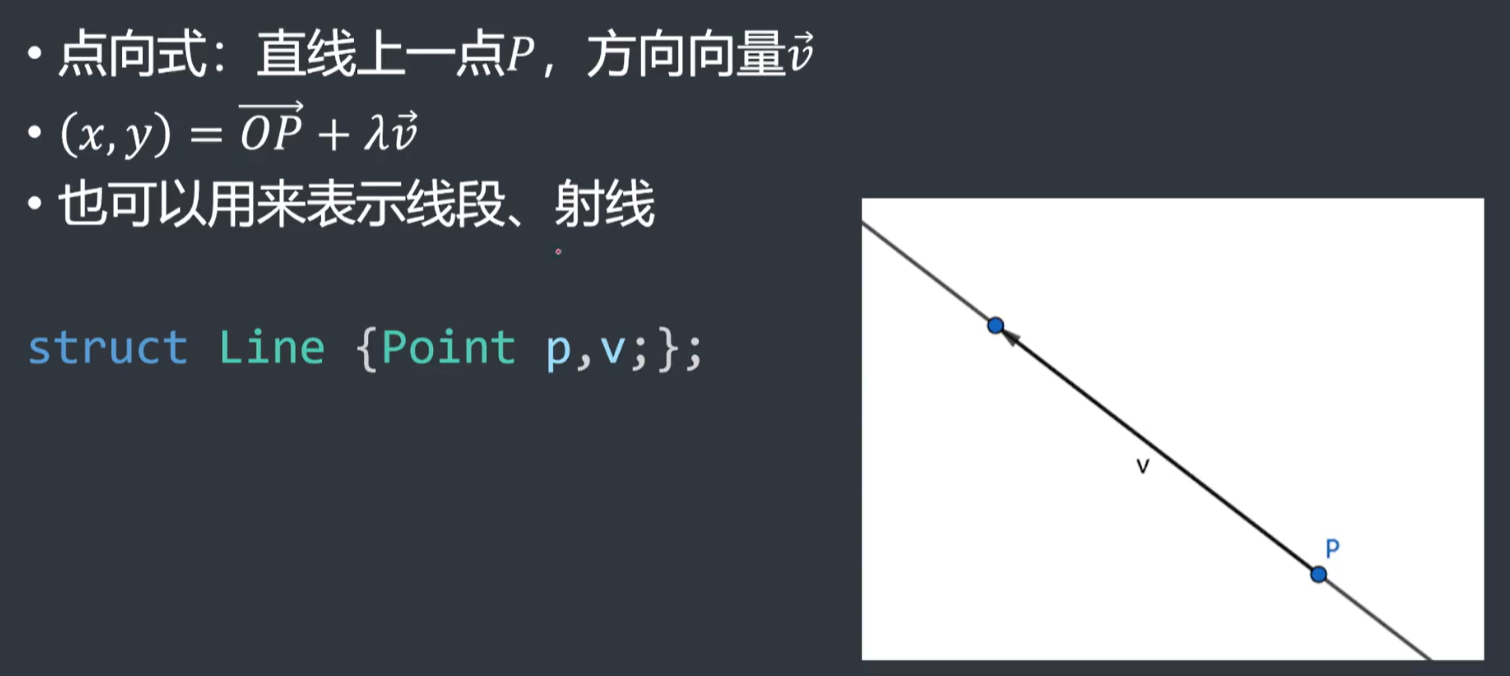
点向式：直线上一点\(P\)，以及方向向量\(\vec{v}\)

点到直线的距离

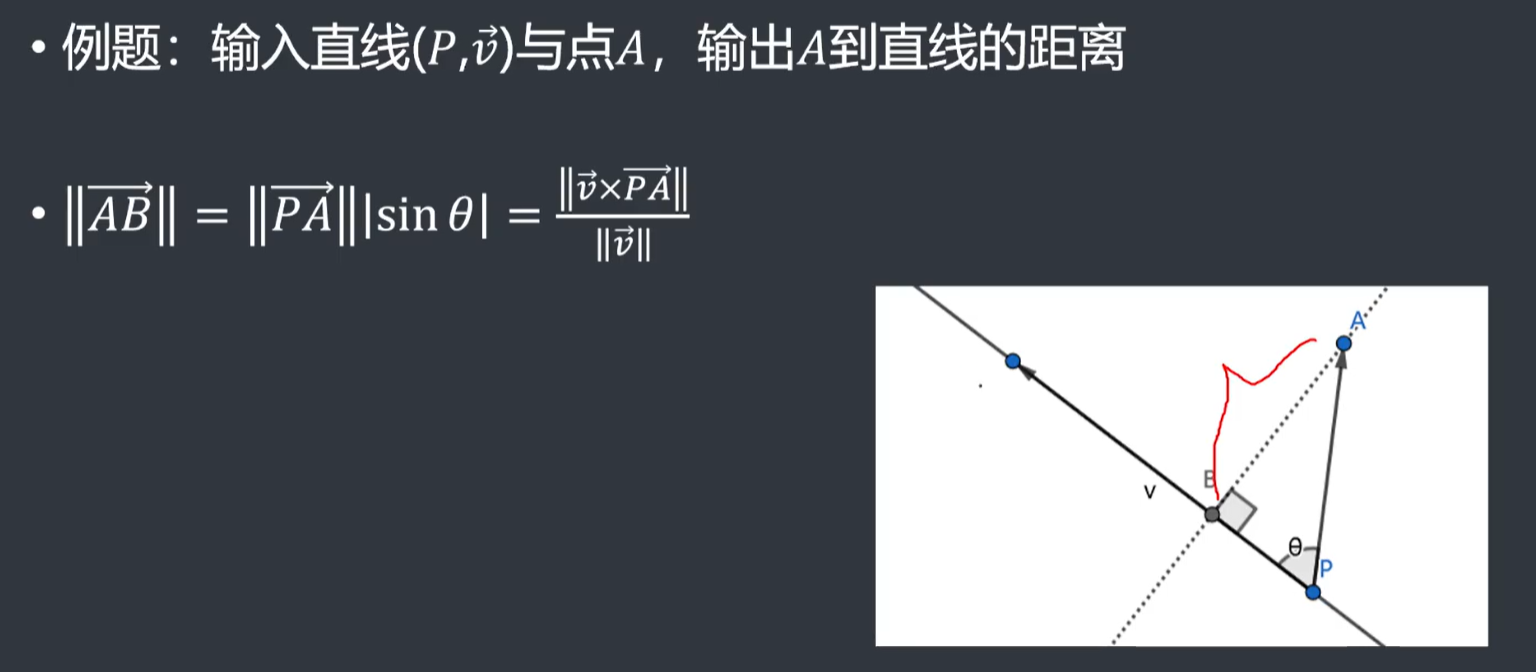
点在直线上的投影

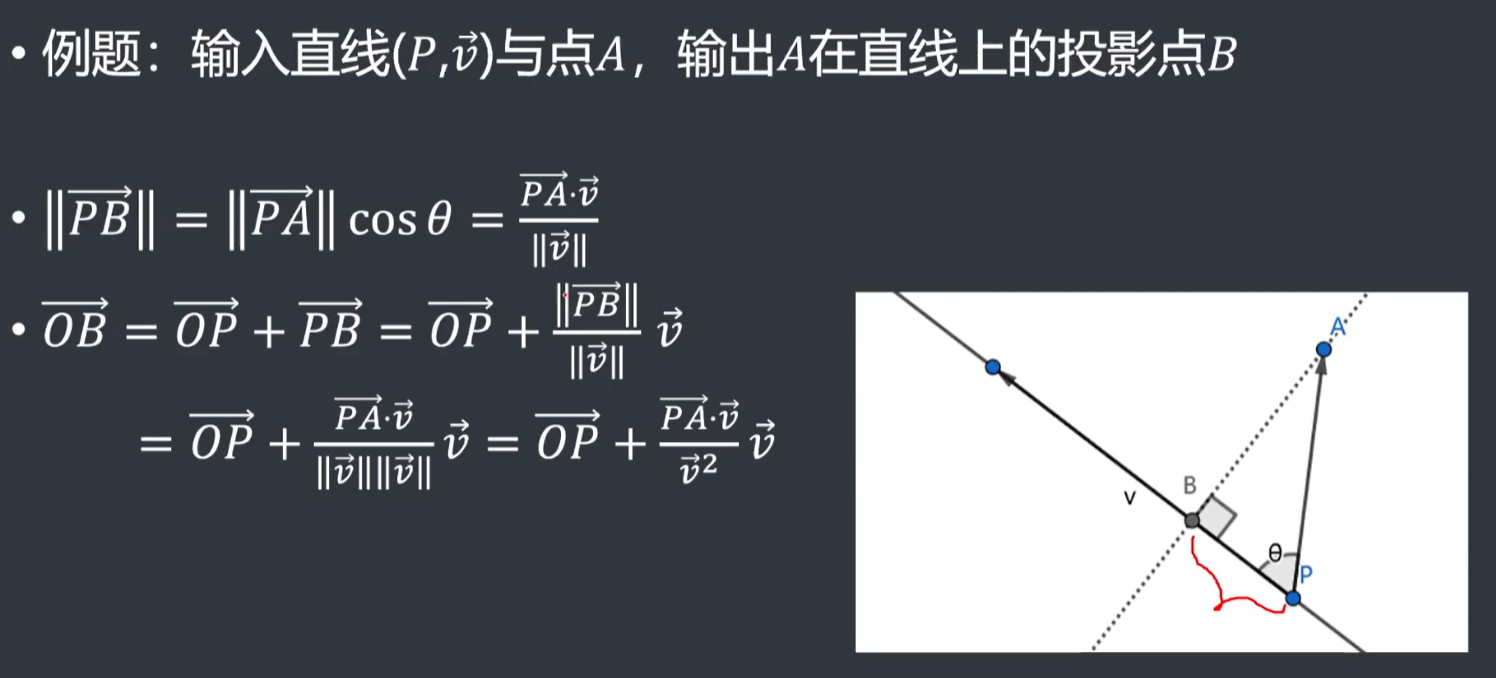
两直线的交点

运用了正弦定理和叉积来求交点

然后我们可以通过点向式求出交点的坐标

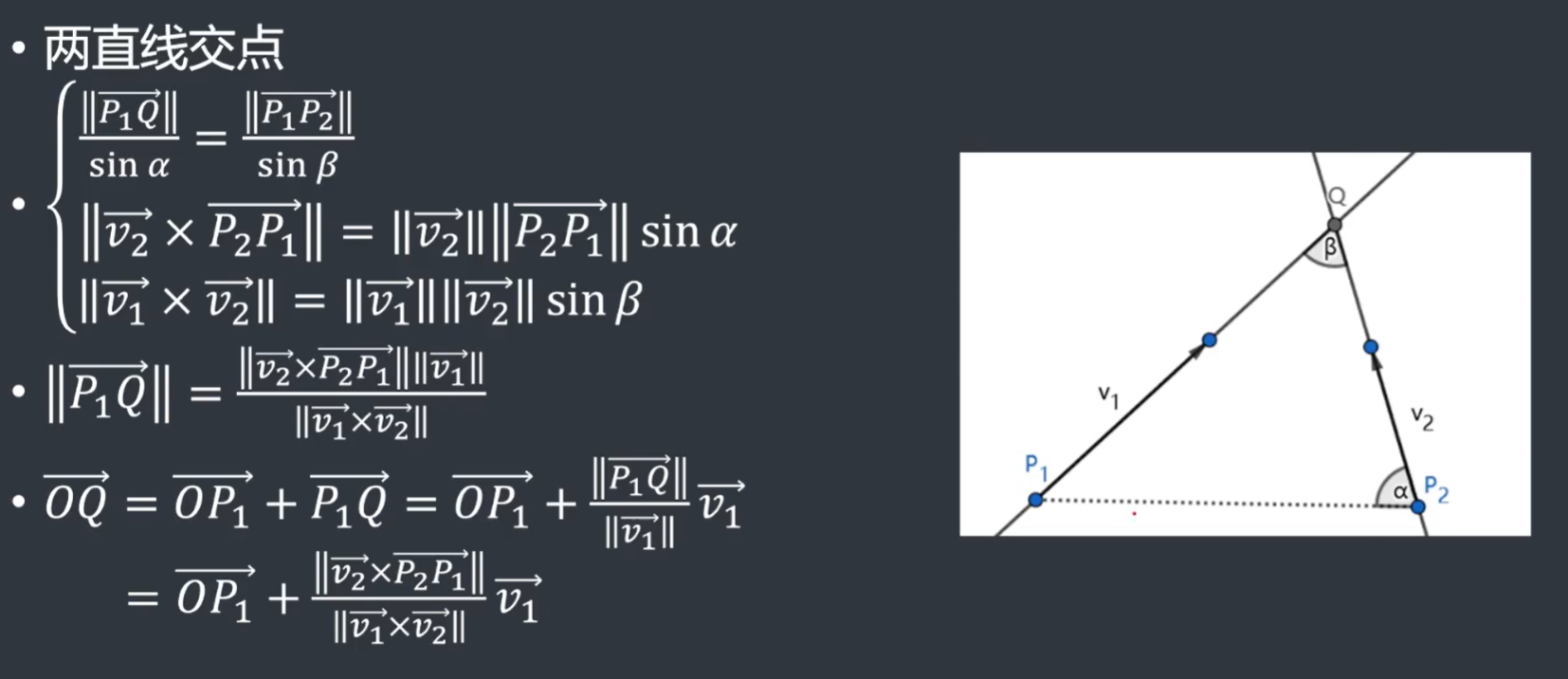
多边形

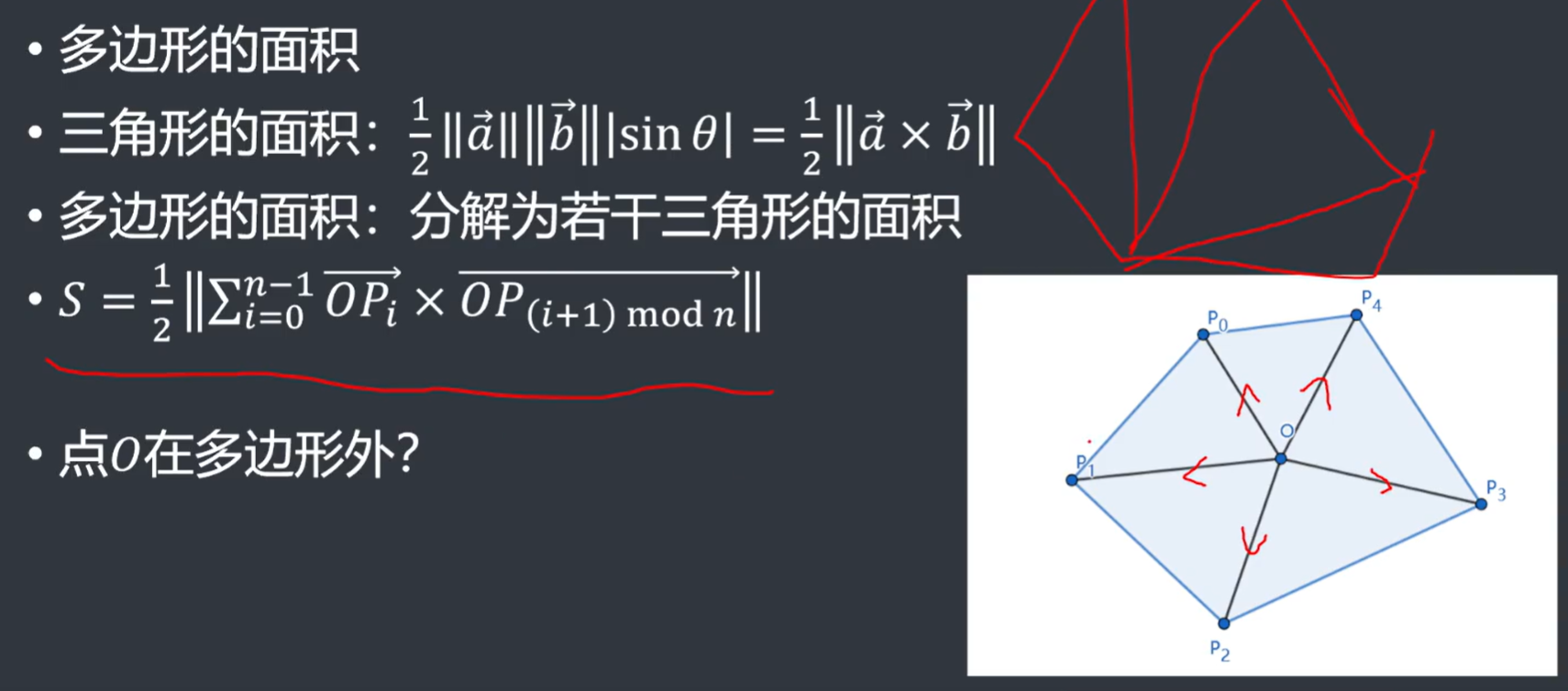
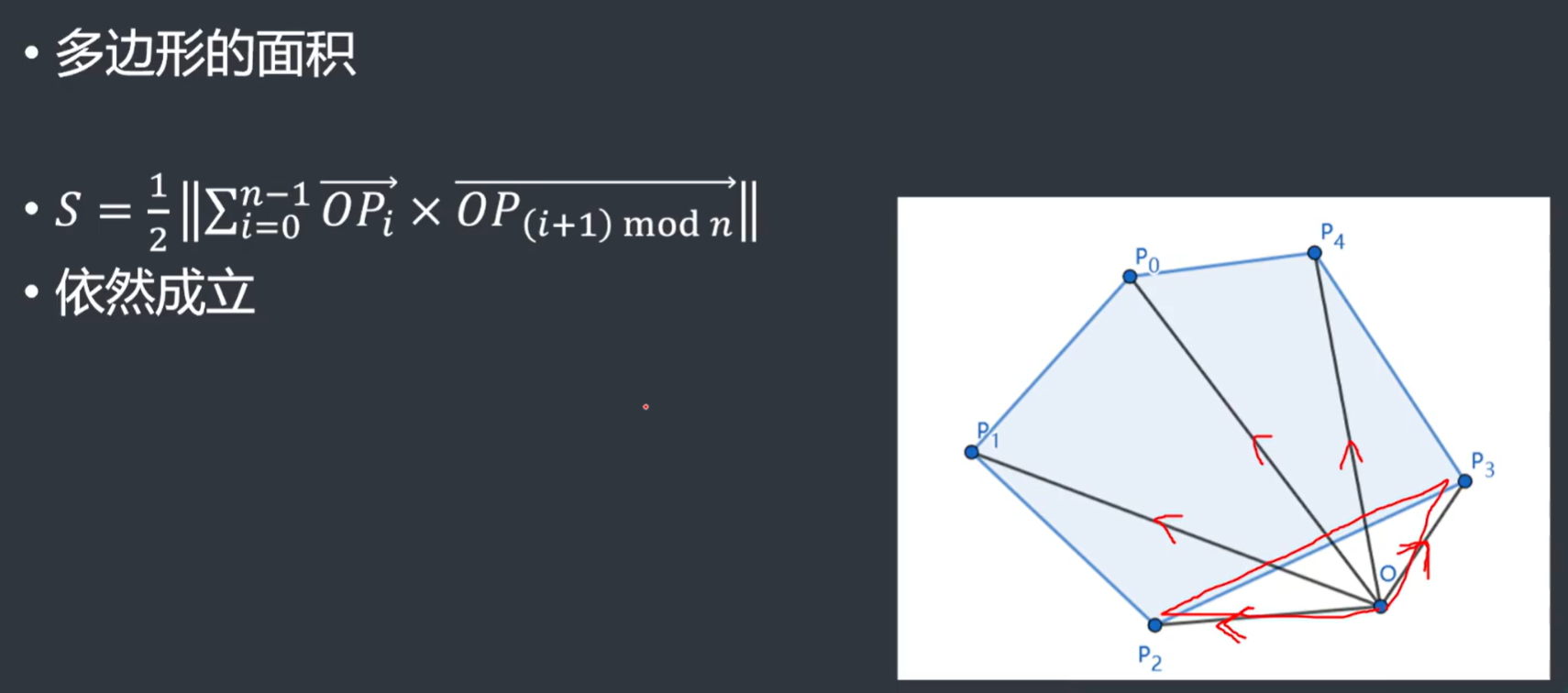
多边形的面积

原点\(O\)在多边形外结论同样成立的原因在于：

我们发现我们需要容斥删掉一个三角形的面积

但是叉积是有正负的

我们惊喜的发现需要删掉的三角形的叉积恰好是负数，而其余三角形都为正数

注意：计算面积时应该所有叉积累加之后再取模

对于非凸多边形来说结论也同样成立

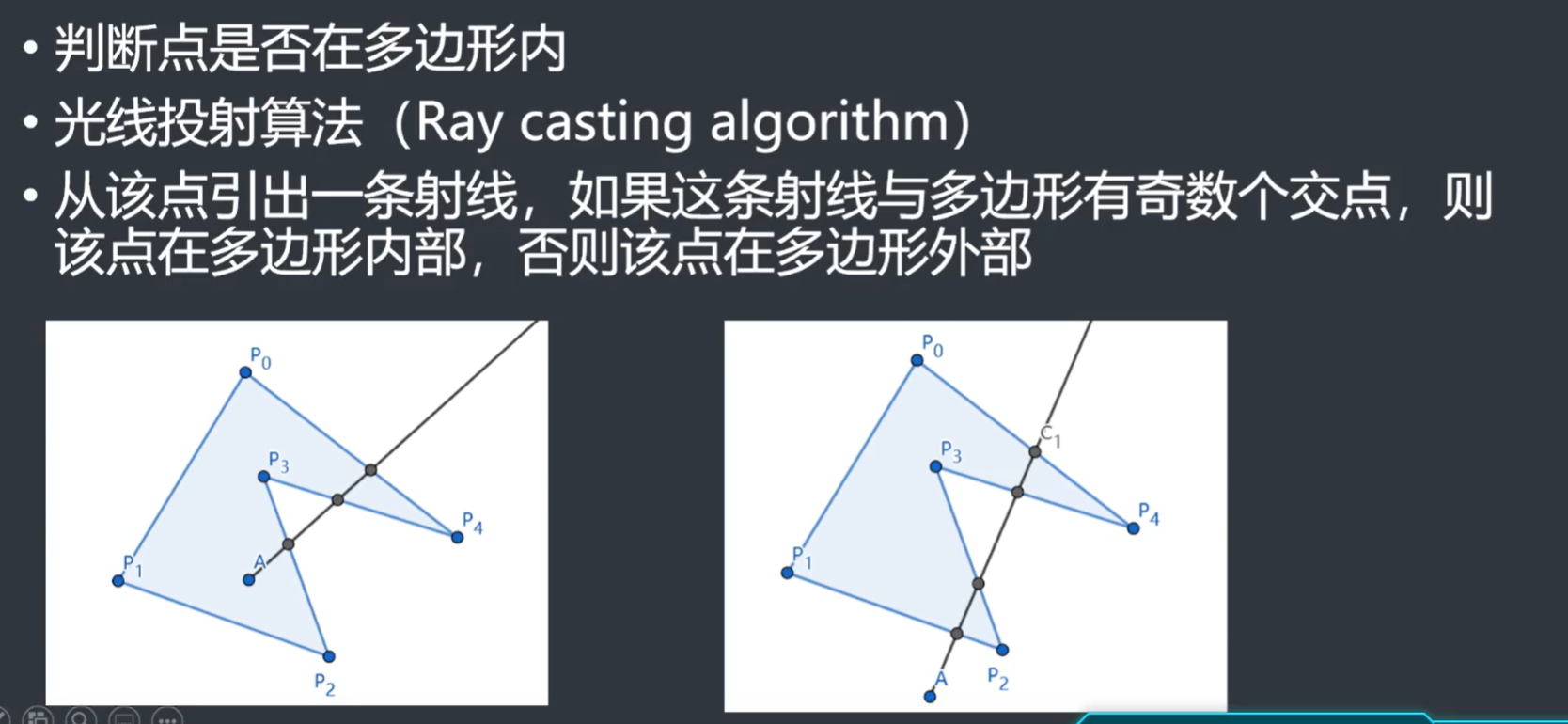
判断点是否在多边形内部

光线投射法

但是存在退化现象，即存在很多边界条件，需要特判

并且射线的方向是自己定的，并不方便

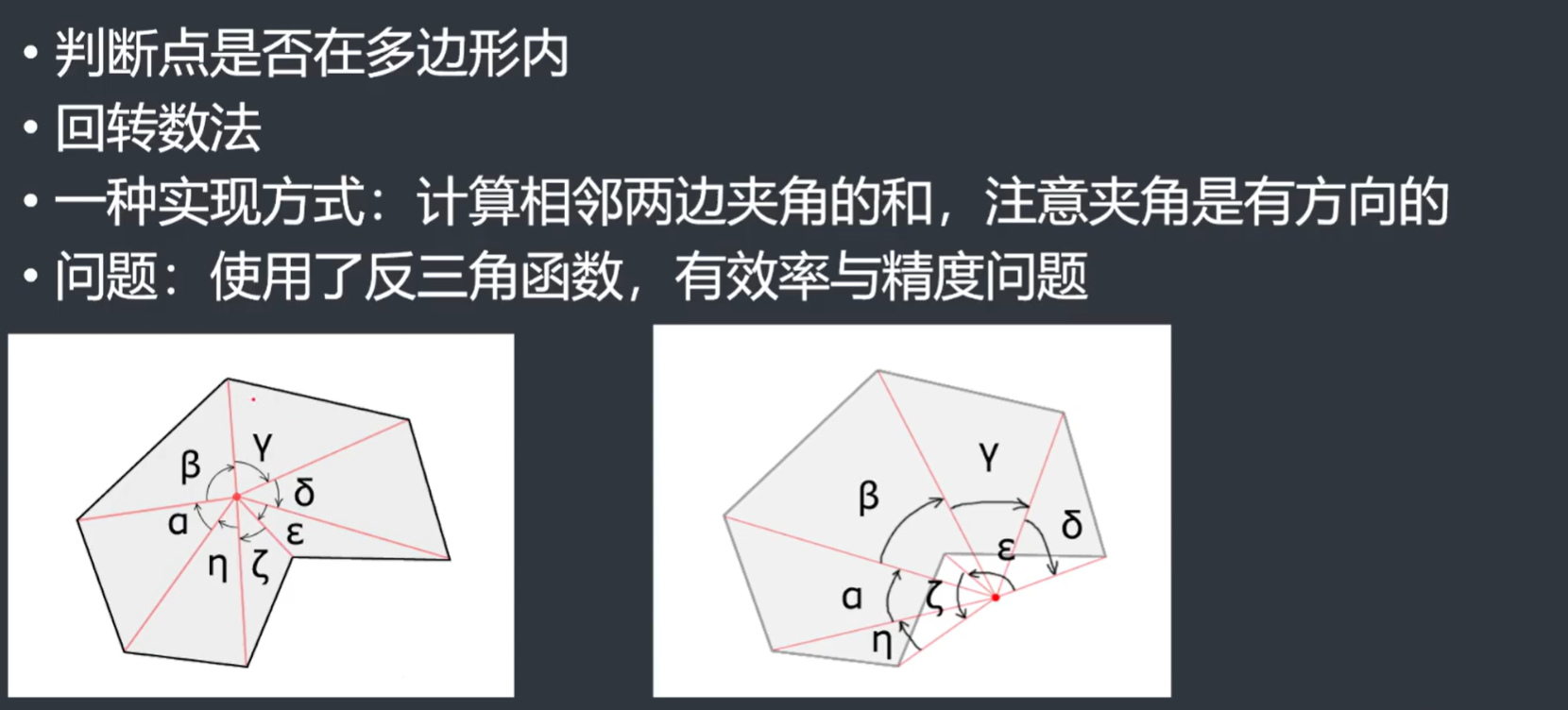
回转数法

我们算出所有角度之和，如果顺时针就加上该角度，如果逆时针就减去该角度

如果最后角度之和为\(0\)，代表点在多边形外，否则在多边形内

但是该方法需要用到反三角函数求角度，存在效率和精度的问题

那有没有更加精确且快速的方法呢？

我们可以将光线投射法推广到回转数法中

光线投射法在回转数法上的推广

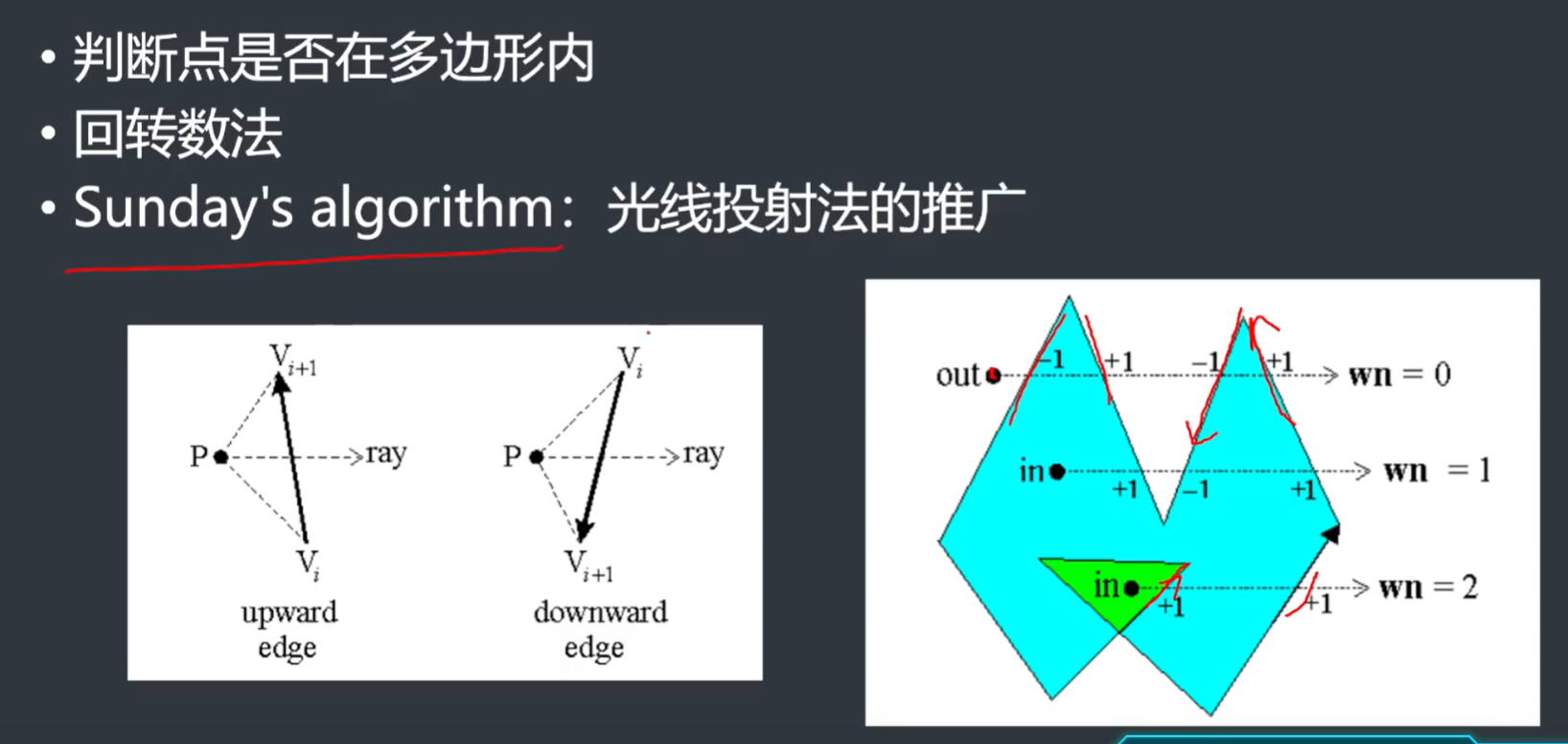
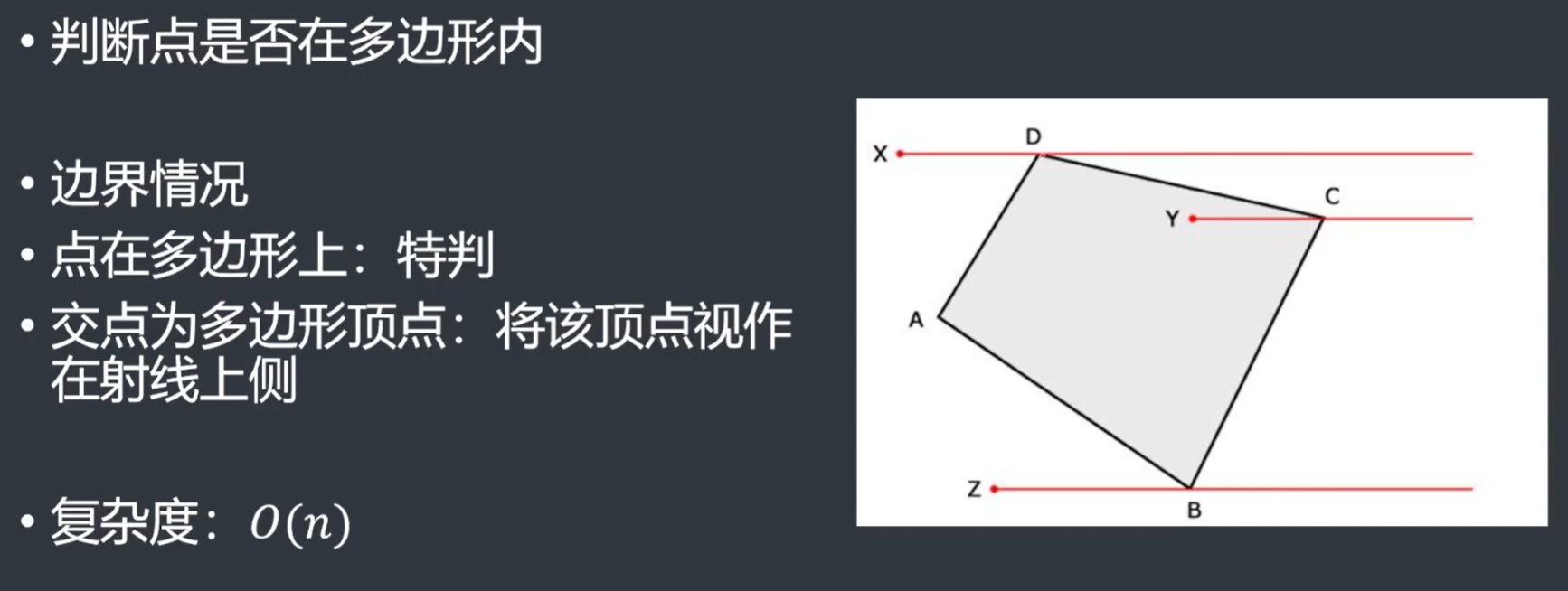
但是还存在一些边界情况我们需要特判，或者说需要特殊处理

重点是如果交点为多边形顶点，我们需要将该顶点视作在射线上侧

我们分析复杂度：

因为要遍历每一条边

所以复杂度为\(O(n)\)

对于一个凸多边形来说，我们存在其他的方法来判断一个点是否在凸多边形内部

我们可以考虑\(n\)次\(to\_left\)测试

模板

const double eps = 1e-9;

using point_type = long double;

// 点与向量
template <typename T>
struct point
{
    T x, y;
    bool operator==(const point &a) const
    {
        return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
    }
    bool operator<(const point &a) const
    {
        if (fabs(x - a.x) <= eps)
            return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const point &a) const
    {
        return !(*this < a || *this == a);
    }
    point operator+(const point &a) const
    {
        return {x + a.x, y + a.y};
    }
    point operator-(const point &a) const
    {
        return {x - a.x, y - a.y};
    }
    point operator-() const
    {
        return {-x, -y};
    }
    point operator*(const T k) const
    {
        return {k * x, k * y};
    }
    point operator/(const T k) const
    {
        return {x / k, y / k};
    }
    // 点积
    T operator*(const point &a) const
    {
        return x * a.x + y * a.y;
    }
    // 叉积
    T operator^(const point &a) const
    {
        return x * a.y - y * a.x;
    }
    // to_left 测试
    int to_left(const point &a) const
    {
        auto t = (*this) ^ a;
        return (t > eps) - (t < -eps);
    }
    // 模长的平方
    T quad_len() const
    {
        return (*this) * (*this);
    }
    // 两点距离的平方
    T quad_dis(const point &a) const
    {
        return (a - (*this)).quad_len();
    }
    // 向量模长
    long double len() const
    {
        return sqrtl(quad_len());
    }
    // 两点距离
    long double dis(const point &a) const
    {
        return sqrtl(quad_dis(a));
    }
    // 向量旋转
    point rotate(const long double rad) const
    {
        return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
    }
};
using Point = point<point_type>;

// 直线
template <typename T>
struct line
{
    // p 为直线上的一点， v 是方向向量
    point<T> p, v;
    bool operator==(const line &a) const
    {
        return v.to_left(a.v) == 0 && v.to_left(a.p) == 0;
    }
    int to_left(const point<T> &a) const
    {
        return v.to_left(a - p);
    }
    // 直线交点
    point<T> inter(const line &a) const
    {
        return p + v * ((a.v ^ (p - a.p)) / (v ^ a.v));
    }
    // 点到直线的距离
    long double dis(const point<T> &a) const
    {
        return abs(v ^ (a - p)) / v.len();
    }
    // 点在直线上的投影
    point<T> project(const point<T> &a) const
    {
        return p + v * ((a - p) * v / (v * v));
    }
};
using Line = line<point_type>;

// 线段
template <typename T>
struct segment
{
    point<T> a, b;

    // 判断点是否在线段上
    // -1 代表点在线段端点处， 0 代表点不在线段上， 1 代表点严格在线段上
    int is_on(const point<T> &p) const
    {
        // 点在端点处
        if (p == a || p == b)
            return -1;
        return (p - a).to_left(p - b) == 0 && (p - a) * (p - b) < -eps;
    }

    // 判断线段和直线是否相交
    // -1 直线经过线段端点, 0 线段和直线不相交, 1 线段和直线严格相交
    int is_inter(const line<T> &l) const
    {
        if (l.toleft(a) == 0 || l.toleft(b) == 0)
            return -1;
        return l.toleft(a) != l.toleft(b);
    }

    // 判断两线段是否相交
    // -1 在某一线段端点处相交, 0 两线段不相交, 1 两线段严格相交
    int is_inter(const segment<T> &s) const
    {
        if (is_on(s.a) || is_on(s.b) || s.is_on(a) || s.is_on(b))
            return -1;
        // 跨立实验
        const line<T> l{a, b - a}, ls{s.a, s.b - s.a};
        return l.toleft(s.a) * l.toleft(s.b) == -1 && ls.toleft(a) * ls.toleft(b) == -1;
    }
};
using Segment = segment<point_type>;

// 多边形
template <typename T>
struct polygon
{
    vector<point<T>> p; // 以逆时针顺序存储

    size_t nxt(const size_t i) const { return i == p.size() - 1 ? 0 : i + 1; }
    size_t pre(const size_t i) const { return i == 0 ? p.size() - 1 : i - 1; }

    // 回转数
    // 返回值第一项表示点是否在多边形边上
    // 对于狭义多边形，回转数为 0 表示点在多边形外，否则点在多边形内
    pair<bool, int> winding(const point<T> &a) const
    {
        int cnt = 0;
        for (size_t i = 0; i < p.size(); i++)
        {
            const point<T> u = p[i], v = p[nxt(i)];
            // 点在多边形上
            if (abs((a - u) ^ (a - v)) <= eps && (a - u) * (a - v) <= eps)
                return {true, 0};
            if (abs(u.y - v.y) <= eps)
                continue;
            const line<T> uv = {u, v - u};
            // 保证 u 和 v 所连成的线段能被从点a 射出的射线击中
            if (u.y < v.y - eps && uv.to_left(a) <= 0)
                continue;
            if (u.y > v.y + eps && uv.to_left(a) >= 0)
                continue;
            if (u.y < a.y - eps && v.y >= a.y - eps)
                cnt++;
            if (u.y >= a.y - eps && v.y < a.y - eps)
                cnt--;
        }
        return {false, cnt};
    }

    // 多边形面积的两倍
    // 可用于判断点的存储顺序是顺时针或逆时针
    T area() const
    {
        T sum = 0;
        for (size_t i = 0; i < p.size(); i++)
            sum += p[i] ^ p[nxt(i)];
        return sum;
    }

    // 多边形的周长
    long double circle() const
    {
        long double sum = 0;
        for (size_t i = 0; i < p.size(); i++)
            sum += p[i].dis(p[nxt(i)]);
        return sum;
    }
};
using Polygon = polygon<point_type>;

例题

计算几何spj hacker

题解

考察\(NAN\)的性质

显然我们构造出\(a / b=NAN\)即可，因为\(NAN > x,x为任何数=false\)

直接构造\(a = 0,b = 0\)即可

void solve()
{
    cout << 0 << " " << 0 << endl;
}

Winding Number

\(3 \leq n \leq 5000,1 \leq m \leq 5000\)

题解

如果把给你的点看作是多边形的顶点

那么每次询问就可以转化为：询问一个点是否在多边形内部

运用光线投射法在回转数法上的拓展即可

复杂度：\(O(nm)\)

const int N = 2e5 + 10, M = 4e5 + 10;

const double eps = 1e-9;

// 点与向量
template <typename T>
struct Point
{
    T x, y;
    bool operator==(const Point &a) const
    {
        return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
    }
    bool operator<(const Point &a) const
    {
        if (fabs(x - a.x) <= eps)
            return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const Point &a) const
    {
        return !(*this < a || *this == a);
    }
    Point operator+(const Point &a) const
    {
        return {x + a.x, y + a.y};
    }
    Point operator-(const Point &a) const
    {
        return {x - a.x, y - a.y};
    }
    Point operator-() const
    {
        return {-x, -y};
    }
    Point operator*(const T k) const
    {
        return {k * x, k * y};
    }
    Point operator/(const T k) const
    {
        return {x / k, y / k};
    }
    // 点积
    T operator*(const Point &a) const
    {
        return x * a.x + y * a.y;
    }
    // 叉积
    T operator^(const Point &a) const
    {
        return x * a.y - y * a.x;
    }
    // to_left 测试
    int to_left(const Point &a) const
    {
        auto t = (*this) ^ a;
        return (t > eps) - (t < -eps);
    }
    // 模长的平方
    T quad_len() const
    {
        return (*this) * (*this);
    }
    // 两点距离的平方
    T quad_dis(const Point &a) const
    {
        return (a - (*this)).quad_len();
    }
    // 向量模长
    long double len() const
    {
        return sqrtl(quad_len());
    }
    // 两点距离
    long double dis(const Point &a) const
    {
        return sqrtl(quad_dis(a));
    }
    // 向量旋转
    Point rot(const long double rad) const
    {
        return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
    }
};

// 直线
template <typename T>
struct Line
{
    // p 为直线上的一点， v 是方向向量
    Point<T> p, v;
    bool operator==(const Line &a) const
    {
        return v.to_left(a.v) == 0 && v.to_left(a.p) == 0;
    }
    int to_left(const Point<T> &a) const
    {
        return v.to_left(a - p);
    }
    // 直线交点
    Point<T> inter(const Line &a) const
    {
        return p + ((a.v ^ (p - a.p)) / (v ^ a.v)) * v;
    }
    // 点到直线的距离
    long double dis(const Point<T> &a) const
    {
        return abs(v ^ (a - p)) / v.len();
    }
    // 点在直线上的投影
    Point<T> project(const Point<T> &a) const
    {
        return p + ((a - p) * v / (v * v)) * v;
    }
};

// 线段
template <typename T>
struct Segment
{
    Point<T> a, b;

    // 判断点是否在线段上
    // -1 代表点在线段端点处， 0 代表点不在线段上， 1 代表点严格在线段上
    int is_on(const Point<T> &p) const
    {
        // 点在端点处
        if (p == a || p == b)
            return -1;
        return (p - a).to_left(p - b) == 0 && (p - a) * (p - b) < -eps;
    }

    // 判断线段和直线是否相交
    // -1 直线经过线段端点, 0 线段和直线不相交, 1 线段和直线严格相交
    int is_inter(const Line<T> &line) const
    {
        if (line.toleft(a) == 0 || line.toleft(b) == 0)
            return -1;
        return line.toleft(a) != line.toleft(b);
    }

    // 判断两线段是否相交
    // -1 在某一线段端点处相交, 0 两线段不相交, 1 两线段严格相交
    int is_inter(const Segment<T> &s) const
    {
        if (is_on(s.a) || is_on(s.b) || s.is_on(a) || s.is_on(b))
            return -1;
        // 跨立实验
        const Line<T> l{a, b - a}, ls{s.a, s.b - s.a};
        return l.toleft(s.a) * l.toleft(s.b) == -1 && ls.toleft(a) * ls.toleft(b) == -1;
    }
};

// 多边形
template <typename T>
struct Polygon
{
    vector<Point<T>> p; // 以逆时针顺序存储

    size_t nxt(const size_t i) const { return i == p.size() - 1 ? 0 : i + 1; }
    size_t pre(const size_t i) const { return i == 0 ? p.size() - 1 : i - 1; }

    // 回转数
    // 返回值第一项表示点是否在多边形边上
    // 对于狭义多边形，回转数为 0 表示点在多边形外，否则点在多边形内
    pair<bool, int> winding(const Point<T> &a) const
    {
        int cnt = 0;
        for (size_t i = 0; i < p.size(); i++)
        {
            const Point<T> u = p[i], v = p[nxt(i)];
            // 点在多边形上
            if (abs((a - u) ^ (a - v)) <= eps && (a - u) * (a - v) <= eps)
                return {true, 0};
            if (abs(u.y - v.y) <= eps)
                continue;
            const Line<T> uv = {u, v - u};
            // 保证 u 和 v 所连成的线段能被从点a 射出的射线击中
            if (u.y < v.y - eps && uv.to_left(a) <= 0)
                continue;
            if (u.y > v.y + eps && uv.to_left(a) >= 0)
                continue;
            if (u.y < a.y - eps && v.y >= a.y - eps)
                cnt++;
            if (u.y >= a.y - eps && v.y < a.y - eps)
                cnt--;
        }
        return {false, cnt};
    }

    // 多边形面积的两倍
    // 可用于判断点的存储顺序是顺时针或逆时针
    T area() const
    {
        T sum = 0;
        for (size_t i = 0; i < p.size(); i++)
            sum += p[i] ^ p[nxt(i)];
        return sum;
    }

    // 多边形的周长
    long double circle() const
    {
        long double sum = 0;
        for (size_t i = 0; i < p.size(); i++)
            sum += p[i].dis(p[nxt(i)]);
        return sum;
    }
};

int n, q;
vector<Point<int>> vec;

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        int x, y;
        cin >> x >> y;
        vec.push_back({x, y});
    }
    Polygon<int> poly;
    poly.p = vec;
    cin >> q;
    while (q--)
    {
        int x, y;
        cin >> x >> y;
        auto [flag, cnt] = poly.winding({x, y});
        if (flag)
            cout << "EDGE" << endl;
        else
            cout << cnt << endl;
    }
}

Mr. Main and Windmills

梅因先生乘火车从一个城市到另一个城市，经过一片到处是风车的平原。火车沿直线行驶。风车是用于风力发电的机器。它的风扇叶片在风吹的时候旋转。从他的角度看，五颜六色的风车从左到右排列在地平线上。

随着火车的行驶，从他的视角看，风车的排列顺序也在不断变化。风车原来在另一个的左边/右边，后来移到了右边/左边;根据风车的坐标，请找出他在观察第\(h\)个风车与其他风车交换顺序的第\(k\)次时的坐标。

可以保证，给定的任何三个点，即城市和风车，都不是共线的，而且所有的风车都在火车行驶路线的同一侧。

题解

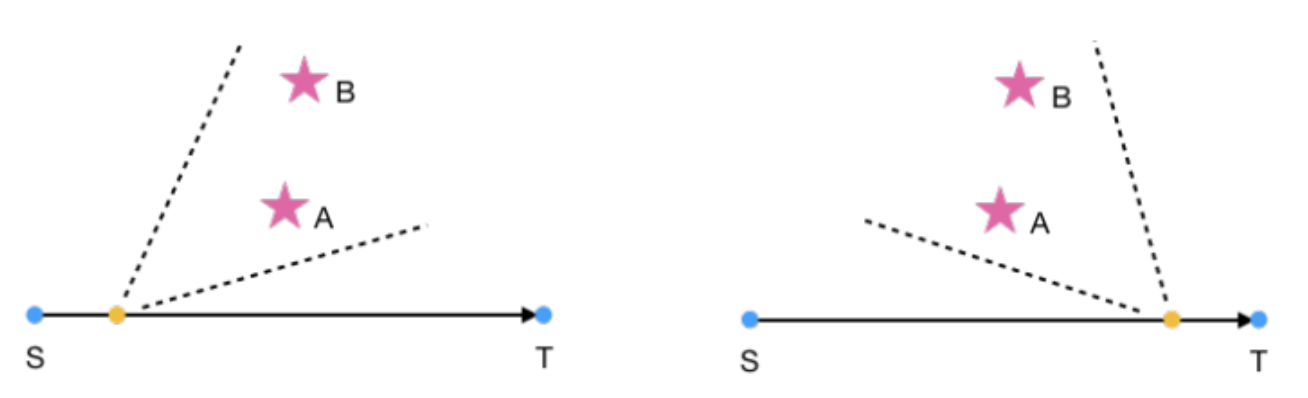
容易发现第\(h\)个风车与其他风车交换顺序的位置一定是线段\(ST\)和直线\(AB\)的交点

所以一个朴素的想法就是求出所有交点后排序即可

但是由于直接求交点会存在精度误差，所以我们应该先判断直线和线段有无交点，判断方法：两次\(to\_left\)测试

然后排序的话需要按照距离起点\(S\)的距离大小进行升序排列

const int N = 1e3 + 10, M = 4e5 + 10;

const double eps = 1e-8;

// 点与向量
template <typename T>
struct Point
{
    T x, y;
    bool operator==(const Point &a) const
    {
        return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
    }
    bool operator<(const Point &a) const
    {
        if (fabs(x - a.x) <= eps)
            return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const Point &a) const
    {
        return !(*this < a || *this == a);
    }
    Point operator+(const Point &a) const
    {
        return {x + a.x, y + a.y};
    }
    Point operator-(const Point &a) const
    {
        return {x - a.x, y - a.y};
    }
    Point operator-() const
    {
        return {-x, -y};
    }
    Point operator*(const T k) const
    {
        return {k * x, k * y};
    }
    Point operator/(const T k) const
    {
        return {x / k, y / k};
    }
    // 点积
    T operator*(const Point &a) const
    {
        return x * a.x + y * a.y;
    }
    // 叉积
    T operator^(const Point &a) const
    {
        return x * a.y - y * a.x;
    }
    // to_left 测试
    int to_left(const Point &a) const
    {
        auto t = (*this) ^ a;
        return (t > eps) - (t < -eps);
    }
    // 模长的平方
    T quad_len() const
    {
        return (*this) * (*this);
    }
    // 两点距离的平方
    T quad_dis(const Point &a) const
    {
        return (a - (*this)).quad_len();
    }
    // 向量模长
    long double len() const
    {
        return sqrtl(quad_len());
    }
    // 两点距离
    long double dis(const Point &a) const
    {
        return sqrtl(quad_dis(a));
    }
    // 向量旋转
    Point rot(const long double rad) const
    {
        return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
    }
};

// 直线
template <typename T>
struct Line
{
    // p 为直线上的一点， v 是方向向量
    Point<T> p, v;
    bool operator==(const Line &a) const
    {
        return v.to_left(a.v) == 0 && v.to_left(a.p) == 0;
    }
    int to_left(const Point<T> &a) const
    {
        return v.to_left(a - p);
    }
    // 直线交点
    Point<T> inter(const Line &a) const
    {
        return p + v * ((a.v ^ (p - a.p)) / (v ^ a.v));
    }
    // 点到直线的距离
    long double dis(const Point<T> &a) const
    {
        return abs(v ^ (a - p)) / v.len();
    }
    // 点在直线上的投影
    Point<T> project(const Point<T> &a) const
    {
        return p + v * ((a - p) * v / (v * v));
    }
};

#define double long double
int n, q;
Point<double> st, ed;
Point<double> p[N];

void solve()
{
    cin >> n >> q;
    cin >> st.x >> st.y >> ed.x >> ed.y;
    // Segment<double> seg = {st, ed};
    for (int i = 1; i <= n; ++i)
        cin >> p[i].x >> p[i].y;
    while (q--)
    {
        int h, k;
        cin >> h >> k;
        vector<Point<double>> vec;
        for (int i = 1; i <= n; ++i)
        {
            if (i == h)
                continue;
            Line<double> line = {p[h], p[i] - p[h]};
            // 先通过to_left测试判断直线和线段有无交点，如果有交点的话求交点
            if (line.to_left(st) * line.to_left(ed) <= 0)
            {
                Point<double> inter = line.inter({st, st - ed});
                vec.push_back(inter);
            }
        }
        sort(all(vec), [](Point<double> a, Point<double> b)
             { return st.dis(a) < st.dis(b); });
        if (vec.size() < k)
            cout << -1 << endl;
        else
            cout << fixed << setprecision(9) << vec[k - 1].x << " " << vec[k - 1].y << endl;
    }
}

Operation Love

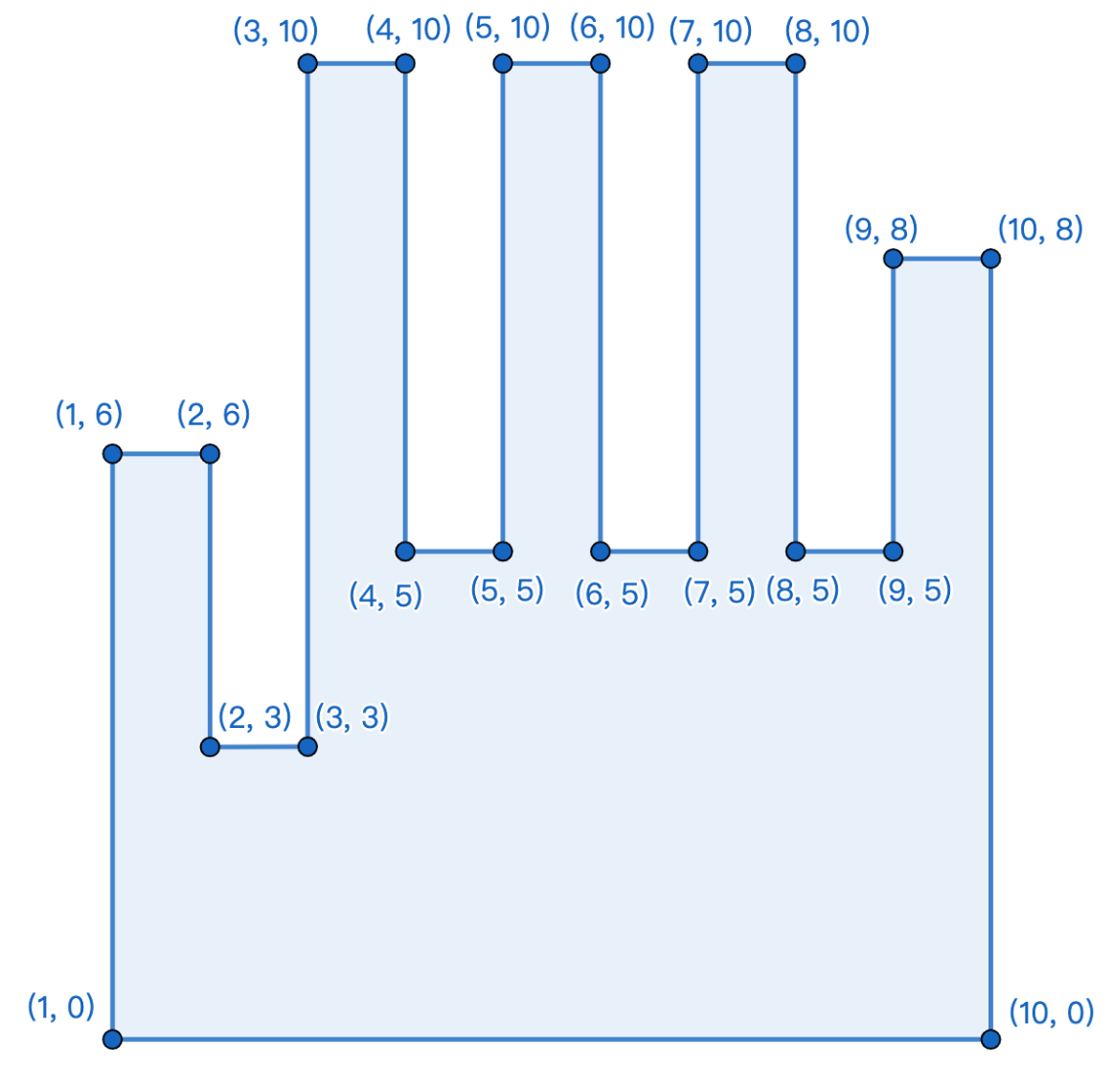
给定一只右手的样子，规定左手与右手对称，逆时针或顺时针给定\(20\)个点组成手，判断这是左手还是右手

题解

遍历每条边，找到长度为\(9\)的边

利用\(to\_left\)测试判断逆时针或顺时针

比较该边的两条邻边大小即可

const int N = 2e5 + 10, M = 4e5 + 10;

int n = 20;
using point_type = long double;

// 点与向量
template <typename T>
struct point
{
    T x, y;
    bool operator==(const point &a) const
    {
        return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
    }
    bool operator<(const point &a) const
    {
        if (fabs(x - a.x) <= eps)
            return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const point &a) const
    {
        return !(*this < a || *this == a);
    }
    point operator+(const point &a) const
    {
        return {x + a.x, y + a.y};
    }
    point operator-(const point &a) const
    {
        return {x - a.x, y - a.y};
    }
    point operator-() const
    {
        return {-x, -y};
    }
    point operator*(const T k) const
    {
        return {k * x, k * y};
    }
    point operator/(const T k) const
    {
        return {x / k, y / k};
    }
    // 点积
    T operator*(const point &a) const
    {
        return x * a.x + y * a.y;
    }
    // 叉积
    T operator^(const point &a) const
    {
        return x * a.y - y * a.x;
    }
    // to_left 测试
    int to_left(const point &a) const
    {
        auto t = (*this) ^ a;
        return (t > eps) - (t < -eps);
    }
    // 模长的平方
    T quad_len() const
    {
        return (*this) * (*this);
    }
    // 两点距离的平方
    T quad_dis(const point &a) const
    {
        return (a - (*this)).quad_len();
    }
    // 向量模长
    long double len() const
    {
        return sqrtl(quad_len());
    }
    // 两点距离
    long double dis(const point &a) const
    {
        return sqrtl(quad_dis(a));
    }
    // 向量旋转
    point rot(const long double rad) const
    {
        return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
    }
};
using Point = point<point_type>;

// 直线
template <typename T>
struct line
{
    // p 为直线上的一点， v 是方向向量
    point<T> p, v;
    bool operator==(const line &a) const
    {
        return v.to_left(a.v) == 0 && v.to_left(a.p) == 0;
    }
    int to_left(const point<T> &a) const
    {
        return v.to_left(a - p);
    }
    // 直线交点
    point<T> inter(const line &a) const
    {
        return p + v * ((a.v ^ (p - a.p)) / (v ^ a.v));
    }
    // 点到直线的距离
    long double dis(const point<T> &a) const
    {
        return abs(v ^ (a - p)) / v.len();
    }
    // 点在直线上的投影
    point<T> project(const point<T> &a) const
    {
        return p + v * ((a - p) * v / (v * v));
    }
};
using Line = line<point_type>;

Point p[25];

void solve()
{
    for (int i = 1; i <= n; ++i)
        cin >> p[i].x >> p[i].y;
    for (int i = 1; i <= n; ++i)
    {
        int nxt = i + 1;
        if (nxt == n + 1)
            nxt = 1;
        if (p[i].dis(p[nxt]) >= 9 - eps && p[i].dis(p[nxt]) <= 9 + eps)
        {
            int cnt0 = 0, cnt1 = 0;
            for (int j = 1; j <= n; ++j)
            {
                if (i == j || nxt == j)
                    continue;
                int tmp = (p[nxt] - p[i]).to_left(p[j] - p[i]);
                if (tmp < 0)
                    cnt0++;
                else if (tmp > 0)
                    cnt1++;
            }
            if (cnt0 == 18) // 顺时针给出
            {
                int j = nxt + 1;
                if (j == n + 1)
                    j = 1;
                int pre = i - 1;
                if (pre == 0)
                    pre = n;
                if (p[pre].quad_dis(p[i]) > p[nxt].quad_dis(p[j]))
                    cout << "right" << endl;
                else
                    cout << "left" << endl;
                return;
            }
            else if (cnt1 == 18) // 逆时针给出
            {
                int j = nxt + 1;
                if (j == n + 1)
                    j = 1;
                int pre = i - 1;
                if (pre == 0)
                    pre = n;
                if (p[pre].quad_dis(p[i]) > p[nxt].quad_dis(p[j]))
                    cout << "left" << endl;
                else
                    cout << "right" << endl;
                return;
            }
        }
    }
}

Magic Rabbit

给定\(3\)瓶溶液，每瓶溶液中物质\(A、B\)的比例分别为\((a_1,b_1),(a_2,b_2),(a_3,b_3)\)

\(q\)次询问，每次询问给定物质\(A、B\)的比例\((x,y)\)，询问是否能用上述三瓶溶液配制出\((x,y)\)的溶液

题解

我们考虑将问题转化一下

首先我们想知道\((a_1,b_1)\)和\((a_2,b_2)\)能够配制出什么比例的溶液

令\(\lambda_1\)为\(1\)号瓶使用的量，\(\lambda_2\)为\(2\)号瓶使用的量

则混合溶液中物质\(A\)的含量为\(\lambda_1a_1 + \lambda_2a_2\)，物质\(B\)的含量为\(\lambda_1b_1 + \lambda_2b_2\)

混合溶液中物质\(A\)的比例为\(\frac{\lambda_1a_1 + \lambda_2a_2}{\lambda_1+\lambda_2}\)，物质\(B\)的比例为\(\frac{\lambda_1b_1 + \lambda_2b_2}{\lambda_1+\lambda_2}\)

令\(\lambda = \frac{\lambda_1}{\lambda_1+\lambda_2},\lambda \in[0,1]\)，则：

\[\frac{\lambda_1a_1 + \lambda_2a_2}{\lambda_1+\lambda_2} = \lambda a_1 + (1 - \lambda)a_2\\ \frac{\lambda_1b_1 + \lambda_2b_2}{\lambda_1+\lambda_2} = \lambda b_1 + (1 - \lambda)b_2\\ \lambda (\left[ \matrix{ a_1\\ b_1\\ } \right] - \left[ \matrix{ a_2\\ b_2\\ } \right]) + \left[ \matrix{ a_2\\ b_2\\ } \right] \]

显然\((a_1,b_1)\)和\((a_2,b_2)\)能够配制出的溶液一定是两个点所连成的线段中的所有点

那么对于加入第三瓶溶液来说，可以配制的溶液在二维平面上形成了一个三角形区域

只要\((x,y)\)位于三角形的内部或边界，则一定可以配制成功

那么只要进行\(3\)次\(to\_left\)测试即可

注意：三角形有可能退化成三点共线，用叉积特判该情况即可

using point_type = long long;
// 点与向量
template <typename T>
struct point
{
    T x, y;
    bool operator==(const point &a) const
    {
        return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
    }
    bool operator<(const point &a) const
    {
        if (fabs(x - a.x) <= eps)
            return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const point &a) const
    {
        return !(*this < a || *this == a);
    }
    point operator+(const point &a) const
    {
        return {x + a.x, y + a.y};
    }
    point operator-(const point &a) const
    {
        return {x - a.x, y - a.y};
    }
    point operator-() const
    {
        return {-x, -y};
    }
    point operator*(const T k) const
    {
        return {k * x, k * y};
    }
    point operator/(const T k) const
    {
        return {x / k, y / k};
    }
    // 点积
    T operator*(const point &a) const
    {
        return x * a.x + y * a.y;
    }
    // 叉积
    T operator^(const point &a) const
    {
        return x * a.y - y * a.x;
    }
    // to_left 测试
    int to_left(const point &a) const
    {
        auto t = (*this) ^ a;
        return (t > eps) - (t < -eps);
    }
    // 模长的平方
    T quad_len() const
    {
        return (*this) * (*this);
    }
    // 两点距离的平方
    T quad_dis(const point &a) const
    {
        return (a - (*this)).quad_len();
    }
    // 向量模长
    long double len() const
    {
        return sqrtl(quad_len());
    }
    // 两点距离
    long double dis(const point &a) const
    {
        return sqrtl(quad_dis(a));
    }
    // 向量旋转
    point rot(const long double rad) const
    {
        return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
    }
};
using Point = point<point_type>;

// 线段
template <typename T>
struct segment
{
    point<T> a, b;

    // 判断点是否在线段上
    // -1 代表点在线段端点处， 0 代表点不在线段上， 1 代表点严格在线段上
    int is_on(const point<T> &p) const
    {
        // 点在端点处
        if (p == a || p == b)
            return -1;
        return (p - a).to_left(p - b) == 0 && (p - a) * (p - b) < -eps;
    }
};
using Segment = segment<point_type>;

int q;
int a1, b1, a2, b2, a3, b3;

void solve()
{
    cin >> a1 >> b1 >> a2 >> b2 >> a3 >> b3;
    Point a = {a1, b1}, b = {a2, b2}, c = {a3, b3};
    Segment l1 = {a, b}, l2 = {b, c}, l3 = {a, c};
    cin >> q;
    while (q--)
    {
        int x, y;
        cin >> x >> y;
        Point p = {x, y};
        // 判断点是否爱线段上
        if (l1.is_on(p) || l2.is_on(p) || l3.is_on(p))
            cout << "YES" << endl;
        else
        {
            // // 特判三点共线的情况
            if (((b - a) ^ (c - a)) == 0)
            {
                cout << "NO" << endl;
                continue;
            }
            if ((b - a).to_left(p - a) == -1 && (c - b).to_left(p - b) == -1 && (a - c).to_left(p - c) == -1 ||
                (b - a).to_left(p - a) == 1 && (c - b).to_left(p - b) == 1 && (a - c).to_left(p - c) == 1)
                cout << "YES" << endl;
            else
                cout << "NO" << endl;
        }
    }
}

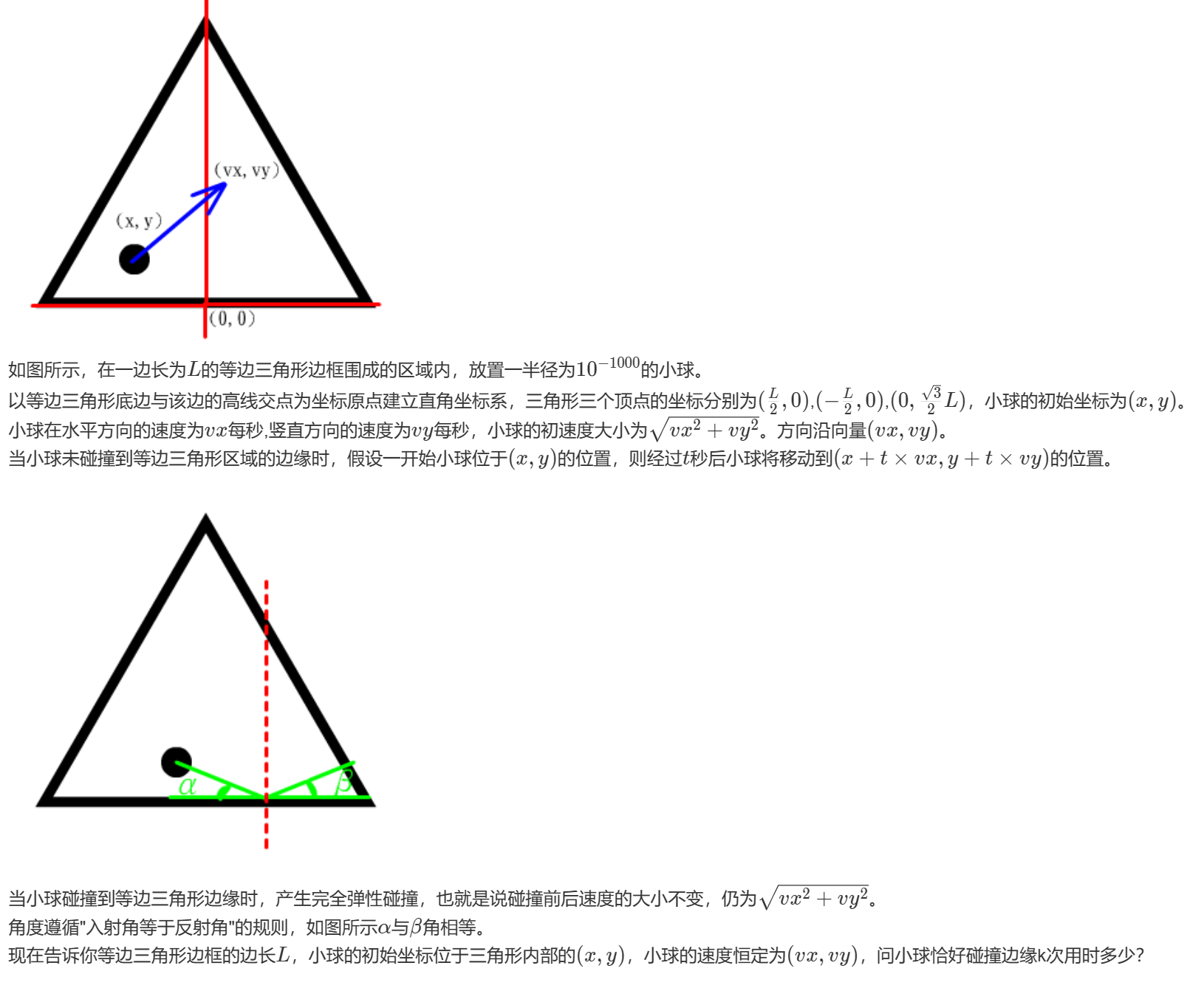
三角碰撞(Triangle Collision)

题解

反射是一个经典的问题，我们考虑将这个问题进行转化

如果我们不把小球的碰撞当作反射，而是继续运动，那么会发生什么呢？

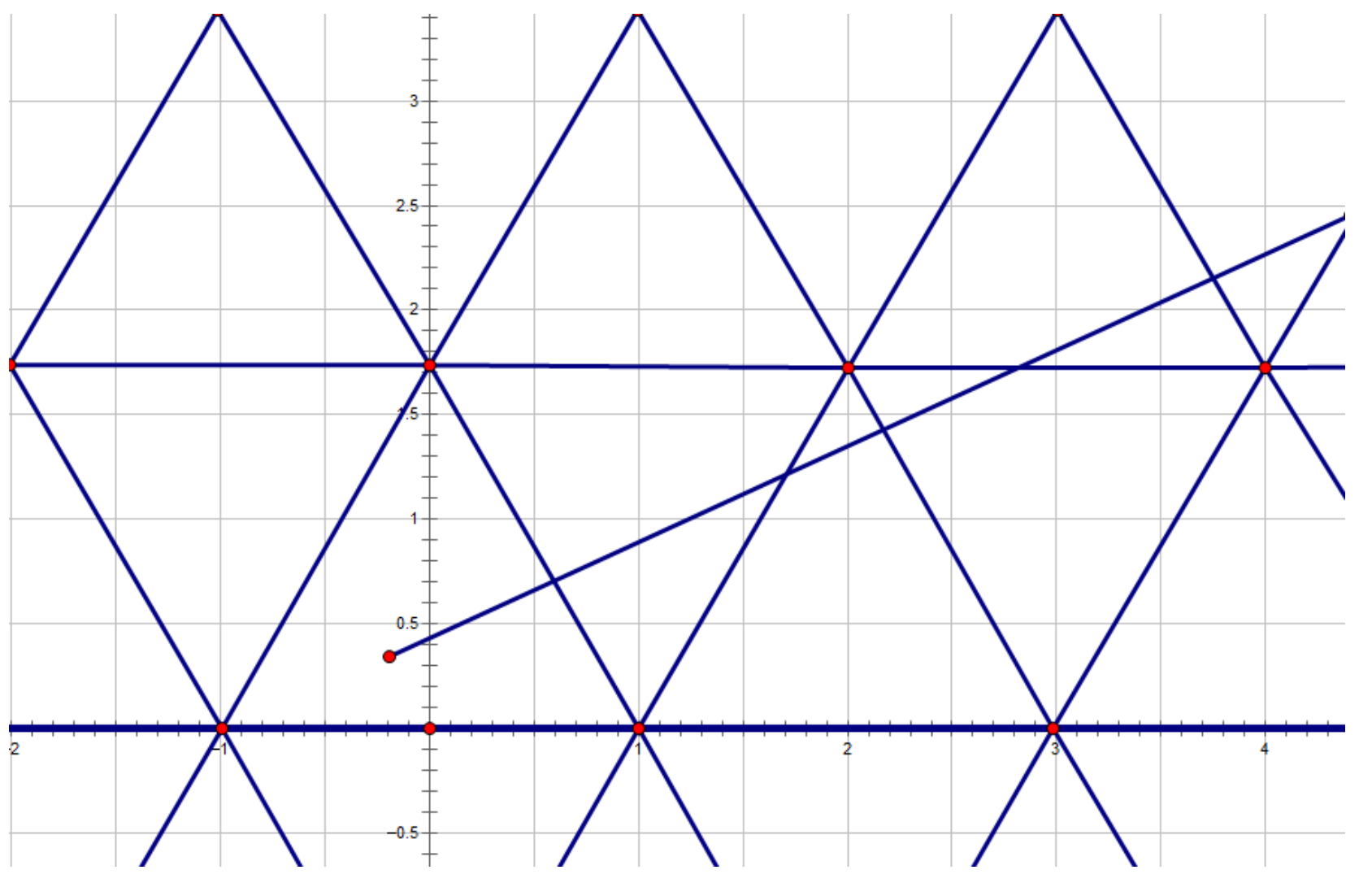
显然我们容易发现，我们只需要把平面拓展成由无数个等边三角形组成，那么反射几次的问题就转换成了：

从起点出发的一条直线，与其他直线交第\(k\)次时所花费的时间

那么显然我们可以二分时间

\(check\)的时候我们计算出与\(3\)种直线一共由多少个交点即可

那么现在的问题就是怎样快速知道有几个交点

假设时间为\(t\)，对于\(y = b\)这一类直线来说，在垂直方向上运动的距离\(s = v_y*t\)，而每条直线之间的距离为\(\frac{\sqrt{3}}{2}L\)，那么我们显然可以\(O(1)\)得到与\(y = b\)这类直线的交点个数，当然我们对于\(v_y\)的正负需要简单分类讨论一下

那对于其他两种直线\(y = \sqrt{3}x+b,y = -\sqrt{3}x + b\)来说呢？

这又是一个经典的问题：我们可以考虑旋转坐标系

比如说：对于方向向量\((v_x,v_y)\)来说，如果要计算和\(y = \sqrt{3}x+b\)的交点个数时，我们考虑将方向向量逆时针旋转\(120°\)

当旋转完之后，操作和第一种直线是一样的

const long double PI = acos(-1.0);

using point_type = long double;
// 点与向量
template <typename T>
struct point
{
    T x, y;
    bool operator==(const point &a) const
    {
        return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
    }
    bool operator<(const point &a) const
    {
        if (fabs(x - a.x) <= eps)
            return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const point &a) const
    {
        return !(*this < a || *this == a);
    }
    point operator+(const point &a) const
    {
        return {x + a.x, y + a.y};
    }
    point operator-(const point &a) const
    {
        return {x - a.x, y - a.y};
    }
    point operator-() const
    {
        return {-x, -y};
    }
    point operator*(const T k) const
    {
        return {k * x, k * y};
    }
    point operator/(const T k) const
    {
        return {x / k, y / k};
    }
    // 点积
    T operator*(const point &a) const
    {
        return x * a.x + y * a.y;
    }
    // 叉积
    T operator^(const point &a) const
    {
        return x * a.y - y * a.x;
    }
    // to_left 测试
    int to_left(const point &a) const
    {
        auto t = (*this) ^ a;
        return (t > eps) - (t < -eps);
    }
    // 模长的平方
    T quad_len() const
    {
        return (*this) * (*this);
    }
    // 两点距离的平方
    T quad_dis(const point &a) const
    {
        return (a - (*this)).quad_len();
    }
    // 向量模长
    long double len() const
    {
        return sqrtl(quad_len());
    }
    // 两点距离
    long double dis(const point &a) const
    {
        return sqrtl(quad_dis(a));
    }
    // 向量逆时针旋转
    point rotate(const long double rad) const
    {
        return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
    }
};
using Point = point<point_type>;

// 直线
template <typename T>
struct line
{
    // p 为直线上的一点， v 是方向向量
    point<T> p, v;
    bool operator==(const line &a) const
    {
        return v.to_left(a.v) == 0 && v.to_left(a.p) == 0;
    }
    int to_left(const point<T> &a) const
    {
        return v.to_left(a - p);
    }
    // 直线交点
    point<T> inter(const line &a) const
    {
        return p + v * ((a.v ^ (p - a.p)) / (v ^ a.v));
    }
    // 点到直线的距离
    long double dis(const point<T> &a) const
    {
        return abs(v ^ (a - p)) / v.len();
    }
    // 点在直线上的投影
    point<T> project(const point<T> &a) const
    {
        return p + v * ((a - p) * v / (v * v));
    }
};
using Line = line<point_type>;

int k;
long double L, x, y, h, vx, vy, d1, d2, d3;
Point v1, v2, v3;

bool check(long double mid)
{
    int cnt1 = 0, cnt2 = 0, cnt3 = 0;
    long double s = v1.y * mid;
    if (s > 0)
    {
        s -= (h - d1);
        cnt1 = (int)ceill(s / h);
    }
    else if (s < 0)
    {
        s = fabs(s);
        s -= d1;
        cnt1 = (int)ceill(s / h);
    }

    s = v2.y * mid;
    if (s > 0)
    {
        s -= (h - d2);
        cnt2 = (int)ceill(s / h);
    }
    else if (s < 0)
    {
        s = fabs(s);
        s -= d2;
        cnt2 = (int)ceill(s / h);
    }

    s = v3.y * mid;
    if (s > 0)
    {
        s -= (h - d3);
        cnt3 = (int)ceill(s / h);
    }
    else if (s < 0)
    {
        s = fabs(s);
        s -= d3;
        cnt3 = (int)ceill(s / h);
    }
    return cnt1 + cnt2 + cnt3 >= k;
}

void solve()
{
    cin >> L >> x >> y >> vx >> vy >> k;
    h = sqrtl(3) / 2.0 * L;
    v1 = {vx, vy};
    v2 = v1.rotate(2.0 * PI / 3);
    v3 = v1.rotate(-2.0 * PI / 3);
    Point p = {x, y};
    Point A = {-L / 2.0, 0};
    Point B = {L / 2.0, 0};
    Point C = {0, h};
    Line ab = {A, B - A};
    Line bc = {B, C - B};
    Line ca = {C, A - C};
    d1 = ab.dis(p);
    d2 = ca.dis(p);
    d3 = bc.dis(p);
    long double l = 0, r = 1e10;
    while (r - l >= eps)
    {
        long double mid = (l + r) / 2;
        if (check(mid))
            r = mid;
        else
            l = mid;
    }
    cout << fixed << setprecision(8) << r << endl;
}

posted @ 2023-08-23 21:59 Zeoy_kkk 阅读(6) 评论(0) 编辑收藏举报

刷新页面返回顶部

Zeoy-kkk

二维基础

前置知识

点

向量

点积

叉积

\(to\_left\)测试

向量旋转

线段

判断点是否在线段上

判断两个线段是否相交

直线

点到直线的距离

点在直线上的投影

两直线的交点

多边形

多边形的面积

判断点是否在多边形内部

模板

例题

计算几何spj hacker

题解

Winding Number

题解

Mr. Main and Windmills

题解

Operation Love

题解

Magic Rabbit

题解

三角碰撞(Triangle Collision)

题解

公告