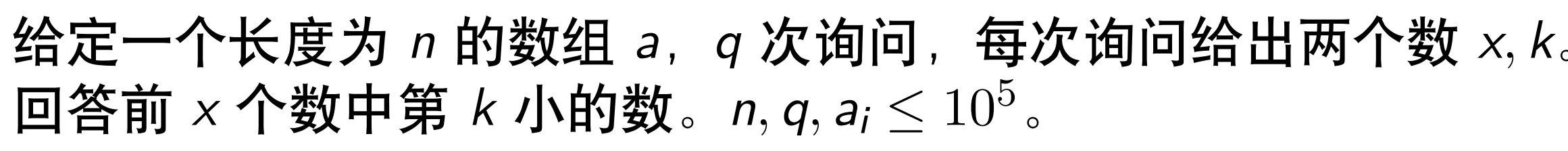线段树

普通线段树

const int N = 2e5 + 10;
int a[N];
struct info
{
    int sum, maxx, minn;
};
struct node
{
    int lazy, len;
    info val;
} seg[N << 2];
info operator+(const info &a, const info &b)
{
    info c;
    c.sum = a.sum + b.sum;
    c.maxx = max(a.maxx, b.maxx);
    c.minn = min(a.minn, b.minn);
    return c;
}
void settag(int id, int tag)
{
    seg[id].val.sum += seg[id].len * tag;
    seg[id].lazy += tag;
}
void up(int id)
{
    seg[id].val = seg[id << 1].val + seg[id << 1 | 1].val;
}
void down(int id)
{
    if (seg[id].lazy == 0)
        return;
    settag(id << 1, seg[id].lazy);
    settag(id << 1 | 1, seg[id].lazy);
    seg[id].lazy = 0;
}
void build(int id, int l, int r)
{
    seg[id].len = r - l + 1;
    if (l == r)
    {
        seg[id].val.sum = a[l];
        seg[id].lazy = 0;
        return;
    }
    int mid = (l + r) >> 1;
    build(id << 1, l, mid);
    build(id << 1 | 1, mid + 1, r);
    up(id);
}
void change(int id, int l, int r, int x, int val)
{
    if (l == r)
    {
        seg[id].val.sum += val;
        return;
    }
    down(id);
    int mid = (l + r) >> 1;
    if (x <= mid)
        change(id << 1, l, mid, x, val);
    else if (x > mid)
        change(id << 1 | 1, mid + 1, r, x, val);
    up(id);
}
void modify(int id, int l, int r, int ql, int qr, int val)
{
    if (ql <= l && r <= qr)
    {
        settag(id, val);
        return;
    }
    down(id);
    int mid = (l + r) >> 1;
    if (qr <= mid)
        modify(id << 1, l, mid, ql, qr, val);
    else if (ql > mid)
        modify(id << 1 | 1, mid + 1, r, ql, qr, val);
    else
    {
        modify(id << 1, l, mid, ql, qr, val);
        modify(id << 1 | 1, mid + 1, r, ql, qr, val);
    }
    up(id);
}
info query(int id, int l, int r, int ql, int qr)
{
    if (ql <= l && r <= qr)
    {
        return seg[id].val;
    }
    down(id);
    int mid = (l + r) >> 1;
    if (qr <= mid)
        return query(id << 1, l, mid, ql, qr);
    else if (ql > mid)
        return query(id << 1 | 1, mid + 1, r, ql, qr);
    else
        return query(id << 1, l, mid, ql, qr) + query(id << 1 | 1, mid + 1, r, ql, qr);
}

可持久化权值线段树（主席树）

前置知识1

题解：扫描线 + 在权值线段树树上二分 / 在权值树状数组上倍增

从前往后遍历询问

在值域上维护权值线段树

线段树上二分即可

前置知识2

题解：离散化 + 权值线段树

操作数只有\(1e5\)，所以离散化后值域不超过\(1e5\)，直接权值线段树维护即可

查询时线段树上区间询问即可

题解：扫描线 + 离散化 + 权值线段树

从第一个人开始往后扫描

对于每个人利用权值线段树维护，然后利用\(vector\)记录吃的食物，当一个人的查询结束的时候，对这个人的操作在线段树上进行撤销即可

这样既保证了每个人的独立也保证了空间的大小，只需要开一颗权值线段树

动态开点

强制在线

那么我们无法对每个人都开一个权值线段树，因为空间不够

所以我们需要动态开点，用了再开，不用就不开，如果动态开点的话我们就要舍弃原本线段树的编号规则

我们发现操作数最多为\(1e5\)次，所以最多只有\(1e5\)次单点修改，我们不妨给每个人一个根节点，每次单点修改只会影响一条链，且链长最长为 \(log\ m\)，所以空间肯定是够的

可持久化线段树的介绍

什么是可持久化？简单来说就是记录每一个历史版本

形象的说。我要砍你 \(100\) 刀，每砍一刀就给你拍一张照片。结束的时候我有了 \(101\) 张照片。把这些照片订成一本相册，这本相册记录了整个过程，可以随时取出砍了任意刀的照片来查看当时具体的情况。这就是可持久化的。

可持久化线段树就是把线段树可持久化，还有很多其他的数据结构也可以可持久化，例如：\(Dsu\)，\(Trie\) 等。

模板

int rt[N * 66], lson[N * 66], rson[N * 66], sum[N * 66], idx;

void up(int id)
{
    sum[id] = sum[lson[id]] + sum[rson[id]];
}

void insert(int &rt, int pre, int l, int r, int x)
{
    rt = ++idx;           // 动态开点
    lson[rt] = lson[pre]; // 复制前一个版本的信息
    rson[rt] = rson[pre];
    sum[rt] = sum[pre];
    if (l == r)
    {
        sum[rt]++;
        return;
    }
    int mid = l + r >> 1;
    if (x <= mid)
        insert(lson[rt], lson[pre], l, mid, x);
    else
        insert(rson[rt], rson[pre], mid + 1, r, x);
    up(rt);
}

// 查询区间第k大
int query(int rt, int pre, int l, int r, int k)
{
    if (l == r)
        return l;
    int cnt = sum[lson[rt]] - sum[lson[pre]];
    int mid = l + r >> 1;
    if (cnt >= k)
        return query(lson[rt], lson[pre], l, mid, k);
    else
        return query(rson[rt], rson[pre], mid + 1, r, k - cnt);
}

例1·区间第\(k\)小

题解：可持久化线段树 + 线段树上二分

如果我们每次可以快速获得 \([l,r]\) 组成的子数组所建立的权值线段树，那么每次询问只要在这棵权值线段树上二分即可

考虑维护一棵初始为空的权值线段树，从左到右依次加入每个数，每次加入会改变这棵权值线段树，我们动态开点，并且设法保存每棵线段树。

形式上说，保存 n 棵线段树，第 i 棵线段树上的信息就是考虑数组中前 i 个数所建的线段树。

如何得到 [l,r] 组成的权值线段树？只要将第 r 棵树减去第 l − 1 棵树就行啦。

但是 n 棵线段树显然是存不下的。但是发现第 i 棵线段树与第 i − 1 棵线段树的区别至多只有一条链的区别。所以可以偷过来。

const int N = 2e5 + 10, M = 4e5 + 10;

int n, q;
int a[N];
vector<int> vec;
int rt[N * 66], lson[N * 66], rson[N * 66], sum[N * 66], idx;

void up(int id)
{
    sum[id] = sum[lson[id]] + sum[rson[id]];
}

void change(int &rt, int pre, int l, int r, int x)
{
    rt = ++idx;           // 动态开点
    lson[rt] = lson[pre]; // 复制前一个版本的信息
    rson[rt] = rson[pre];
    sum[rt] = sum[pre];
    if (l == r)
    {
        sum[rt]++;
        return;
    }
    int mid = l + r >> 1;
    if (x <= mid)
        change(lson[rt], lson[pre], l, mid, x);
    else
        change(rson[rt], rson[pre], mid + 1, r, x);
    up(rt);
}

// 查询区间第k大
int query(int rt, int pre, int l, int r, int k)
{
    if (l == r)
        return l;
    int cnt = sum[lson[rt]] - sum[lson[pre]];
    int mid = l + r >> 1;
    if (cnt >= k)
        return query(lson[rt], lson[pre], l, mid, k);
    else
        return query(rson[rt], rson[pre], mid + 1, r, k - cnt);
}

int find(int x)
{
    return lower_bound(all(vec), x) - vec.begin() + 1;
}

void solve()
{
    cin >> n >> q;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        vec.push_back(a[i]);
    }

    // 离散化
    sort(all(vec));
    vec.erase(unique(all(vec)), vec.end());

    for (int i = 1; i <= n; ++i)
        change(rt[i], rt[i - 1], 1, n, find(a[i]));

    while (q--)
    {
        int l, r, k;
        cin >> l >> r >> k;
        cout << vec[query(rt[r], rt[l - 1], 1, n, k) - 1] << endl;
    }
}

例2·树上路径第\(k\)小

题解

const int N = 1e5 + 10, M = 4e5 + 10;

int n, q;
vector<pii> g[N];
int rt[N * 45], lson[N * 45], rson[N * 45], sum[N * 45], idx;
int fa[N][22];
int dep[N];

void up(int id)
{
    sum[id] = sum[lson[id]] + sum[rson[id]];
}

void change(int &rt, int pre, int l, int r, int x)
{
    rt = ++idx;           // 动态开点
    lson[rt] = lson[pre]; // 复制前一个版本的信息
    rson[rt] = rson[pre];
    sum[rt] = sum[pre];
    if (l == r)
    {
        sum[rt]++;
        return;
    }
    int mid = l + r >> 1;
    if (x <= mid)
        change(lson[rt], lson[pre], l, mid, x);
    else
        change(rson[rt], rson[pre], mid + 1, r, x);
    up(rt);
}

int query(int u, int v, int LCA, int l, int r, int k)
{
    if (l == r)
        return l;
    int cnt = sum[lson[u]] + sum[lson[v]] - 2 * sum[lson[LCA]];
    int mid = l + r >> 1;
    if (cnt >= k)
        return query(lson[u], lson[v], lson[LCA], l, mid, k);
    else
        return query(rson[u], rson[v], rson[LCA], mid + 1, r, k - cnt);
}

void dfs(int u, int par)
{
    dep[u] = dep[par] + 1;
    fa[u][0] = par;

    for (int i = 1; i <= 20; ++i)
        fa[u][i] = fa[fa[u][i - 1]][i - 1];

    for (auto [v, w] : g[u])
    {
        if (v == par)
            continue;
        change(rt[v], rt[u], 1, 1e5, w);
        dfs(v, u);
    }
}

int lca(int u, int v)
{
    if (dep[u] < dep[v])
        swap(u, v);
    for (int i = 20; i >= 0; --i)
    {
        if (dep[fa[u][i]] >= dep[v])
            u = fa[u][i];
    }
    if (u == v)
        return u;
    for (int i = 20; i >= 0; --i)
    {
        if (fa[u][i] != fa[v][i])
        {
            u = fa[u][i];
            v = fa[v][i];
        }
    }
    return fa[u][0];
}

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        g[i].clear();
    idx = 0;
    memset(rt, 0, sizeof rt);
    memset(lson, 0, sizeof lson);
    memset(rson, 0, sizeof rson);
    memset(sum, 0, sizeof sum);
    memset(fa, 0, sizeof fa);
    memset(dep, 0, sizeof dep);

    for (int i = 1, u, v, w; i < n; ++i)
    {
        cin >> u >> v >> w;
        g[u].push_back({v, w});
        g[v].push_back({u, w});
    }
    dfs(1, 0);
    cin >> q;
    while (q--)
    {
        int u, v;
        cin >> u >> v;
        int LCA = lca(u, v);
        int cnt = dep[u] - dep[LCA] + dep[v] - dep[LCA];
        if (cnt % 2 == 1)
        {
            int k = cnt / 2 + 1;
            cout << fixed << setprecision(1) << 1.0 * query(rt[u], rt[v], rt[LCA], 1, 1e5, k) << endl;
        }
        else
        {
            int k1 = cnt / 2;
            int k2 = cnt / 2 + 1;
            cout << fixed << setprecision(1) << (query(rt[u], rt[v], rt[LCA], 1, 1e5, k1) + query(rt[u], rt[v], rt[LCA], 1, 1e5, k2)) / 2.0 << endl;
        }
    }
}

例3·Hossam and Range Minimum Query

题解：可持久化前缀异或和 + 随机化

我们不妨可持久化前缀异或和

如果最终这段区间\([l,r]\)的异或和为0，代表全是偶数，否则一定有奇数存在，因为要最小的数，我们直接在线段树上二分时优先往左儿子的方向走

但是很有可能最终异或和为0，但是存在出现次数为奇数的情况，例如\(1,2,3\)的异或和为0，但是存在出现次数为奇数的情况

所以我们不妨将每一个\(a_i\)映射到一个大的\([1,2^{32} - 1]\)值域中

那么两个数异或和为0的概率为\(\frac{1}{2^{32}}\)

那么这样的话基本上不可能存在的异或和为0的情况

那么我们如何映射呢？

我们需要用到随机化中的随机数\(mt\_19937\)

const int N = 2e5 + 10, M = 4e5 + 10;

int n, q;
int a[N];
vector<int> vec;
mt19937 mt_rand(time(0));
int rt[N * 33], lson[N * 33], rson[N * 33], sum[N * 33], idx;
int rnd[N];
map<int, int> mp;

void up(int id)
{
    sum[id] = sum[lson[id]] ^ sum[rson[id]];
}

void change(int &rt, int pre, int l, int r, int x)
{
    rt = ++idx;           // 动态开点
    lson[rt] = lson[pre]; // 复制前一个版本的信息
    rson[rt] = rson[pre];
    sum[rt] = sum[pre];
    if (l == r)
    {
        sum[rt] ^= x;
        return;
    }
    int mid = l + r >> 1;
    if (x <= mid)
        change(lson[rt], lson[pre], l, mid, x);
    else
        change(rson[rt], rson[pre], mid + 1, r, x);
    up(rt);
}

int query(int rt, int pre, int l, int r)
{
    if (l == r)
        return l;
    int Lval = sum[lson[rt]] ^ sum[lson[pre]];
    int Rval = sum[rson[rt]] ^ sum[rson[pre]];
    int mid = l + r >> 1;
    if (Lval > 0)
        return query(lson[rt], lson[pre], l, mid);
    else if (Rval > 0)
        return query(rson[rt], rson[pre], mid + 1, r);
    else
        return 0;
}

int find(int x)
{
    return lower_bound(all(vec), x) - vec.begin() + 1;
}

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        vec.push_back(a[i]);
    }

    sort(all(vec));
    vec.erase(unique(all(vec)), vec.end());

    for (int i = 1; i <= n; ++i)
        a[i] = find(a[i]);

    int m = 0;
    for (int i = 1; i <= vec.size(); ++i)
    {
        rnd[i] = mt_rand();
        m = max(rnd[i], m);
    }
    m += 10;
    sort(rnd + 1, rnd + vec.size() + 1);

    for (int i = 1; i <= n; ++i)
    {
        mp[rnd[a[i]]] = vec[a[i] - 1];
        a[i] = rnd[a[i]];
    }

    for (int i = 1; i <= n; ++i)
        change(rt[i], rt[i - 1], 1, m, a[i]);

    cin >> q;
    int ans = 0;
    while (q--)
    {
        int l, r;
        cin >> l >> r;
        l = l ^ ans;
        r = r ^ ans;
        ans = query(rt[r], rt[l - 1], 1, m);
        if (ans != 0)
            ans = mp[ans];
        cout << ans << endl;
    }
}

posted @ 2023-07-10 01:49 Zeoy_kkk 阅读(8) 评论(0) 编辑收藏举报

刷新页面返回顶部

Zeoy-kkk

线段树

普通线段树

可持久化权值线段树（主席树）

前置知识1

题解：扫描线 + 在权值线段树树上二分 / 在权值树状数组上倍增

前置知识2

题解：离散化 + 权值线段树

题解：扫描线 + 离散化 + 权值线段树

动态开点

可持久化线段树的介绍

模板

例1·区间第\(k\)小

题解：可持久化线段树 + 线段树上二分

例2·树上路径第\(k\)小

题解

例3·Hossam and Range Minimum Query

题解：可持久化前缀异或和 + 随机化

公告