扫描线
- 扫描线能做什么?
- 扫描线实际上是一种思想,而不是一种数据结构,它是一种离线算法,他将事件点按照某种由你规定的顺序执行后得到答案,一般需要线段树或者树状数组维护,同时有时也需要离散化
- 扫描线一般运用在图形上面,它和它的字面意思十分相似,就是一条线在整个图上扫来扫去,它一般被用来解决矩形面积并,矩形周长并,以及二维数点等问题。
- 同样也可以将二维偏序问题转化为二维数点问题,例如逆序对问题
- 总而言之,扫描线的思路就是通过数据结构维护一维,暴力扫描模拟另一维
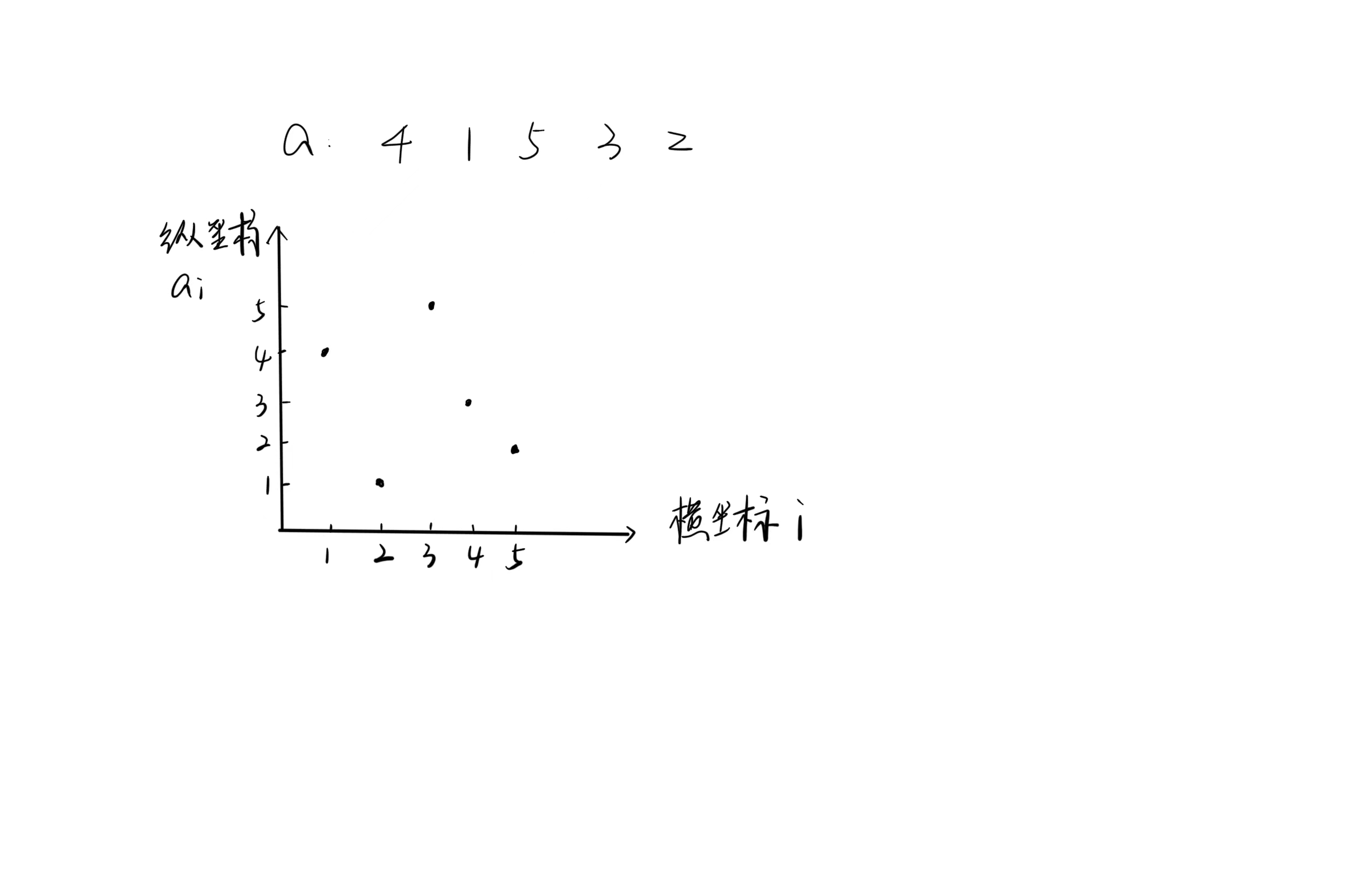
例1·二维数点问题
题解:扫描线思想 + 离散化 + 树状数组维护
- 如果\(n \leq 5000\),我们可以利用二维前缀和实现该问题
- 如果\(n \leq 2e5\),我们需要利用扫描线思想模拟二维前缀和来解决该问题
- 我们将图上的点分为初始点、查询点,每次查询都要分成4个查询点(借助二维前缀和的思想),初始点和查询点组成了事件点;
- 当然对于事件点,我们需要对横坐标\(x\)进行离散化,方便后面树状数组维护
- 我们不妨以\(y\)轴从下往上扫描,对于\(y\)值相同的点,我们应该先遍历初始点,再遍历查询点,防止查询的时候漏点,对于每个初始点我们在树状数组中将其横坐标\(x\)的位置 + 1,这样就算在\(x\)处存在一个点
- 那么每次遇到查询点\((x,y)\)的时候,\((1,1)-(x,y)\)矩形之间点的个数就是树状数组维护的前缀和
- 总结一下,我们用树状数组维护\(x\)轴,扫描\(y\)轴,同时注意事件点出现的顺序,先添加后查询
const int N = 8e5 + 10, M = 4e5 + 10;
int n, q;
pii p[N]; // 初始点
int c[N];
vector<array<int, 9>> qry; // 查询点
vector<array<int, 4>> eve; // 事件点:包括初始点和查询点
int ans[N][4];
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
if (x < N)
{
c[x] += val;
x += lowbit(x);
}
}
int get_sum(int x)
{
int res = 0;
while (x > 0)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int query(int l, int r)
{
return get_sum(r) - get_sum(l - 1);
}
void solve()
{
cin >> n >> q;
vector<int> vec;
// 添加初始点
for (int i = 1; i <= n; ++i)
{
cin >> p[i].first >> p[i].second;
vec.push_back(p[i].first);
}
// 添加查询点
for (int i = 1; i <= q; ++i)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
qry.push_back({x1 - 1, y1 - 1,
x2, y1 - 1,
x1 - 1, y2,
x2, y2,
i}); // 每个查询分为四个查询点
vec.push_back(x1 - 1);
vec.push_back(x2);
}
// 对坐标x进行离散化
sort(all(vec));
vec.erase(unique(all(vec)), vec.end());
// 将初始点转化为事件点,规定事件点的编号为-1
for (int i = 1; i <= n; ++i)
{
int pos = lower_bound(all(vec), p[i].first) - vec.begin() + 1;
eve.push_back({p[i].second, -1, pos, -1});
}
// 将查询点转化为事件点,规定查询点的编号为id > 0,即查询的顺序
for (auto &it : qry)
{
int x1 = it[0], y1 = it[1]; // 矩阵左下角
int x2 = it[2], y2 = it[3]; // 矩阵右下角
int x3 = it[4], y3 = it[5]; // 矩阵左上角
int x4 = it[6], y4 = it[7]; // 矩阵右上角
int id = it[8]; // 查询的编号
x1 = x3 = lower_bound(all(vec), x1) - vec.begin() + 1;
x2 = x4 = lower_bound(all(vec), x2) - vec.begin() + 1;
eve.push_back({y1, id, x1, 0}); // 将矩阵左上角的查询点转化为事件点
eve.push_back({y2, id, x2, 1});
eve.push_back({y3, id, x3, 2});
eve.push_back({y4, id, x4, 3});
}
// 扫描线
// 扫描线以y轴为轴向上扫描,在同一y值的情况下,以x升序的方式扫描,并且先扫描初始点,再扫描查询点,保证查询时没有数据遗漏
sort(all(eve));
for (auto &it : eve)
{
int id = it[1];
int x = it[2];
int pos = it[3];
if (id == -1) // 如果当前事件点为初始点
add(x, 1);
else // 如果当前事件点为查询点
ans[id][pos] = query(1, x);
}
for (int i = 1; i <= q; ++i)
{
cout << ans[i][3] - ans[i][1] - ans[i][2] + ans[i][0] << endl;
}
}
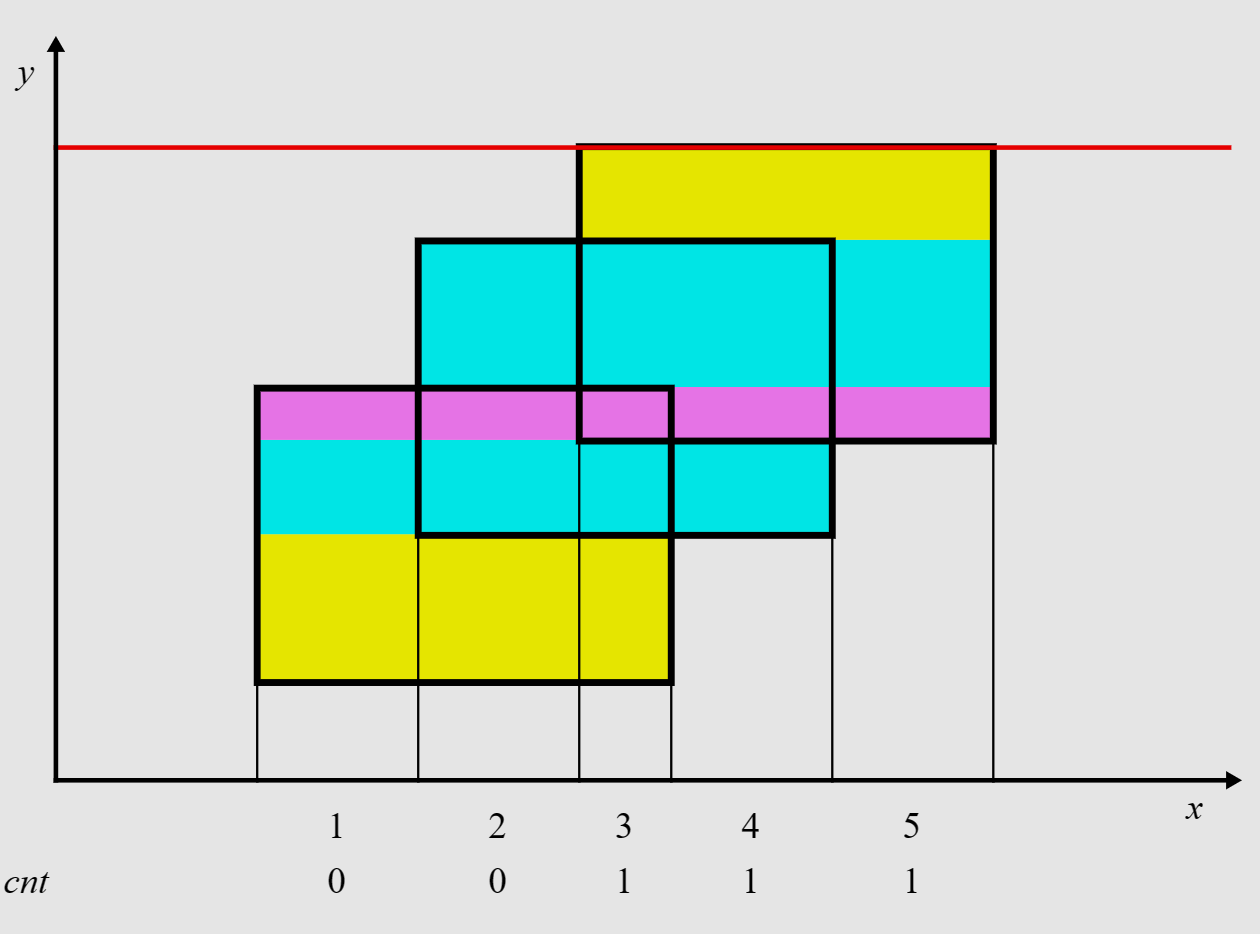
例2·矩形面积并
题解:扫描线 + 离散化 + 线段树
- 将每个矩形上下两条边分别设为出边和入边
- 对矩形左右两边的横坐标\(x\)进行离散化,方便线段树区间修改
- 以\(y\)轴升序进行扫描,当扫描到矩形的入边时,区间 + 1,当扫描到矩形的出边时,区间 - 1,注意我们需要计算面积贡献再区间修改
- 如何计算面积贡献:
- 对于高度我们完全可以维护一个\(preY\),那么矩形高度为\(y - preY\)
- 对于宽度,线段树额外维护最小值和最小值在整个区间中的出现次数,设区间总长度为\(len\),那么当最小值为0的时候说明有整个区间中有部分地方没有线段覆盖,设最小值出现次数为\(cnt\),则宽度为\(len - cnt\),否则宽度为\(len\)
const int N = 1e5 + 10, M = 4e5 + 10;
int n;
vector<int> vec;
array<int, 4> p[N];
vector<array<int, 4>> eve;
struct info
{
int mi, cnt; // 维护最小值和最小值出现的次数
};
struct node
{
int lazy;
info val;
} seg[N << 3];
info operator+(const info &a, const info &b)
{
info c;
c.mi = min(a.mi, b.mi);
if (a.mi < b.mi)
c.cnt = a.cnt;
else if (a.mi > b.mi)
c.cnt = b.cnt;
else
c.cnt = a.cnt + b.cnt;
return c;
}
void settag(int id, int tag)
{
seg[id].val.mi += tag;
seg[id].lazy += tag;
}
void up(int id)
{
seg[id].val = seg[id << 1].val + seg[id << 1 | 1].val;
}
void down(int id)
{
if (seg[id].lazy == 0)
return;
settag(id << 1, seg[id].lazy);
settag(id << 1 | 1, seg[id].lazy);
seg[id].lazy = 0;
}
void build(int id, int l, int r)
{
if (l == r)
{
seg[id].val.mi = 0;
seg[id].val.cnt = vec[r] - vec[r - 1];
seg[id].lazy = 0;
return;
}
int mid = (l + r) >> 1;
build(id << 1, l, mid);
build(id << 1 | 1, mid + 1, r);
up(id);
}
void modify(int id, int l, int r, int ql, int qr, int val)
{
if (ql <= l && r <= qr)
{
settag(id, val);
return;
}
down(id);
int mid = (l + r) >> 1;
if (qr <= mid)
modify(id << 1, l, mid, ql, qr, val);
else if (ql > mid)
modify(id << 1 | 1, mid + 1, r, ql, qr, val);
else
{
modify(id << 1, l, mid, ql, qr, val);
modify(id << 1 | 1, mid + 1, r, ql, qr, val);
}
up(id);
}
info query(int id, int l, int r, int ql, int qr)
{
if (ql <= l && r <= qr)
{
return seg[id].val;
}
down(id);
int mid = (l + r) >> 1;
if (qr <= mid)
return query(id << 1, l, mid, ql, qr);
else if (ql > mid)
return query(id << 1 | 1, mid + 1, r, ql, qr);
else
return query(id << 1, l, mid, ql, qr) + query(id << 1 | 1, mid + 1, r, ql, qr);
}
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> p[i][0] >> p[i][1] >> p[i][2] >> p[i][3];
vec.push_back(p[i][1]);
vec.push_back(p[i][3]);
}
//对纵坐标y进行离散化
sort(all(vec));
vec.erase(unique(all(vec)), vec.end());
int m = vec.size() - 1;
build(1, 1, m);
for (int i = 1; i <= n; ++i)
{
int x1 = p[i][0];
int y1 = p[i][1];
int x2 = p[i][2];
int y2 = p[i][3];
y1 = lower_bound(all(vec), y1) - vec.begin() + 1;
y2 = lower_bound(all(vec), y2) - vec.begin();
eve.push_back({x1, 1, y1, y2});
eve.push_back({x2, -1, y1, y2});
}
//扫描线:以x轴升序扫描
sort(all(eve));
int prex = 0;
int len = seg[1].val.cnt; // 线段总长度
int ans = 0;
for (auto &it : eve)
{
int x = it[0];
int t = it[1];
int l = it[2];
int r = it[3];
int d = len;
if (seg[1].val.mi == 0) // 如果线段没有被全部覆盖
d -= seg[1].val.cnt;
ans += (x - prex) * d; // 先计算贡献
modify(1, 1, m, l, r, t); // 再进行区间修改
prex = x; //维护preX
}
cout << ans << endl;
}
例3·HH的项链

\(1 \leq n \leq 5\times 10^4\)
\(1 \leq a_i \leq 1e7\)
样例:
6
1 2 3 4 3 5
3
1 2
3 5
2 6
题解:莫队 / 扫描线 + 树状数组
- 看到数据范围后 ,发现显然可以用莫队求解,但是如果数据范围再大一点只能用扫描线来解决该问题了
- 我们将问题转化到二维平面上变成二维数点问题,更加直观,比如样例:
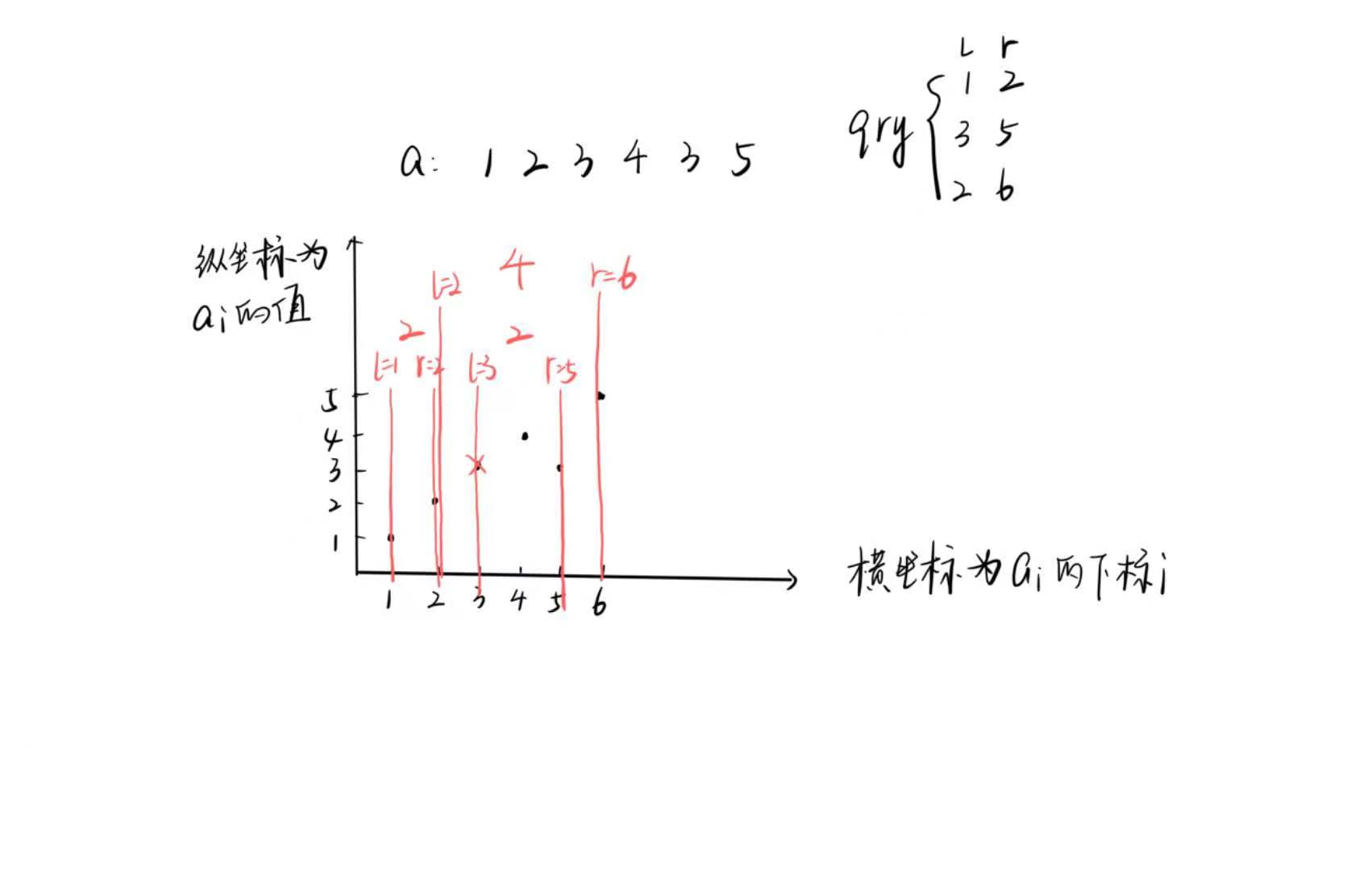
- 我们发现我们维护一个数的上一个出现的位置\(last\),如果某一个数的\(last\)存在,直接将\(last\)处的数删除即可,利用树状数组维护即可,这样的话始终能保证某个数只出现一次
- 所以我们按照询问的右端点升序扫描,每当扫描到一个查询的右端点,直接两个前缀和作差即可得到\([l,r]\)之间的点数
const int N = 1e6 + 10, M = 4e5 + 10;
int n, q;
int a[N];
int c[N];
vector<pii> qry[N];
int mp[N];
int ans[N];
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
while (x < N)
{
c[x] += val;
x += lowbit(x);
}
}
int get_sum(int x)
{
int res = 0;
while (x > 0)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int query(int l, int r)
{
return get_sum(r) - get_sum(l - 1);
}
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
cin >> q;
for (int i = 1; i <= q; ++i)
{
int l, r;
cin >> l >> r;
qry[r].push_back({l, i});
}
for (int i = 1; i <= n; ++i)
{
if (!mp[a[i]])
{
add(i, 1);
mp[a[i]] = i;
}
else
{
add(mp[a[i]], -1);
add(i, 1);
mp[a[i]] = i;
}
while (qry[i].size())
{
int l = qry[i].back().first;
int r = i;
ans[qry[i].back().second] = query(l, r);
qry[i].pop_back();
}
}
for (int i = 1; i <= q; ++i)
cout << ans[i] << endl;
}
二维偏序问题之逆序对
给定序列\(a\),请求出所有满足\(a_i > a_j \ \ \bigwedge\ \ i < j\)这个条件的对数
题解:扫描线 + 树状数组 + 离散化 / 归并排序
- 显然可以归并排序分治求逆序对
- 我们不妨考虑将其从一个二维偏序问题放到平面上转化为二维数点问题
- 显然我们对纵坐标进行离散化,树状数组维护纵坐标,然后从横坐标开始向右扫描,对于每一个点,设当前点的纵坐标为\(y\),我们只需要在树状数组中查询比纵坐标\(y\)大的点的个数即可
例4·The Union of k-Segments


题解:思维 + 扫描线
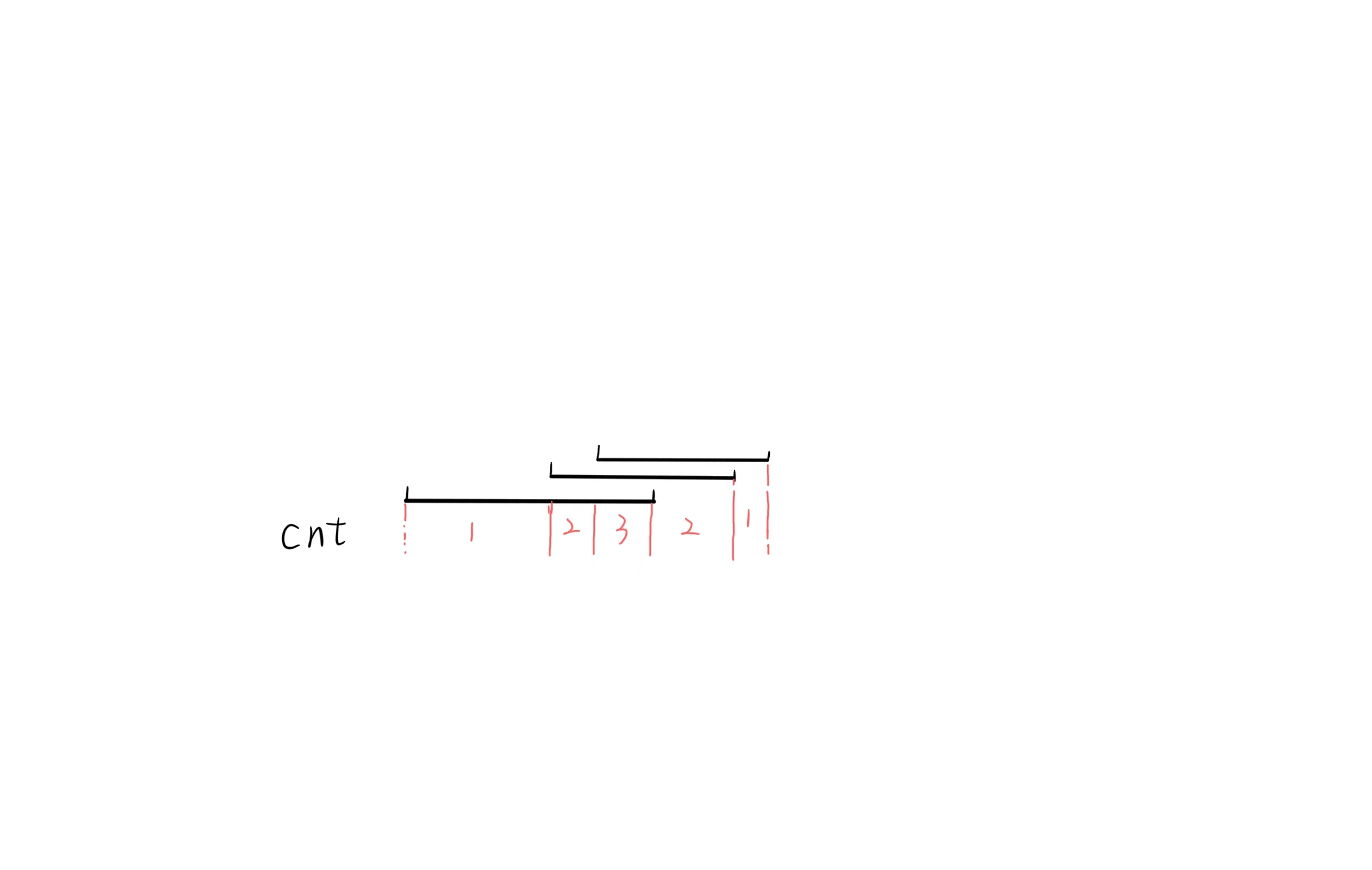
- 将线段按照左端点排序后从左往右进行扫描,维护\(cnt\):代表当前位置有\(cnt\)个线段重叠
- 当扫描到一个线段左端点,\(cnt:=cnt + 1\)
- 当扫描到一个线段右端点,\(cnt:=cnt - 1\)
- 当\(cnt=k\)时,说明是特殊区间的左端点,当\(cnt\)从\(k\)变成\(k-1\)时,说明是特殊区间的右端点
const int N = 2e6 + 10, M = 4e5 + 10;
int n, k;
vector<array<int, 2>> eve;
vector<pii> ans;
void solve()
{
cin >> n >> k;
for (int i = 1; i <= n; ++i)
{
int l, r;
cin >> l >> r;
eve.push_back({l, -1});
eve.push_back({r, 1});
}
sort(all(eve));
int cnt = 0;
bool flag = false;
pii tmp;
for (auto &it : eve)
{
int id = it[1];
if (id == -1)
cnt++;
else
cnt--;
if (cnt >= k && !flag)
{
tmp.first = it[0];
flag = true;
}
if (cnt < k && flag)
{
tmp.second = it[0];
flag = false;
ans.push_back(tmp);
}
}
cout << ans.size() << endl;
for (auto &it : ans)
cout << it.first << " " << it.second << endl;
}
例5·Goose, Goose, DUCK?
给定数组\(a\),求有多少个不同区间,这些区间中每个不同数出现的次数不为\(k\)次,求出这些不同的区间数
题解:线段树维护最小值和最小值数 + 扫描线思想
我们可以考虑初始为空数组,对于我们每次加入的数,我们将它看成右端点\(r\),我们要找出对于当前右端点\(r\)来说\([1,r-1]\)中存在多少个合法的左端点\(l\)(合法:区间\([l,r]\)中每个不同数出现的次数不为\(k\)次),我们在模拟时发现对于任意元素\(x\)在\([1,r]\)出现的位置\(p_1,p_2,p_3...p_m,m>=k\),那么对于这个数\(x\)而言不合法的区间为\([p_{m-k}+1,p_{m-k+1}]\),并且我们发现每次在添加一个新的数\(x\)进入数组后,如果原本\(x\)在\([1,r]\)出现的最后位置\(p_m且m>=k\),那么会撤销\(x\)之前的不合法区间,产生新的不合法区间
例如\(1,2,2,k=2\),现在对于2来说不合法区间为\([1,2]\),如果我们再添加一个2后,数组变为\(1,2,2,2,k=2\),那么现在\([1,2]\)变成了合法区间,产生了新的不合法区间\([3,3]\),所以我们可以把问题简化为撤销不合法区间看作区间\(-1\),产生新的合法区间看成区间\(+1\),然后答案即为\(0\)的数量
所以我们只需要使用线段树维护最小值和最小值的个数,然后如果区间的最小值为0,我们对答案就可以加上这段区间最小值0的个数;同时对于任意元素\(x\)出现的位置和个数我们可以利用邻接表的思想实现
const int N = 1e6 + 10, M = 4e5 + 10;
int n, k;
int a[N];
vector<int> v[N];
struct info
{
int cnt;
int minn;
};
struct node
{
int lazy, len;
info val;
} seg[N << 2];
info operator+(const info &a, const info &b)
{
info c;
c.minn = min(a.minn, b.minn);
c.cnt = 0;
if (c.minn == a.minn)
c.cnt += a.cnt;
if (c.minn == b.minn)
c.cnt += b.cnt;
return c;
}
void settag(int id, int tag)
{
seg[id].val.minn += tag;
seg[id].lazy += tag;
}
void up(int id)
{
seg[id].val = seg[id << 1].val + seg[id << 1 | 1].val;
}
void down(int id)
{
if (seg[id].lazy == 0)
return;
settag(id << 1, seg[id].lazy);
settag(id << 1 | 1, seg[id].lazy);
seg[id].lazy = 0;
}
void build(int id, int l, int r)
{
seg[id].len = r - l + 1;
if (l == r)
{
seg[id].val.minn = 0;
seg[id].val.cnt = 1;
seg[id].lazy = 0;
return;
}
int mid = (l + r) >> 1;
build(id << 1, l, mid);
build(id << 1 | 1, mid + 1, r);
up(id);
}
void modify(int id, int l, int r, int ql, int qr, int val)
{
if (ql <= l && r <= qr)
{
settag(id, val);
return;
}
down(id);
int mid = (l + r) >> 1;
if (qr <= mid)
modify(id << 1, l, mid, ql, qr, val);
else if (ql > mid)
modify(id << 1 | 1, mid + 1, r, ql, qr, val);
else
{
modify(id << 1, l, mid, ql, qr, val);
modify(id << 1 | 1, mid + 1, r, ql, qr, val);
}
up(id);
}
info query(int id, int l, int r, int ql, int qr)
{
if (ql <= l && r <= qr)
{
return seg[id].val;
}
down(id);
int mid = (l + r) >> 1;
if (qr <= mid)
return query(id << 1, l, mid, ql, qr);
else if (ql > mid)
return query(id << 1 | 1, mid + 1, r, ql, qr);
else
return query(id << 1, l, mid, ql, qr) + query(id << 1 | 1, mid + 1, r, ql, qr);
}
void solve()
{
cin >> n >> k;
for (int i = 1; i <= n; ++i)
cin >> a[i];
build(1, 1, n);
int ans = 0;
for (int i = 1; i <= n; ++i)
{
if (v[a[i]].size() >= k)
{
int l, r;
if (v[a[i]].size() == k)
l = 1, r = v[a[i]][v[a[i]].size() - k];
else
{
l = v[a[i]][v[a[i]].size() - k - 1] + 1;
r = v[a[i]][v[a[i]].size() - k];
}
// cout << l << ' ' << r << endl;
modify(1, 1, n, l, r, -1);
}
v[a[i]].push_back(i);
if (v[a[i]].size() >= k)
{
int l, r;
if (v[a[i]].size() == k)
l = 1, r = v[a[i]][v[a[i]].size() - k];
else
{
l = v[a[i]][v[a[i]].size() - k - 1] + 1;
r = v[a[i]][v[a[i]].size() - k];
}
modify(1, 1, n, l, r, 1);
}
if (query(1, 1, n, 1, i).minn == 0)
ans += query(1, 1, n, 1, i).cnt;
}
cout << ans << endl;
}
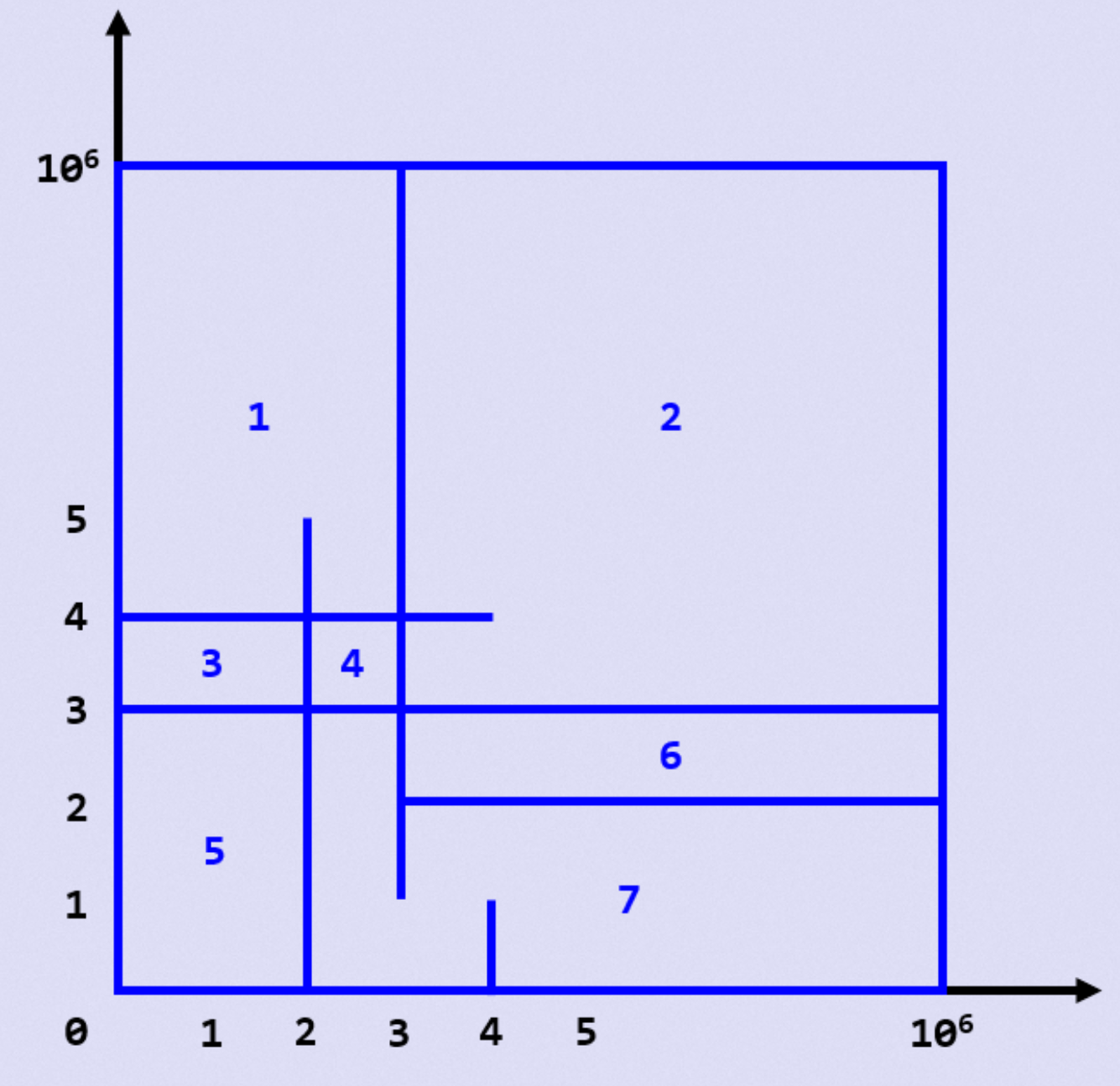
Divide Square
题解:扫描线 + 树状数组
- 手玩后发现分成的封闭的土地个数为线段交点数 + 1 + 分割整个土地的线段数量
- 所以我们只需要求出线段交点数即可
- 我们不妨利用利用树状数组维护纵坐标,遇到一条线段的左端点,就在相应的\(y\)值上 + 1,遇到一条线段的右端点- 1即可
- 我们以\(x\)轴从左往右进行扫描,如果遇到一条垂直的线,其纵坐标为\([l,r]\),查询区间和即可,区间和代表了在这个区间内横线的数量,即该垂直的直线和多少横线相交
- 注意先添加再查询,否则容易漏掉贡献
const int N = 1e6 + 10, M = 4e5 + 10;
int n, m;
int c[N];
vector<int> L[N];
vector<int> R[N];
map<int, pii> mp;
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
while (x < N)
{
c[x] += val;
x += lowbit(x);
}
}
int get_sum(int x)
{
int res = 0;
while (x > 0)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int query(int l, int r)
{
return get_sum(r) - get_sum(l - 1);
}
void solve()
{
cin >> n >> m;
int ans = 0;
for (int i = 1; i <= n; ++i)
{
int y, lx, rx;
cin >> y >> lx >> rx;
if (lx == 0 && rx == 1e6)
ans++;
L[lx].push_back(y);
R[rx].push_back(y);
}
for (int i = 1; i <= m; ++i)
{
int x, ly, ry;
cin >> x >> ly >> ry;
if (ly == 0 && ry == 1e6)
ans++;
mp[x] = mpk(ly, ry);
}
for (int i = 0; i <= 1e6; ++i)
{
while (L[i].size())
{
int y = L[i].back();
add(y, 1);
L[i].pop_back();
}
if (mp.count(i))
{
ans += query(mp[i].first, mp[i].second);
}
while (R[i].size())
{
int y = R[i].back();
add(y, -1);
R[i].pop_back();
}
}
cout << ans + 1 << endl;
}