暑期思维训练

LIS or Reverse LIS?

设一个长为 $n$ 的整数序列 $a$ 是 $\{a_1,a_2,a_3,\cdots,a_n\}$，那么 $a'$ 表示 $\{a_n,a_{n-1},a_{n-2},\cdots,a_1\}$，$\operatorname{LIS}(a)$ 表示 $a$ 的最长严格上升子序列的长度。

现在给定 $a$ 数组，请你将 $a$ 数组重新排列，使得重排后的 $\min(\operatorname{LIS}(a),\operatorname{LIS}(a'))$ 最大。

输入 $t$ 组数据，每组数据先输入 $n$ ，然后输入 $n$ 个整数，所有 $n$ 之和不超过 $2 \times 10^5$。

输出 $t$ 行，每行一组数据的答案，按输入顺序输出。

题解

容易发现当序列$a$被重排后形成单峰时答案一定最大

那么我们考虑如何将序列$a$以最优的形式重排成单峰

如果一个数$x$出现了两次，那么放在单峰的同一侧一定对答案没有贡献，所有我们可以$x$放在两侧，答案贡献 $+ 1$，如果$x$出现2次以上，因为是严格上升，所以不管我们把$x$多余的部分放在哪一侧，都不会产生新的贡献

如果说出现1次的数有$x$个，且$x$为奇数，我们可以将其中一个点作为单峰点，贡献为$\frac{x + 1}{2}$

如果说出现1次的数有$x$个，且$x$为偶数，那么没有单峰点，贡献为$\frac{x}{2}$

const int N = 2e5 + 10, M = 4e5 + 10;

int n;
int a[N];
map<int, int> mp;

void solve()
{
    cin >> n;
    mp.clear();
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        mp[a[i]]++;
    }
    int ans = 0;
    int sum = 0;
    for (auto [x, y] : mp)
    {
        if (y >= 2)
            ans++;
        else
            sum++;
    }
    cout << ans + (sum + 1) / 2 << endl;
}

Tokitsukaze and Strange Inequality

给一个长度为 $n$ 的排列，求有多少个四元组 $(a,b,c,d)$ 满足 $a<b<c<d$ 和 $p_a<p_c$、$p_b>p_d$。

$n\le 5000$

题解：前缀和dp / 树状数组

首先我们不妨枚举$b，c$，然后设$[1,b-1]$中$x$个数比$p_c$小，$[c + 1,n]$中有$y$个数比$p_b$小，那么对答案的贡献为$x \times y$，所以我们需要求出$x$和$y$

解法1：

我们不妨预处理$cnt[i][j]$，代表从第$i$个数到第$j$个数之间，有多少个数比$p_i$小

然后我们枚举$b,c$，并利用前缀和思想求出$x$和$y$即可

复杂度：$O(n ^ 2)$

解法2：

我们可以开两个树状数组预处理出$x,y$，复杂度$O(nlogn)$

然后我们枚举$b,c$，并利用前缀和思想求出$x$和$y$即可，复杂度$O(n ^ 2)$

const int N = 5e3 + 10, M = 4e5 + 10;

int n;
int a[N];
int c[N];
int Lcnt[N][N], Rcnt[N][N];

void solve()
{
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            Lcnt[i][j] = Rcnt[i][j] = 0;
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    for (int i = 1; i <= n; ++i)
    {
        int sum = 0;
        for (int j = i + 1; j <= n; ++j)
        {
            if (a[j] < a[i])
                sum++;
            Rcnt[i][j] = sum;
        }
    }
    for (int i = 1; i <= n; ++i)
    {
        int sum = 0;
        for (int j = i - 1; j >= 1; --j)
        {
            if (a[j] < a[i])
                sum++;
            Lcnt[i][j] = sum;
        }
    }
    ll ans = 0;
    for (int i = 1; i <= n; ++i) // 枚举b
    {
        for (int j = i + 1; j <= n; ++j) // 枚举c
        {
            ans += 1LL * (Rcnt[i][n] - Rcnt[i][j]) * (Lcnt[j][1] - Lcnt[j][i]);
        }
    }
    cout << ans << endl;
}

Infected Tree

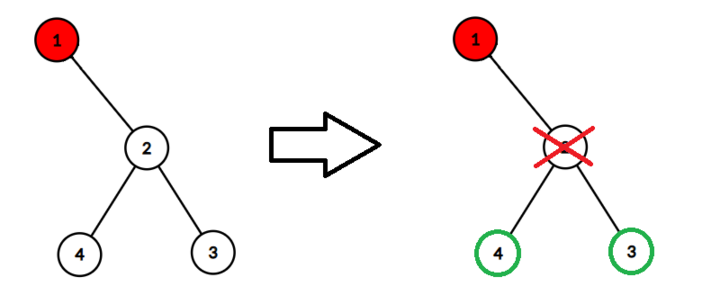
给定一棵以$1$ 号节点为根的二叉树，总节点个数为 $n$。

现在 $1$ 号节点感染了病毒，病毒每一回合都会去感染与该节点直接相连的节点，而你在这一回合里可以选择删除任意一个没有被病毒感染（尚未被删除）的点，这样就断开了它与其直接相连的点得关系.

询问最多可以有多少不被病毒感染的点，被删除的点不算做不被病毒感染的点

题解：树形$dp$ + 思维

容易发现病毒传染的路径一定是一条链，我们只要求出链长和被删除点的数量之和的最小值即可

一种情况病毒传染到叶子节点时结束，设节点的深度为$dep$，链长为$dep$，被删除的点数量为$dep - 1$

另一种情况病毒传染到只有一个儿子的节点结束，链长为$dep$，被删除的点的数量为$dep$

const int N = 3e5 + 10, M = 4e5 + 10;

int n;
vector<int> g[N];
int dep[N];
int mi = INF;

void dfs(int u, int par)
{
    dep[u] = dep[par] + 1;
    int cnt = 0;
    for (auto v : g[u])
    {
        if (v == par)
            continue;
        cnt++;
        dfs(v, u);
    }
    if (cnt == 0)
        mi = min(mi, 2 * dep[u] - 1);
    else if (cnt == 1)
        mi = min(mi, 2 * dep[u]);
}

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        dep[i] = 0;
        g[i].clear();
    }
    for (int i = 1, u, v; i <= n - 1; ++i)
    {
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    mi = INF;
    dfs(1, 0);
    cout << n - mi << endl;
}

AND Sequences

一个 $n$ 个数的非负数组如果 $\forall i\in\left[1,n\right)$ ，有 $a_1$ & $a_2$ & $……$ & $a_i = a_{i+1}$ & $a_{i+2}$ & $……$ & $a_n$ ，那么这个数组叫做 $“$ 好的数组 $”$ 。其中&表示按位与。

给定一个长度为 $n$ 的数组，求这个数组有多少种排列是 $“$ 好的数组 $”$ 。因为这个数字可能很大，所以输出结果模 $10^9+7$ 即可。

两个排列不同，指这个排列有一个位置的数与其他排列的这一位置的数的下表不同。

$ s_1 = s_2 : & : s_3 : & : s_4 : & : s_5 = 0 $ ,

$ s_1 : & : s_2 = s_3 : & : s_4 : & : s_5 = 0 $ ,

$ s_1 : & : s_2 : & : s_3 = s_4 : & : s_5 = 0 $ ,

$ s_1 : & : s_2 : & : s_3 : & : s_4 = s_5 = 0 $ .

题解

我们对于$a_1 = a_2 \&...\&a_m$和$a_1\&a_2...\&a_{m-1}=a_m$两边同时分别&上$a_1$和$a_m$

容易发现$a_1 = a_1\&a_2 \&...\&a_m=a_m$

那么只要我们找到这样的$a_1$和$a_m$，那么$a_1\&...\&a_i=a_{i+1}\&...\&a_m$一定成立

对于答案的贡献我们只要组合计数一下即可

const int N = 2e5 + 10, M = 4e5 + 10;

int n;
int a[N];
int fac[N];

void init()
{
    fac[0] = 1;
    for (int i = 1; i <= n; ++i)
        fac[i] = fac[i - 1] * i % mod;
}

void solve()
{
    cin >> n;
    init();
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    int sum = a[1];
    for (int i = 2; i <= n; ++i)
        sum &= a[i];
    int cnt = 0;
    for (int i = 1; i <= n; ++i)
    {
        if (a[i] == sum)
            cnt++;
    }
    cout << cnt * (cnt - 1) % mod * fac[n - 2] % mod << endl;
}

Plus and Multiply

有一个无穷大的正整数集合 $S$，该集合按下面所述方法生成：

数字 $1$ 在集合 $S$ 中。

若数字 $x$ 在该集合中，那么数 $x \times a$ 和数 $x+b$ 均在集合 $S$ 中。（其中 $a$ 与 $b$ 为给定常数）

现在给出数 $n,a,b$，请判断 $n$ 是否在集合 $S$ 中（此处给出的 $a$ 与 $b$ 就是上述集合生成方法中的 $a$ 和 $b$），若在请输出 Yes，否则输出 No。多组数据。

令数据组数为 $t$，那么有 $1 \leq t \leq 10^5$，$1 \leq n,a,b \leq 10^9$。

题解

对于集合中的一个数$x$

我们观察$x \times a + b $和$(x + b)\times a$

我们发现$(x + b) \times a = x \times a + a \times b$，也就是说对于先加$b$再乘$a$，我们可以转换为先乘$a$然后加上$a$个$b$

也就是这样我们可以一直进行乘法$\times a$操作，然后再进行$+b$操作

这样的话集合中数字一定可以表示成$a^x + y\times b$

那么我们只要枚举$x$即可判断$n$是否在集合中

时间复杂度为$O(log_a^n)$

注意当$a = 1$ 或者$b = 1$ 的时候需要特判

const int N = 2e5 + 10, M = 4e5 + 10;

void solve()
{
    int n, a, b;
    cin >> n >> a >> b;
    if (a == 1)
    {
        if (n % b == 1 || b == 1)
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
        return;
    }
    int sum = 1;
    while (sum <= n)
    {
        if ((n - sum) % b == 0)
        {
            cout << "Yes" << endl;
            return;
        }
        sum *= a;
    }
    cout << "No" << endl;
}

posted @ 2023-07-09 11:20 Zeoy_kkk 阅读(15) 评论(0) 编辑收藏举报

刷新页面返回顶部

Zeoy-kkk

暑期思维训练

LIS or Reverse LIS?

题解

Tokitsukaze and Strange Inequality

题解：前缀和dp / 树状数组

Infected Tree

Infected Tree

题解：树形\(dp\) + 思维

AND Sequences

题解

Plus and Multiply

题解

公告