Educational Codeforces Round 151 (Rated for Div
C. Strong Password
给定一个字符串\(s\),一个密码的长度\(m\),下界字符串\(l\)和上界字符串\(r\),上下界字符串长度均为\(m\),且字符只在0~9范围内,上界字符串的第 \(i\) 位非严格大于下界字符串的第 \(i\) 位,密码的第 \(i\) 位需要位于 \([l_i, r_i]\) 内。问是否存在一个密码不是\(s\)的子序列?
\(1 \leq m \leq 10\)
\(1 \leq |s| \leq 3\times 10^5\)
题解:贪心 + 枚举
- 因为\(m\)的范围比较小,所以我们不妨考虑枚举密码的每一位
- 根据题意得知,第\(i\)位密码\(ch\)必须保证在\([l_i,r_i]\)范围内
- 因为题目给出的是子序列,所以我们一旦选定了第\(i\)位密码为\(ch\),假设\(ch\)在\(s\)中存在且第一次出现的位置为\(pos\),那么第\(i+1\)位密码应该从\(s\)的第\(pos\)位之后开始搜索
- 我们不妨设\(s\)的第\(pos\)位之后的部分字符串为\(t\)
- 如果我们枚举到的密码在\(t\)中不存在,那么说明密码一定能被构造出来
- 如果第\(i\)位密码的所有情况在\(t\)中都存在的话,我们贪心地选择\([l_i,r_i]\)中第一次出现且在\(s\)中下标最大的字符作为第\(i\)位密码
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
void solve()
{
string s;
cin >> s;
int m;
cin >> m;
string l, r;
cin >> l >> r;
bool flag = false;
int p = 0;
for (int i = 0; i < m; ++i)
{
int mx = 0;
for (char j = l[i]; j <= r[i]; ++j)
{
int t = s.find(j, p);
if (t == -1)
{
flag = true;
break;
}
mx = max(mx, t);
}
p = mx + 1;
if (flag)
{
cout << "YES" << endl;
return;
}
}
cout << "NO" << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
cin >> T;
while (T--)
{
solve();
}
return 0;
}
D. Rating System
给定对局数\(n\),以及每个对局会使得\(rating\)的变化值\(a_i\),初始\(rating\)为\(0\)。问给定的低保线\(k\)(分数到\(k\)后无论\(rating\)怎么变不会低于\(k\))为多少时,\(n\)个对局后玩家的\(rating\)最高
题解:思维 + 最大后缀
- 容易发现答案应该是前缀和\(pre_i\)中的一个,但是如果我们枚举所有的前缀和复杂度显然为\(O(n^2)\),所以我们不妨逆向思维来考虑这个问题
- 设\(suf\_max_i\)为第\(i\)位之后的最大后缀,易得\(suf\_max[i] = max(suf[i+1],pre[n]-pre[i])\)
- 我们手模发现,对于任意一个\(k = pre_i\),最终的\(rating\)为\(pre_i + suf\_max_i\)
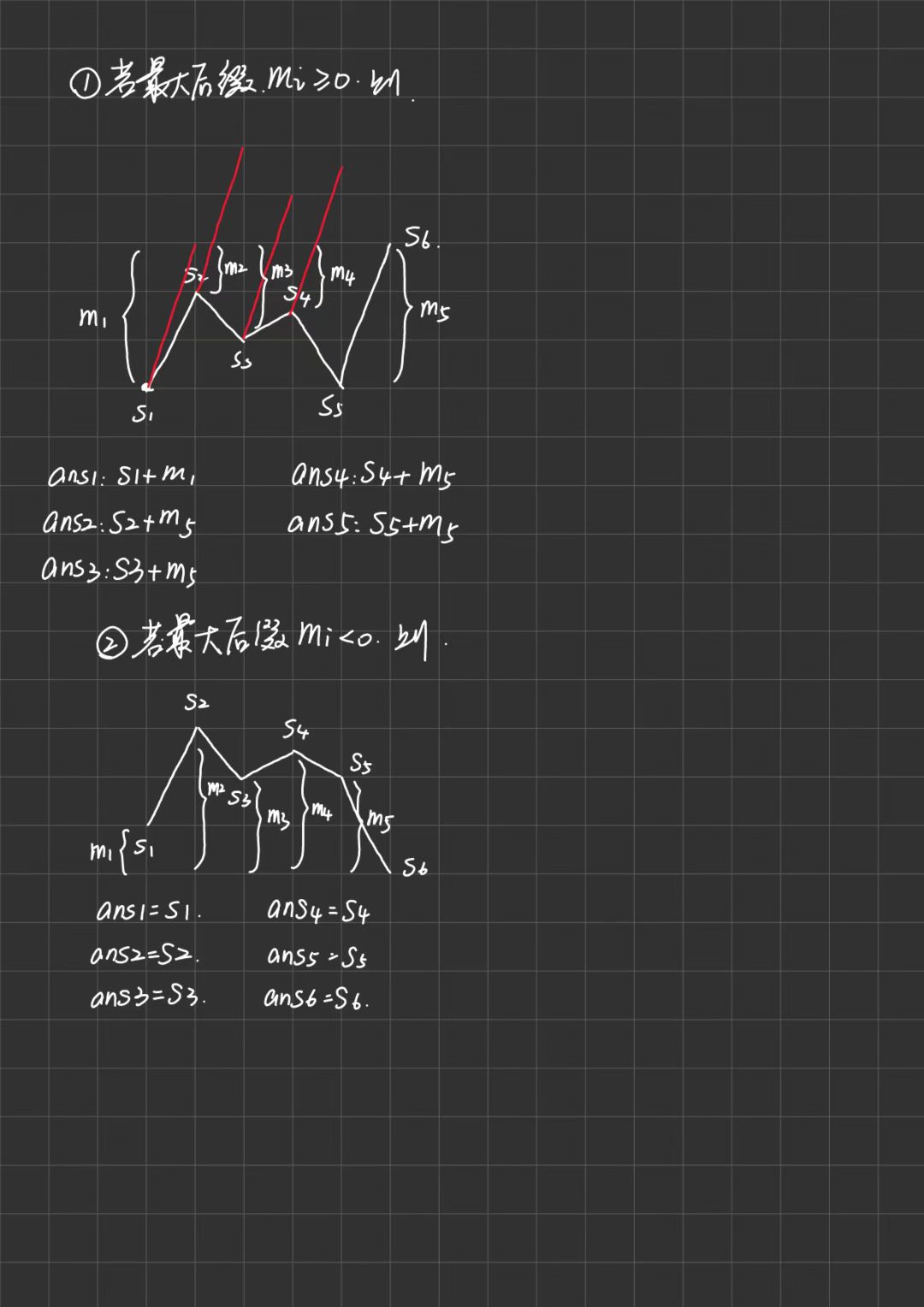
- 这样的话,时间复杂度为\(O(n)\)
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 3e5 + 10, M = 4e5 + 10;
int n;
int a[N];
int pre[N];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
for (int i = 1; i <= n; ++i)
pre[i] = pre[i - 1] + a[i];
vector<int> suf_max(n + 10);
for (int i = n; i >= 0; i--)
suf_max[i] = max(suf_max[i + 1], pre[n] - pre[i]);
int k = 0;
for (int i = 1; i <= n; ++i)
{
if (pre[k] + suf_max[k] < pre[i] + suf_max[i])
k = i;
}
cout << max(0LL, pre[k]) << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
cin >> T;
while (T--)
{
solve();
}
return 0;
}


