背包模型
背包模型
二维费用的背包问题
有 \(N\) 件物品和一个容量是 \(V\) 的背包,背包能承受的最大重量是 \(M\)。
每件物品只能用一次。体积是 \(v_i\),重量是 \(m_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。
输出最大价值。
题解:
状态表示:\(f[i][j][k]\):代表只从前\(i\)个物品中取,且背包容量不超过\(j\),背包重量不超过\(k\)所能获得的最大价值
状态属性:\(MAX\)
状态转移:
- 不选择第\(i\)个物品:\(f[i-1][j][k]\)
- 选择第\(i\)个物品:\(f[i-1][j-v_i][k-m_i]+w_i\)
\[f[i][j][k] = max(f[i-1][j][k],f[i-1][j-v_i][k-m_i]+w_i) \]状态优化:线性DP,滚动数组优化掉第一维即可
const int N = 1e3 + 10, M = 4e5 + 10;
int n, m1, m2;
int v1[N], v2[N], w[N];
int f[N][N];
void solve()
{
cin >> n >> m1 >> m2;
for (int i = 1; i <= n; ++i)
cin >> v1[i] >> v2[i] >> w[i];
for (int i = 1; i <= n; ++i)
for (int j = m1; j >= v1[i]; --j)
for (int k = m2; k >= v2[i]; --k)
f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + w[i]);
cout << f[m1][m2] << endl;
}
潜水员
潜水员为了潜水要使用特殊的装备。
他有一个带2种气体的气缸:一个为氧气,一个为氮气。
让潜水员下潜的深度需要各种数量的氧和氮。
潜水员有一定数量的气缸。
每个气缸都有重量和气体容量。
潜水员为了完成他的工作需要特定数量的氧和氮。
他完成工作所需气缸的总重的最低限度的是多少?
题解:二维费用的背包问题
状态表示:\(f[i][j][k]\):代表只从前i个气缸中选,使得选出的气缸氧气容量不少于\(j\)升,且氮气容量不少于\(k\)升的最小气缸重量
状态属性:\(MIN\)
状态计算:
不选第\(i\)个气缸:\(f[i-1][j][k]\)
选第\(i\)个气缸:\(f[i][max(0,j - v_{1i})][max(0,k-v_{2i})]\)
const int N = 1e3 + 10, M = 4e5 + 10;
int n, m, q;
int v1[N], v2[N], w[N];
int f[N][N];
void solve()
{
cin >> n >> m >> q;
for (int i = 1; i <= q; ++i)
cin >> v1[i] >> v2[i] >> w[i];
for (int i = 0; i <= n; ++i)
for (int j = 0; j <= m; ++j)
f[i][j] = INF;
f[0][0] = 0;
for (int i = 1; i <= q; ++i)
for (int j = n; j >= 0; --j)
for (int k = m; k >= 0; --k)
f[j][k] = min(f[j][k], f[max(j - v1[i], 0LL)][max(k - v2[i], 0LL)] + w[i]);
cout << f[n][m] << endl;
}
数字组合(硬币问题)
给定 \(N\) 个正整数 \(A_1,A_2,…,A_N\),从中选出若干个数,使它们的和为 \(M\),求有多少种选择方案。
题解:
状态表示:\(f[i][j]\):只从前\(i\)个数中选择数,使得这些选出的数之和为\(j\)的方案数
状态属性:数量
状态计算:
- 不选第i个数:\(f[i-1][j]\)
- 选第i个数: \(f[i-1][j-a[i]]\)
状态优化 : 滚动数组优化: \(f[j] += f[j - a[i]]\)
状态初始:\(f[0] = 1\)
const int N = 1e2 + 10, M = 1e4 + 10;
int n, m;
int a[N];
int f[M];
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
cin >> a[i];
f[0] = 1;
for (int i = 1; i <= n; ++i)
for (int j = m; j >= 1; --j)
if (j - a[i] >= 0)
f[j] += f[j - a[i]];
cout << f[m] << endl;
}
[NOIP2018 提高组] 货币系统
在网友的国度中共有 \(n\) 种不同面额的货币,第 \(i\) 种货币的面额为 \(a[i]\),你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 \(n\)、面额数组为 \(a[1..n]\) 的货币系统记作 \((n,a)\)。
在一个完善的货币系统中,每一个非负整数的金额 \(x\) 都应该可以被表示出,即对每一个非负整数 \(x\),都存在 \(n\) 个非负整数 \(t[i]\) 满足 \(a[i] \times t[i]\) 的和为 \(x\)。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 \(x\) 不能被该货币系统表示出。例如在货币系统 \(n=3\), \(a=[2,5,9]\) 中,金额 \(1,3\) 就无法被表示出来。
两个货币系统 \((n,a)\) 和 \((m,b)\) 是等价的,当且仅当对于任意非负整数 \(x\),它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 \((m,b)\),满足 \((m,b)\) 与原来的货币系统 \((n,a)\) 等价,且 \(m\) 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 \(m\)。
题解:完全背包解决极大线性无关组问题
- 容易发现我们需要找到一个最小的货币系统,且这个货币系统能够线性表示原来货币系统中所有的面值,所以实际上就是让我们求原来货币系统的极大线性无关组的大小
- 所以我们利用完全背包求出每种金额的货币的方案数,方案数为\(1\)的一定是极大线性无关组中的一员
- 即求出多少个货币的方案数为\(1\)即可
const int N = 2e5 + 10, M = 4e5 + 10;
int n;
int a[N];
int f[N];
void solve()
{
cin >> n;
int mx = -INF;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
mx = max(mx, a[i]);
}
for (int i = 0; i <= mx; ++i)
f[i] = 0;
f[0] = 1;
for (int i = 1; i <= n; ++i)
for (int j = a[i]; j <= mx; ++j)
f[j] += f[j - a[i]];
int ans = 0;
for (int i = 1; i <= n; ++i)
if (f[a[i]] == 1)
ans++;
cout << ans << endl;
}
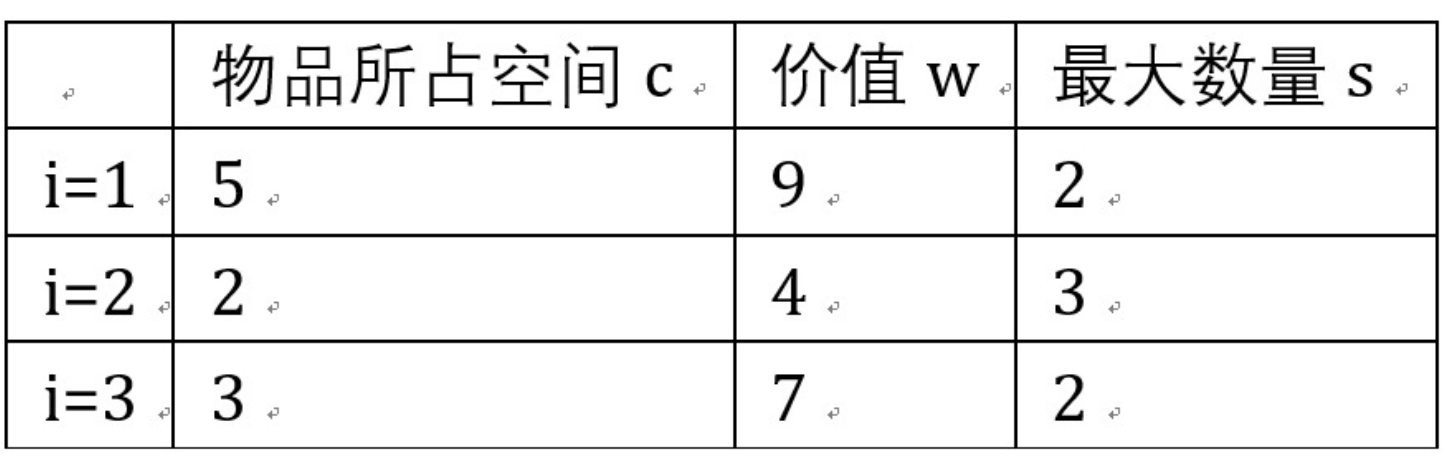
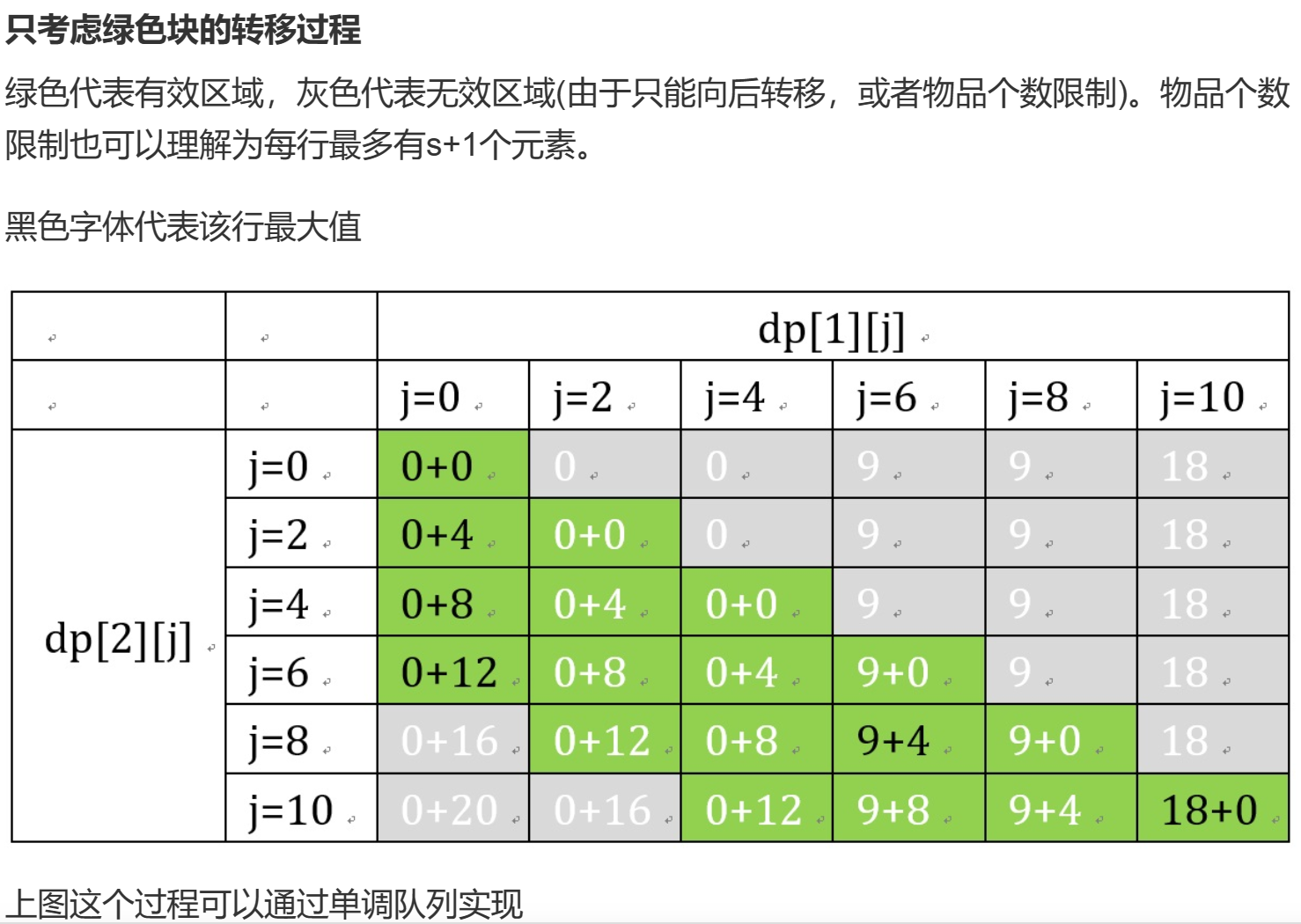
多重背包问题——单调队列优化
题解:\(O(n^2)\)
const int N = 1e3 + 10, M = 2e4 + 10;
int n, m;
int f[2][M];
int v[N], w[N], s[N];
int q[M], hh, tt;
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; ++i)
{
for (int r = 0; r < v[i]; ++r)
{
hh = 0, tt = -1;
for (int j = r; j <= m; j += v[i])
{
while (hh <= tt && j - s[i] * v[i] > q[hh])
hh++;
while (hh <= tt && f[i & 1 ^ 1][q[tt]] + (j - q[tt]) / v[i] * w[i] < f[i & 1 ^ 1][j])
tt--;
q[++tt] = j;
f[i & 1][j] = f[i & 1 ^ 1][q[hh]] + (j - q[hh]) / v[i] * w[i];
}
}
}
cout << f[n & 1][m] << endl;
}
混合背包问题
有 \(N\) 种物品和一个容量是 \(V\) 的背包。
物品一共有三类:
- 第一类物品只能用\(1\)次(01背包);
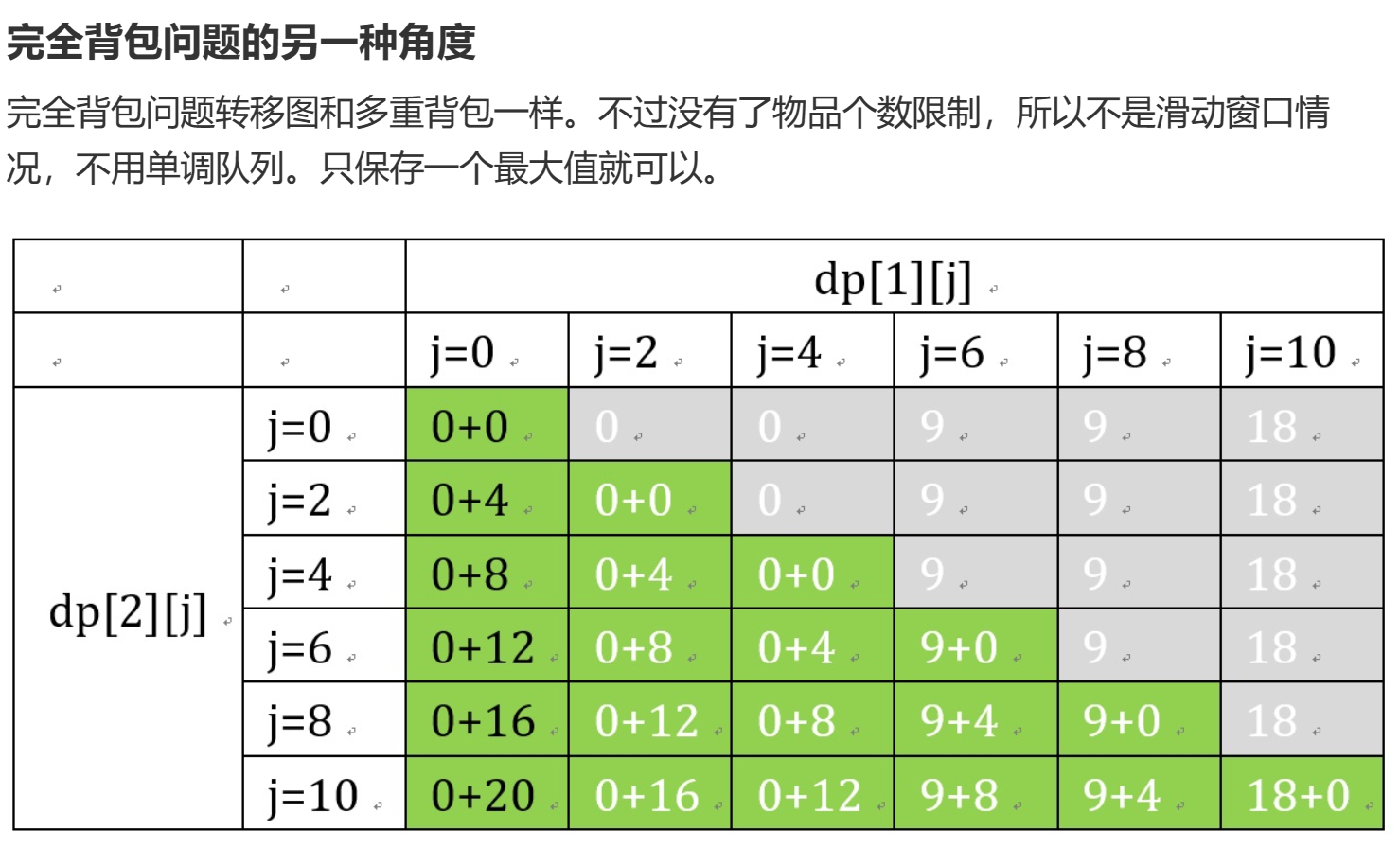
- 第二类物品可以用无限次(完全背包);
- 第三类物品最多只能用 \(s_i\) 次(多重背包);
每种体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
题解:
- 对于该类问题我们直接对每种背包问题逐个\(dp\)即可
- 我们不妨先利用二进制优化将多重背包变成01背包问题
- 然后完全背包就按完全背包的状态转移走,01背包就按01背包的状态转移走
const int N = 1e4 + 10, M = 4e5 + 10;
int n, m;
int f[N];
int v[N], w[N];
int idx;
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
int a, b, c;
cin >> a >> b >> c;
if (c == -1)
{
v[++idx] = a;
w[idx] = b;
}
else if (c > 0)
{
int k = 1;
while (k <= c)
{
v[++idx] = a * k;
w[idx] = b * k;
c -= k;
k <<= 1;
}
if (c)
{
v[++idx] = a * c;
w[idx] = b * c;
}
}
else
{
for (int j = a; j <= m; ++j)
f[j] = max(f[j], f[j - a] + b);
}
}
for (int i = 1; i <= idx; ++i)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
}
[NOIP2006 提高组] 金明的预算方案
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 \(n\) 元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
主件 附件 电脑 打印机,扫描仪 书柜 图书 书桌 台灯,文具 工作椅 无 如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 \(0\) 个、\(1\) 个或 \(2\) 个附件。每个附件对应一个主件,附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的 \(n\) 元。于是,他把每件物品规定了一个重要度,分为 \(5\) 等:用整数 \(1 \sim 5\) 表示,第 \(5\) 等最重要。他还从因特网上查到了每件物品的价格(都是 \(10\) 元的整数倍)。他希望在不超过 \(n\) 元的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 \(j\) 件物品的价格为 \(v_j\),重要度为\(w_j\),共选中了 \(k\) 件物品,编号依次为 \(j_1,j_2,\dots,j_k\),则所求的总和为:
\(v_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k}\)。
请你帮助金明设计一个满足要求的购物单。
题解:有依赖的背包问题——利用分组背包求解
- 因为每个主件的附件比较少,且附件没有附件,所以我们不妨将选择一个主件和其某些附件当成某组的一个方案,利用分组背包求解即可
- 状态表示:\(f[i][j]\)代表只在前\(i\)个组中选择决策,使得选出的物品的价格不超过\(j\)的最大价值
- 状态属性:\(MAX\)
- 状态转移:
显然我们不能按照分配给附件多少体积来划分,因为体积太大了,\(N*V*V\)显然会超时,但是我们发现每个主件最多只有2个附件,那么如果我们将每个主件及其附件看成一个物品组的话,最多只有4种情况,所以我们可以利用二进制枚举这四种组合,那么一个物品组中最多只会有4个物品,时间复杂度为\(O(4*N*V)\)
const int N = 60 + 10, M = 4e4 + 10;
int n, m;
int f[M];
int idx;
int V[N], W[N];
vector<pii> g[N];
void solve()
{
cin >> m >> n;
for (int i = 1; i <= n; ++i)
{
int a, b, c;
cin >> a >> b >> c;
if (c == 0)
V[i] = a, W[i] = b;
else
g[c].push_back({a, b});
}
for (int i = 1; i <= n; ++i) // 遍历物品组
{
if (!V[i]) // 如果不是主件直接continue,因为有了主件才有物品组
continue;
for (int j = m; j >= 0; j--) // 枚举体积
{
for (int k = 0; k < (1 << g[i].size()); ++k) // 枚举物品组中的物品(决策)
{
int v = V[i], w = V[i] * W[i]; // 主件必须选,因为依赖关系
for (int q = 0; q < g[i].size(); ++q) // 二进制枚举所有组合
{
if (k >> q & 1)
{
v += g[i][q].first;
w += g[i][q].first * g[i][q].second;
}
}
if (j - v >= 0)
f[j] = max(f[j], f[j - v] + w);
}
}
}
cout << f[m] << endl;
}
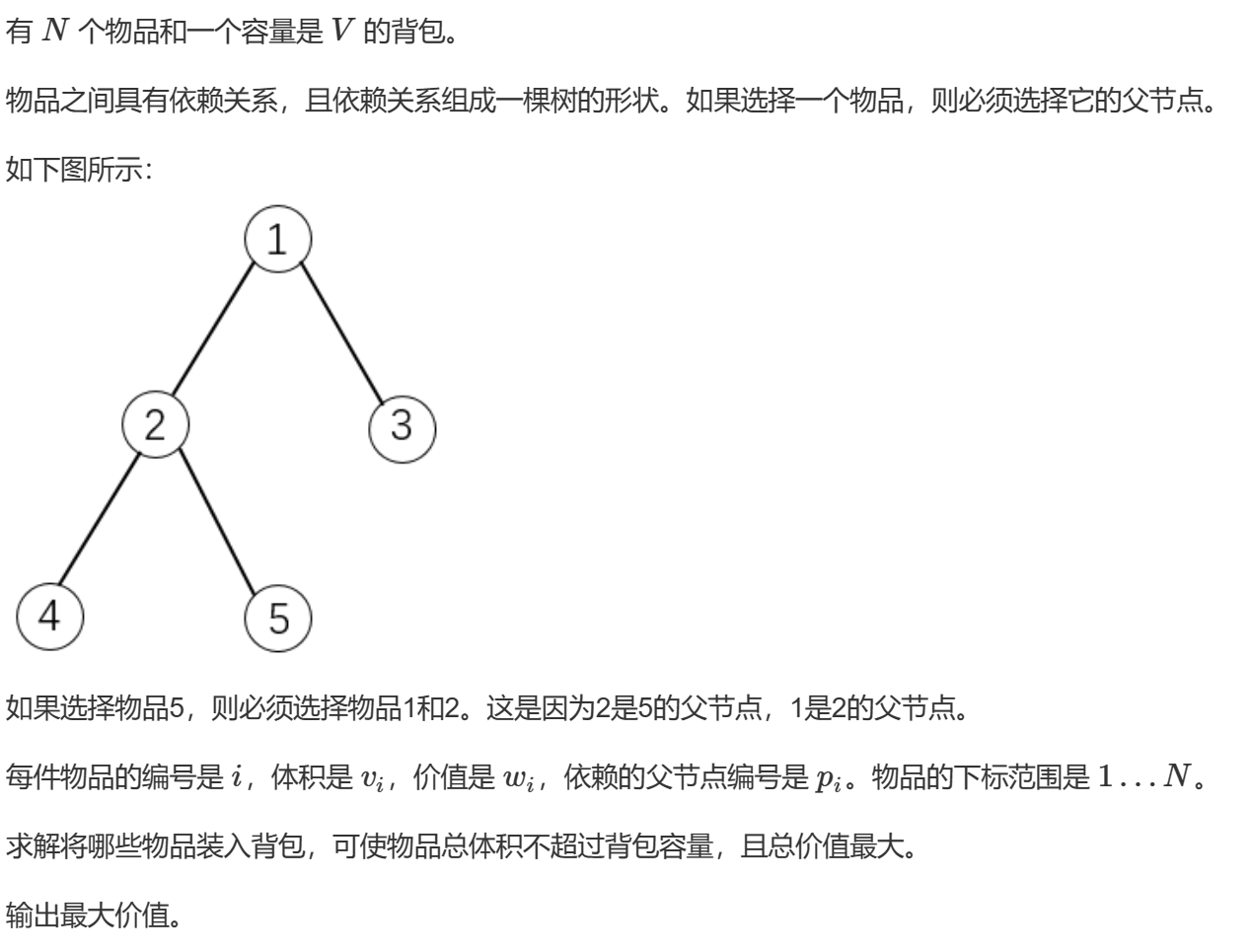
有依赖的背包问题
题解:树上背包 \(O(n\times v^2)\)
状态表示:\(f[u][i][j]\)代表只从以\(u\)为根的前\(i\)个子树中选,且选出的物品体积不超过\(j\)的最大价值
状态属性:\(MAX\)
状态计算:\(O(v ^ 2)\)
首先因为从\(u\)的子树中选,由于依赖关系,\(u\)必须选,所以剩余的可用体积为\(j-v[u]\),所以我们按照每个子树用了多少体积来划分;
我们可以将每个子树\(v\)看成一个物品组,每一个物品(决策)就是分配\(k\)个体积给该子树,那么每个物品的体积为\(k\),价值为\(f[v][v_{son}][k],v_{son}\)是节点\(v\)的子节点个数\[f[u][i][j] = max(f[u][i][j],f[u][i-1][j-k] + f[v][v_{son}][k]) \]
状态优化:我们发现状态只和上一层状态有关,我们优化掉第二维,倒序遍历体积
\(f[u][j] = max(f[u][j],f[u][j-k] + f[v][k])\)状态初始:
\(f[u][j] = f[u][j - v[u]] + w[u]; j > v[u]\)
\(f[u][j] = 0,j < v[u]\)
const int N = 1e2 + 10, M = 4e5 + 10;
int n, m;
int f[N][N];
int v[N], w[N];
vector<int> g[N];
void dfs(int u, int par)
{
for (auto V : g[u]) // 遍历物品组,即遍历子节点
{
if (V == par)
continue;
dfs(V, u);
for (int j = m - v[u]; j >= 0; j--) // 遍历预留好u后的体积
for (int k = 0; k <= j; ++k) // 遍历决策
f[u][j] = max(f[u][j], f[u][j - k] + f[V][k]);
}
for (int j = m; j >= v[u]; j--) // 将预留好的u放入
f[u][j] = f[u][j - v[u]] + w[u];
for (int j = 0; j < v[u]; ++j) // 清空无法选u的所有状态
f[u][j] = 0;
}
void solve()
{
int rt = 1;
cin >> n >> m;
for (int i = 1, u; i <= n; ++i)
{
cin >> v[i] >> w[i] >> u;
if (u == -1)
{
rt = i;
continue;
}
g[u].push_back(i);
g[i].push_back(u);
}
dfs(rt, -1);
cout << f[rt][m] << endl;
}
背包问题求最优解方案数
题解:
- 我们不妨在状态转移的时候进行计数\(dp\)
- 状态表示:\(g[i][j]\)代表只从前\(i\)个物品中选,且选出的物品的总体积恰好为\(j\)的最大价值的方案数
- 状态属性:数量
- 状态转移:
- \(f[i-1][j] > f[i-1][j-v_i]+w_i\),\(g[i][j] += g[i-1][j]\)
- \(f[i-1][j] < f[i-1][j-v_i]+w_i\),\(g[i][j] += g[i-1][j-v_i]\)
- \(f[i-1][j] = f[i-1][j-v_i]+w_i\),\(g[i][j] += g[i-1][j-v_i] + g[i-1][j]\)
- 状态初始:\(g[0][0] =1\)
- 答案呈现:\(\sum g[n][i]\ \ 且 \ \ f[n][i] = f[n][m]\)
const int N = 1e3 + 10, M = 4e5 + 10;
int n, m;
int f[N][N];
int g[N][N];
int v[N], w[N];
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
cin >> v[i] >> w[i];
g[0][0] = 1;
for (int i = 1; i <= n; ++i)
{
for (int j = 0; j <= m; ++j)
{
if (j - v[i] < 0)
{
f[i][j] = f[i - 1][j];
g[i][j] = (g[i][j] + g[i - 1][j]) % mod;
}
else
{
if (f[i - 1][j] > f[i - 1][j - v[i]] + w[i])
{
f[i][j] = f[i - 1][j];
g[i][j] = (g[i][j] + g[i - 1][j]) % mod;
}
else if (f[i - 1][j] < f[i - 1][j - v[i]] + w[i])
{
f[i][j] = f[i - 1][j - v[i]] + w[i];
g[i][j] = (g[i][j] + g[i - 1][j - v[i]]) % mod;
}
else
{
f[i][j] = f[i - 1][j];
g[i][j] = (g[i][j] + g[i - 1][j] + g[i - 1][j - v[i]]) % mod;
}
}
}
}
int ans = 0;
for (int i = 0; i <= m; ++i)
{
if (f[n][i] == f[n][m])
ans = (ans + g[n][i]) % mod;
}
cout << ans << endl;
}
背包问题求字典序最小的具体方案
题解:
- 我们求字典序最小的方案需要从前往后递推,但是一般我们\(dp\)输出方案的时候都是从后往前根据转移找的
- 所以在本题我们需要先从后往前\(dp\),也就是说我们倒序遍历物品的顺序,这样的话我们就可以从第一个物品开始正序求字典序最小的方案
- 观察倒序遍历物品后的01背包的状态转移方程:
\(f[i][j] = max(f[i+1][j],f[i+1][j-v[i]] + w[i])\)- 我们贪心的思考,如果我们能选第\(i\)个物品,那我们一定要选,因为这样字典序一定是最小的
如果我们不能选第\(i\)个物品 ,那么我们就不选
const int N = 1e3 + 10, M = 4e5 + 10;
int n, m;
int f[N][N];
int v[N], w[N];
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
cin >> v[i] >> w[i];
for (int i = n; i >= 1; --i)
for (int j = 0; j <= m; ++j)
if (j - v[i] < 0)
f[i][j] = f[i + 1][j];
else
f[i][j] = max(f[i + 1][j], f[i + 1][j - v[i]] + w[i]);
vector<int> ans;
int pre = f[1][m];
int j = m;
for (int i = 1; i <= n; ++i)
{
if (j - v[i] >= 0 && pre == f[i + 1][j - v[i]] + w[i])
{
pre = f[i + 1][j - v[i]];
j = j - v[i];
ans.push_back(i);
}
else
pre = f[i + 1][j];
}
for (auto it : ans)
cout << it << " ";
cout << endl;
}