2023-05 多校联合训练 HZNU站
我想要原石
然而,由于提瓦特大陆实在是太大了,游戏中设置了许多传送锚点。众所周知,每个传送锚点附近都有若干个原石(其实并没有),曾经有一位丰富经验的旅行者开辟了 \(n−1\) 条路和 \(n\) 个由路连通的传送锚点。为了便于后续的旅行者知道地图上原石的分布情况,他决定给旅行者一些提示,但是他没有直接将每个传送锚点附近的原石标注,而是标注了他所走过的路径的权值来考验后续的旅行者。对于一条路径连接的两个点 \(u,v\) 其权值为:点 \(u\) 的原石数量异或点 \(v\) 的原石数量。
现在你来到了这片提瓦特大陆,但是你现在只有一次传送机会——即你可以选择一个传送锚点并到达,并且你将知道这个点的原石数量,请聪明的你回答这 \(n\) 个传送锚点附近原石数量的异或和。
你需要回答 \(q\) 次询问,每次询问告诉你传送的点及该点所有的原石数量,请你根据已有信息推断出这 \(n\) 个传送锚点附近原石数量的异或和。
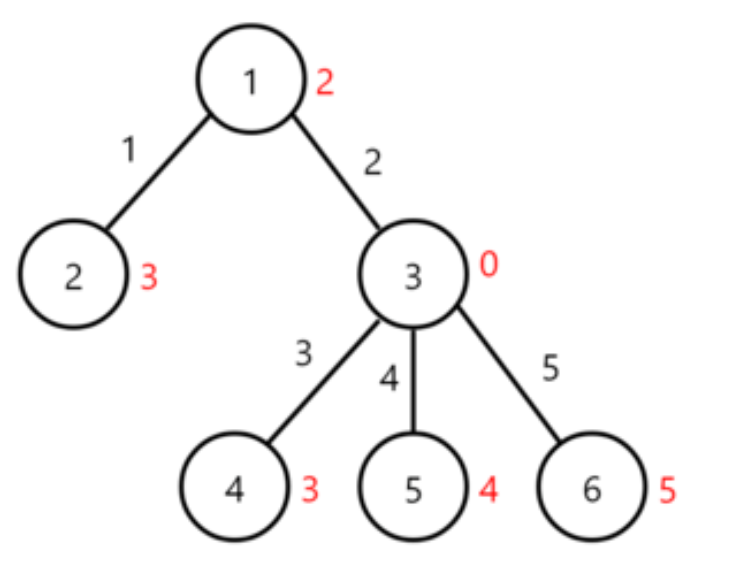
题解:换根\(DP\)
- 容易发现,当我们知道\(u\)的值后,那么\(v\)的值就是\(u\)的值异或上\(u\)到\(v\)路径上所有边权
- 那么容易发现,如果一条边对答案的贡献为:下边的节点的子树大小
- 所以我们可以先以任意一个点为根,\(dfs\)求出所有点的子树大小,并树形\(dp\)求出根节点的答案值
- 然后我们在通过\(dfs\)换根\(dp\)自上而下求出所有点的答案
- 那么在询问的时候,如果\(n\)为偶数,答案还要异或上\(x\),否则直接输出,\(O(1)\)
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
int n, q;
vector<pii> g[N];
int ans[N];
int sz[N];
int res;
void dfs(int u, int par)
{
sz[u] = 1;
for (auto [v, w] : g[u])
{
if (v == par)
continue;
dfs(v, u);
sz[u] += sz[v];
if (sz[v] % 2 == 1)
res ^= w;
}
}
void DFS(int u, int par)
{
for (auto [v, w] : g[u])
{
if (v == par)
continue;
if ((sz[u] - sz[v] + n - sz[u]) % 2 == 1 && sz[v] % 2 == 0)
ans[v] = ans[u] ^ w;
else if ((sz[u] - sz[v] + n - sz[u]) % 2 == 0 && sz[v] % 2 == 1)
ans[v] = ans[u] ^ w;
DFS(v, u);
}
}
void solve()
{
cin >> n;
for (int i = 1; i < n; ++i)
{
int u, v, w;
cin >> u >> v >> w;
g[u].push_back({v, w});
g[v].push_back({u, w});
}
dfs(1, 0);
for (int i = 1; i <= n; ++i)
ans[i] = res;
DFS(1, 0);
cin >> q;
while (q--)
{
int u, x;
cin >> u >> x;
if (n % 2)
cout << (ans[u] ^ x) << endl;
else
cout << ans[u] << endl;
}
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}


