HEUCPC2021

stral Reflection

在 \([1,n]\)上支持如下操作：

操作一：学习一个新的技能——清除 \([l,r]\)内所有的陨石

操作二：给定一个点集\(k\)代表陨石出现在这些位置，询问最少需要使用多少技能才能清除所有陨石（不能使用当前没有学习的技能）

共操作\(m\)次

\(\sum k \leq 1e5\)

\(m \leq 1e5\)

\(n \leq 1e5\)

题解：线段树 + 贪心

容易看出一定是在线查询

不管怎么样，最左边的陨石一定会被清除

所以我们不妨从最左边开始清除尽量多的陨石，也就是说，我们需要找到\(l\)比当前陨石小的，且右端点\(r\)最大的区间，贪心的消除尽量多的陨石

那么我们可以利用线段树维护区间最大值，支持单点修改和区间查询即可，每次执行操作一就在\(l\)处加上\(r\)即可，假设当前需要清除陨石的位置为\(p\)，查询时直接查询\([1,p]\)中的最大值即可，最大值即为最远的右端点

时间复杂度：\(O(m + \sum k) logn\)

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e5 + 10, M = 4e5 + 10;

int n, m;
struct info
{
    int maxx;
};

struct node
{
    info val;
} seg[N << 2];

info operator+(const info &a, const info &b)
{
    info c;
    c.maxx = max(a.maxx, b.maxx);
    return c;
}

void up(int id)
{
    seg[id].val = seg[lson].val + seg[rson].val;
}

void change(int id, int l, int r, int x, int val)
{
    if (l == r)
    {
        seg[id].val.maxx = max(seg[id].val.maxx, val);
        return;
    }
    int mid = l + r >> 1;
    if (x <= mid)
        change(lson, l, mid, x, val);
    else
        change(rson, mid + 1, r, x, val);
    up(id);
}

info query(int id, int l, int r, int ql, int qr)
{
    if (ql <= l && r <= qr)
        return seg[id].val;
    int mid = l + r >> 1;
    if (qr <= mid)
        return query(lson, l, mid, ql, qr);
    else if (ql > mid)
        return query(rson, mid + 1, r, ql, qr);
    else
        return query(lson, l, mid, ql, qr) + query(rson, mid + 1, r, ql, qr);
}

void solve()
{
    cin >> n >> m;
    while (m--)
    {
        int op, l, r, w, k;
        cin >> op;
        if (op == 1)
        {
            cin >> l >> r >> w;
            change(1, 1, n, l, r);
        }
        else
        {
            cin >> k;
            queue<int> q;
            for (int i = 1; i <= k; ++i)
            {
                int x;
                cin >> x;
                q.push(x);
            }
            int ans = 0;
            bool flag = true;
            while (q.size())
            {
                int max_R = query(1, 1, n, 1, q.front()).maxx;
                if (max_R < q.front())
                {
                    flag = false;
                    break;
                }
                ans++;
                while (q.size() && q.front() <= max_R)
                    q.pop();
            }
            if (flag)
                cout << ans << endl;
            else
                cout << -1 << endl;
        }
    }
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

hivalric Blossom

有 \(n\) 个任务，你需要给每个任务指定一个优先级，之后你会按优先级递增的顺序完成这些任务。如果有两个任务优先级相同，你会先完成编号小的。现在有 \(m\) 对任务必须连续完成，你的目标是在满足这些限制的情况下，让不同优先级的数量尽可能少。

题解：思维

容易发现根据题目的限制产生了许多链，我们的任务就是给这些链染色，即指定优先级

首先同一条链上的点的颜色一定相同，被一条链框住的这些节点的颜色一定和该链颜色不同

所以我们不妨维护一个初始拥有\(n\)种颜色的集合，提前预处理好每个点的前驱和后继

如果该点是一条链的头节点，我们就从颜色集合中取出一个颜色，分配给链头，然后在集合中将该颜色删除

如果该点既不是链头也不是链尾，那就染上和链头一样的颜色，因为记录了该点的前驱，所以染的颜色取前驱的颜色即可

如果该点是一条链的链尾，染上前驱的颜色后将该颜色添加会颜色集合中

时间复杂度：\(O(nlogn)\)

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e5 + 10, M = 4e5 + 10;

int n, m;
int L[N], R[N];
set<int> st;
int ans[N];

void solve()
{
    cin >> n >> m;
    for (int i = 1; i <= m; ++i)
    {
        int a, b;
        cin >> a >> b;
        L[b] = a;
        R[a] = b;
    }
    for (int i = 1; i <= n; ++i)
        st.insert(i);
    for (int i = 1; i <= n; ++i)
    {
        if (!L[i])
        {
            ans[i] = *st.begin();
            if (R[i])
                st.erase(st.lower_bound(*st.begin()));
        }
        else
        {
            ans[i] = ans[L[i]];
            if (!R[i])
                st.insert(ans[i]);
        }
    }
    for (int i = 1; i <= n; ++i)
        cout << ans[i] << "\n "[i < n];
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

clipsing Star

\(n\) 轮游戏，每轮有 \(a_i\) 块钱。在一轮中，先手可以自己拿 \(b_i\) 块钱，给后手 \(a_i−b_i\) 块钱，然后交换先后手的概率为 \(\frac{b_i}{a_i}\)，问最优策略下先手方与后手方总钱数之差的最大值。

题解：思维

我们考虑最后\(n-1\)轮和第\(n\)轮的情况，想要钱数之差最大，先手要么不取\(a_{n-1}\)，要么取

所以在不考虑前面轮数的情况下，最后两轮钱数之差的最大值一定为\(| a_n-a_{n-1}|\)

容易发现我们可以把最后两轮归结为钱数为\(| a_n-a_{n-1}|\)的一轮

那么我们从后往前一直归结，只剩最后一轮的时候就是答案

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e6 + 10, M = 4e5 + 10;

int n;
int a[N];

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    for (int i = n; i >= 2; i--)
        a[i - 1] = abs(a[i] - a[i - 1]);
    cout << a[1] << endl;
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

andelion Knight

给定 \(01\) 序列 \(a,b\)，对于 \(x∈[0,2n]\)，询问有多少方案可以在 \(a\) 和 \(b\) 各选择一个前缀，使得两个前缀的长度之和为 \(x\) 且两个前缀的和相等。我们定义上面的方案数为\(f(x)\)，请你求出所有的\(f(x),x∈[0,2n]\)

思维 + 差分

我们不妨先预处理出序列\(b\)中所有前缀中每个数\(i\)的起始位置\(l_i\)和结束位置\(r_i\)

然后遍历序列\(a\)，求其前缀和\(pre_j\)，如果序列\(b\)中存在相同的前缀和\(i\)，那么\(f(l_i + j,r_i+j)\)之间的答案都要加上\(1\)

对于区间加的操作可以使用差分数组/树状数组维护差分/线段树实现

如果使用差分数组实现，时间复杂度为\(O(n)\)

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e6 + 10, M = 4e5 + 10;

int n;
int ans[N << 1];
int a[N], b[N];
int L[N], R[N];
int pre[N];

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        L[i] = INF, R[i] = -INF;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    for (int i = 1; i <= n; ++i)
        cin >> b[i];
    for (int i = 1; i <= n; ++i)
    {
        pre[i] = pre[i - 1] + b[i];
        L[pre[i]] = min(L[pre[i]], i);
        R[pre[i]] = max(R[pre[i]], i);
    }
    int sum = 0;
    if (L[sum] != INF)
    {
        ans[L[sum]]++;
        ans[R[sum] + 1]--;
    }
    for (int i = 1; i <= n; ++i)
    {
        sum += a[i];
        if (L[sum] != INF)
        {
            ans[L[sum] + i]++;
            ans[R[sum] + i + 1]--;
        }
    }
    for (int i = 1; i <= 2 * n; ++i)
        ans[i] = ans[i - 1] + ans[i];
    for (int i = 0; i <= 2 * n; ++i)
        cout << ans[i] << "\n "[i < 2 * n];
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

uvenile Galant

询问将两种给定形状拼接成一个指定长度的直角梯形的方案数。

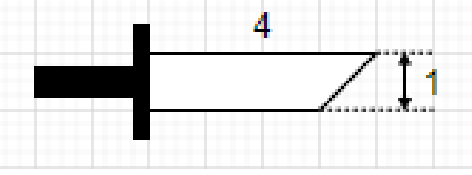
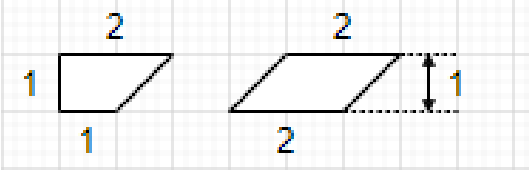
题解：\(DP\) + 简单状态机模型

容易发现是简单\(dp\)，并且是状态机模型

状态表示：
\(f[i][0/1/2]\)代表较短的边长度为\(i\)的时，\(0\)代表\(i\)右端是平的，\(1\)代表\(i\)右端尖角朝下，\(2\)代表\(i\)右端尖角朝上的方案数
状态属性：数量
状态转移：状态机模型如下

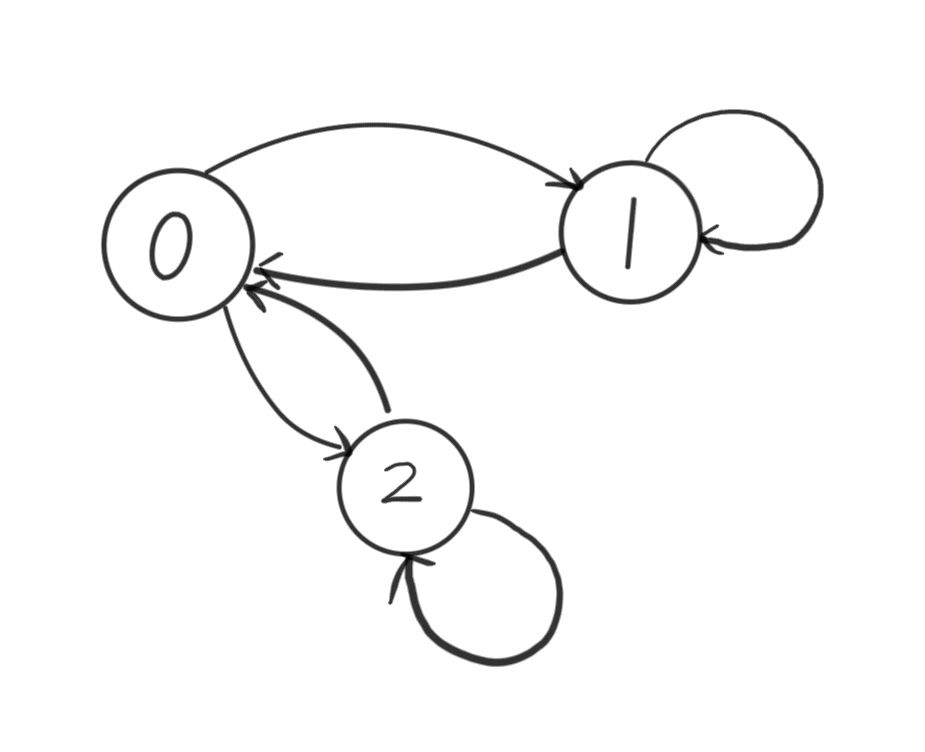
状态转移方程不再赘述
状态机入口：\(1 / 2\)
状态初始：\(f[0][0] = 1,f[1][1] = 1,f[1][2] = 1\)
状态机出口：\(2\)
答案呈现：\(f[n-1][2]\)

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const double eps = 1e-9;
const int N = 1e6 + 10, M = 4e5 + 10;

int n;
int f[N][3];

void solve()
{
    cin >> n;
    f[0][0] = 1;
    f[1][1] = 1;
    f[1][2] = 1;
    for (int i = 1; i <= n; ++i)
    {
        f[i][0] = (f[i - 2][1] % mod + f[i - 2][2] % mod) % mod;
        f[i][1] = (f[i - 2][1] % mod + f[i - 1][0] % mod) % mod;
        f[i][2] = (f[i - 1][0] % mod + f[i - 2][2] % mod) % mod;
    }
    cout << f[n - 1][2] << endl;
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

posted @ 2023-05-24 14:22 Zeoy_kkk 阅读(8) 评论(0) 编辑收藏举报

刷新页面返回顶部

Zeoy-kkk

HEUCPC2021

stral Reflection

题解：线段树 + 贪心

hivalric Blossom

题解：思维

clipsing Star

题解：思维

andelion Knight

思维 + 差分

uvenile Galant

题解：\(DP\) + 简单状态机模型

公告