状态机模型
状态机代表一系列有序的事件,我们通过状态机能够将一个复杂的状态拓展为几个简单过程
状态机是一种另类的状态表示方式,实际上是我们将每一个状态拓展成一个过程
任何一个方案都能唯一对应一个状态机
简单的说,我们可以通过状态机将一个复杂、混沌的状态细分成几个清晰的状态
状态机在任意时刻的状态大多为
0或1状态机需要考虑入口和出口
大盗阿福
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有
家店铺,每家店中都有一些现金。 阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
题解:线性DP——状态机模型
第一种非线性
: 状态表示:
代表只从前 个店铺中偷窃,能够获得的最大价值 状态属性:
状态计算:
- 选择不偷窃第
个店铺: - 选择偷窃第
个店铺,那我们一定无法偷窃第 个店铺:
状态初始:
答案呈现:
第二种线性
(状态机模型): 状态表示:
代表只从前 个店铺中选,且 代表选择第 家店铺, 代表不选第 家店铺所能获得的最大价值
状态属性:
状态计算:按照路径来划分集合,若选择某店铺,将其状态表示为
,若不选某个店铺,将其状态表示为 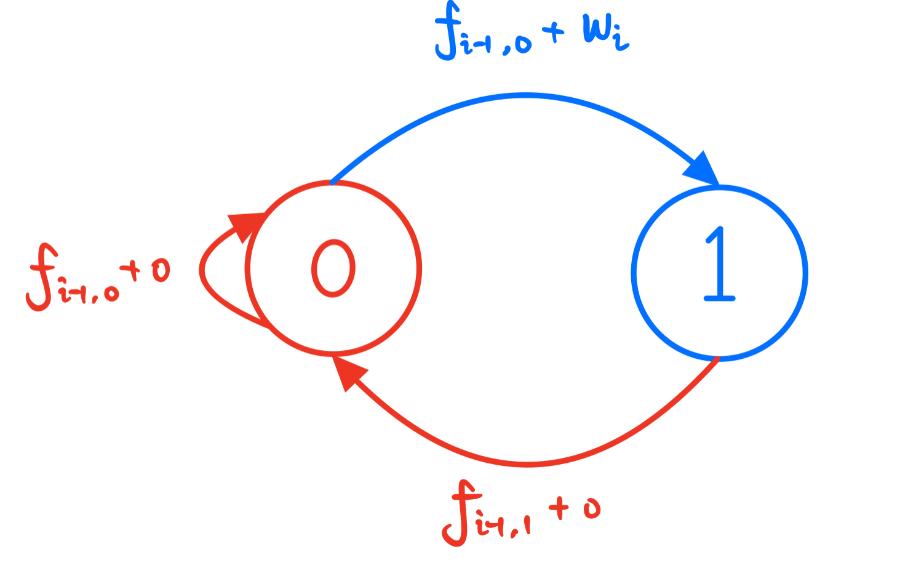
- 选择第
个店铺,那么我们肯定不选择第 家店铺,即只有一条边从状态 通向状态 ,即 - 不选择第
个店铺,那么第 家店铺可以选择也可以不选择,即有两条路径可以从其他状态到状态 ,即
状态初始:
状态机入口:
,状态机出口: 或 答案呈现:
//第一种dp
const int N = 2e5 + 10, M = 4e5 + 10;
int n;
int f[N];
int w[N];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> w[i];
for (int i = 0; i <= n; ++i)
f[i] = 0;
f[0] = 0;
f[1] = w[1];
for (int i = 2; i <= n; ++i)
f[i] = max(f[i - 1], f[i - 2] + w[i]);
cout << f[n] << endl;
}
//第二种dp
const int N = 2e5 + 10, M = 4e5 + 10;
int n;
int w[N];
int f[N][2];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> w[i], f[i][1] = f[i][0] = 0;
for (int i = 1; i <= n; ++i)
{
f[i][1] = max(f[i][1], f[i - 1][0] + w[i]);
f[i][0] = max(f[i - 1][1], f[i - 1][0]);
}
cout << max(f[n][0], f[n][1]) << endl;
}
股票买卖 IV
给定一个长度为
的数组,数组中的第 个数字表示一个给定股票在第 天的价格。 设计一个算法来计算你所能获取的最大利润,你最多可以完成
笔交易。 注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
一次买入卖出合为一笔交易
题解:线性
- 状态表示
代表只在前 天中选择,且已经完成 笔交易,且 代表在第 天手中有股票, 代表第 天手中没有股票的最大收益
状态属性:
状态计算:
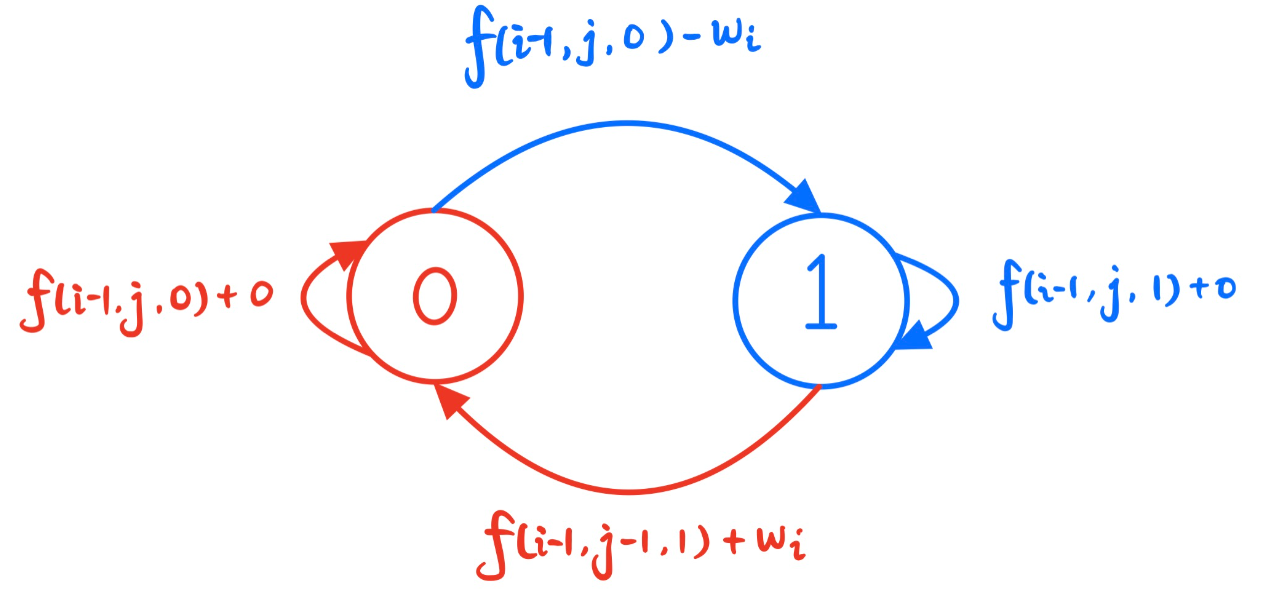
- 如果第
天手中有股票: - 如果第
天手中无股票:
- 状态优化:
因为是线性的,所以容易发现第一维可以优化掉,倒序遍历交易数量(第二维)
状态初始:
答案呈现:
const int N = 2e5 + 10, M = 1e2 + 10;
int n, m;
int w[N];
int f[M][2];
// f[i][j][0/1]代表只在前i天中选择,且已经完成j笔交易,且1代表在第i天手中有股票,0代表第i天手中没有股票的最大收益
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i)
cin >> w[i];
memset(f, -0x3f, sizeof f);
f[0][0] = 0;
for (int i = 1; i <= n; ++i)
for (int j = m; j >= 0; --j)
{
f[j][1] = max(f[j][1], f[j][0] - w[i]);
if (j >= 1)
f[j][0] = max(f[j][0], f[j - 1][1] + w[i]);
}
int ans = -INF;
for (int j = 0; j <= m; ++j)
ans = max({ans, f[j][0], f[j][1]});
cout << ans << endl;
}
股票买卖Ⅴ
给定一个长度为
的数组,数组中的第 个数字表示一个给定股票在第 天的价格。 设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为
天)。
题解:线性
- 状态表示:
:代表只在前 天中选,且 代表第 天手中有股票,1代表第 天是卖出股票后的第一天,2代表第 天卖出股票后的第 天( )能够获得的最大利润
状态属性:
状态计算:
状态机出口:
状态机入口:
状态初始:
答案呈现:
const int N = 2e5 + 10, M = 1e2 + 10;
int n;
int w[N];
int f[N][3];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> w[i];
for (int i = 0; i <= n; ++i)
f[i][1] = f[i][0] = -INF;
f[0][2] = 0;
for (int i = 1; i <= n; ++i)
{
f[i][0] = max(f[i - 1][0], f[i - 1][2] - w[i]);
f[i][1] = f[i - 1][0] + w[i];
f[i][2] = max(f[i - 1][1], f[i - 1][2]);
}
cout << max(f[n][1], f[n][2]) << endl;
}
设计密码
你现在需要设计一个密码
, 需要满足:
的长度是 ; 只包含小写英文字母; 不包含子串 ; 例如:
和 是 的子串, 不是 的子串。 请问共有多少种不同的密码满足要求?
由于答案会非常大,请输出答案模
的余数。
题解:
- 状态表示:
:代表已经生成了 位密码,且第 位密码已经匹配到子串中位置为 ,即第 位密码正在和子串中 位进行匹配的方案数 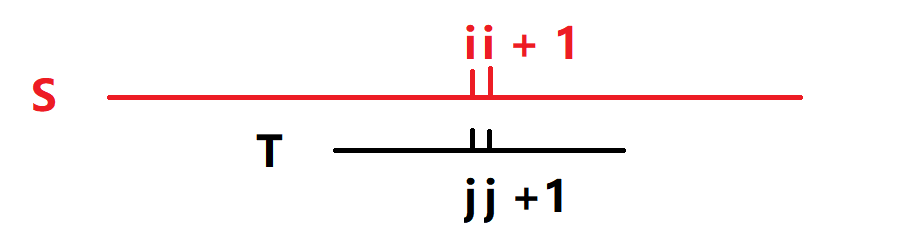
状态属性:数量
状态转移:
因为字符串
中只存在小写字母,所以S的位置 处的字符只有 种可能性 我们不妨枚举位置
会出现的所有小写字母 如果第
位的字母k不等于 ,我们总可以利用 的 数组找到一个位置 使得 我们令
,字符串 的长度为 ,因为 中不能含有 ,所以只有 的时候才能转移 状态转移方程:
时间复杂度:
状态初始:
答案呈现:
const int N = 50 + 10, M = 4e5 + 10;
int n;
int ne[N];
int f[N][N];
void solve()
{
cin >> n;
string t;
cin >> t;
int m = t.length();
t = " " + t;
ne[1] = 0;
for (int i = 2, j = 0; i <= m; ++i)
{
while (j && t[i] != t[j + 1])
j = ne[j];
if (t[i] == t[j + 1])
j++;
ne[i] = j;
}
f[0][0] = 1;
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
for (char k = 'a'; k <= 'z'; ++k)
{
int u = j;
while (u && t[u + 1] != k)
u = ne[u];
if (t[u + 1] == k)
u++;
if (u < m)
f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;
}
int ans = 0;
for (int j = 0; j < m; ++j)
ans = (ans + f[n][j]) % mod;
cout << ans << endl;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 单线程的Redis速度为什么快?
· 展开说说关于C#中ORM框架的用法!
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Pantheons:用 TypeScript 打造主流大模型对话的一站式集成库
· SQL Server 2025 AI相关能力初探