AtCoder Beginner Contest 296
Transition Game
给定序列\(a\),\(1<=a_i<=n\),一场游戏有\(n\)个回合,第\(i\)回合时,第一个人先指定一个任意数\(k\),第二个人任意选定一个\(x\),\(1<=x<=n\),然后\(x:=a_x\)执行\(k\)次,如果最后\(x=i\),那么第二个人获胜,否则第一个人获胜
对于\(n\)个回合,求出第二个人能够赢得的回数
题解:拓扑排序 + 思维
我们发现对于任意数\(k\)来说,只要当前回合\(i\)能够在序列\(a\)上形成一个闭环,就说明第二个人一定能胜,所以实际上对于所有回合来说是一个有向图,我们不妨利用拓扑排序求出有哪些点形成了闭环,那么在形成闭环的这些点上第二个人都会胜
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
int n;
int a[N];
queue<int> q;
int du[N];
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
}
int ans = 0;
for (int i = 1; i <= n; ++i)
{
du[a[i]]++;
}
int cnt = 0;
for (int i = 1; i <= n; ++i)
{
if (du[i] == 0)
q.push(i);
}
while (q.size())
{
int u = q.front();
q.pop();
cnt++;
for (auto v : g[u])
{
du[v]--;
if (du[v] == 0)
q.push(v);
}
}
cout << n - cnt << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
Simultaneous Swap
给定两个序列\(a,b\),每次操作选择\([1,n]\)中三个成对不同的整数\(i,j,k\),然后交换\(a_i,a_j\),再交换\(a_i,a_k\),询问两个序列在经过任意操作后是否会变得相同
题解:思维 + 逆序对 : 好题目
引理:
- 如果一个序列中元素不重复,那么交换任意两个元素,该排列的奇偶性一定会改变
- 对于任意一个排列,总可以经过一定交换使得该排列变成标准排列,且交换的次数的奇偶性和排列的奇偶习惯相同
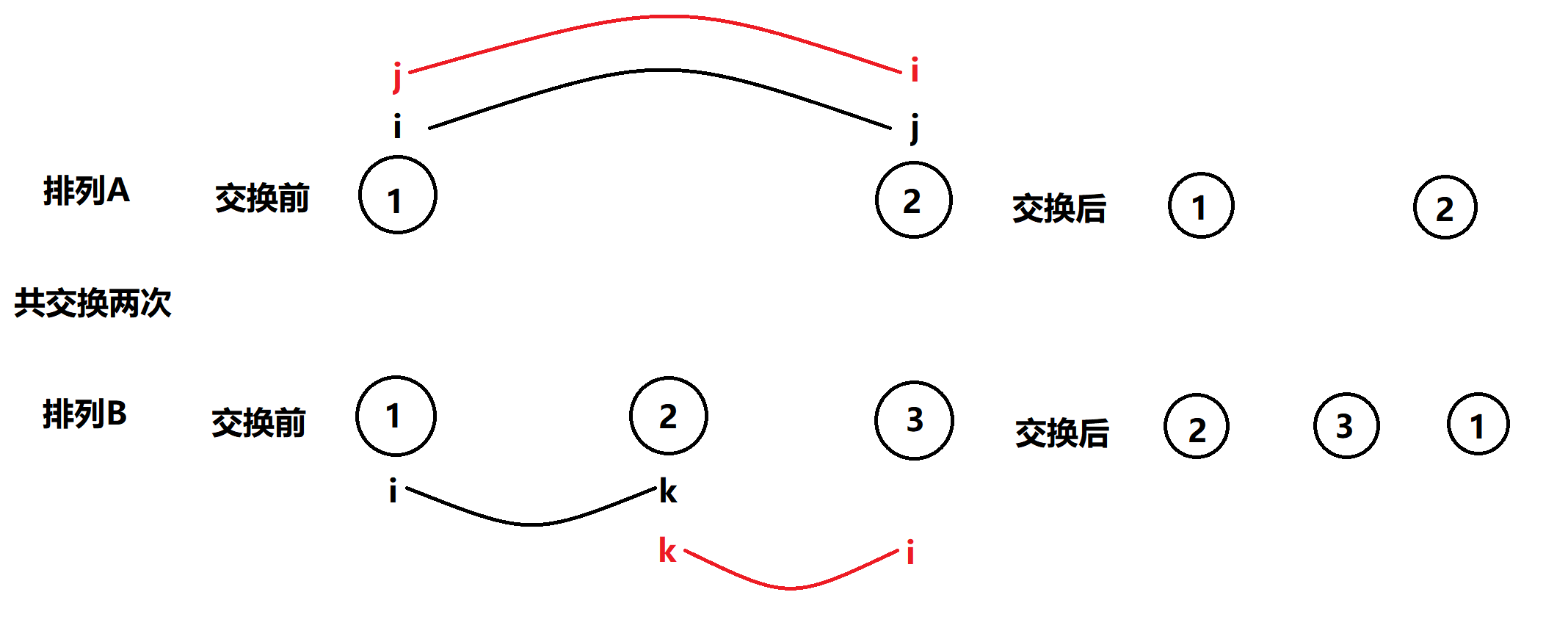
我们考虑一个这样的操作:
我们发现对于这样的交换不会改变两个排列的奇偶性,并且能够保证使得一个排列不改变原有元素的位置,另一个排列相当于做了一次周期为\(3\)的轮换,所以我们不妨先将排列\(a\)任意交换成标准排列,同时排列\(b\)同步更新,这样并不会改变排列\(a\)和排列\(b\)之间的奇偶性关系;
那么现在排列\(a\)是标准排列,且是偶排列。
- 如果排列\(b\)是偶排列,我们一定能通过上面的操作在不改变排列\(a\)和不改变排列b的奇偶性情况下,使得排列\(b\)也变成标准排列
- 如果排列\(b\)是奇排列,可以推断出我们无法使得\(b\)变成标准排列,但是如果存在两个以上相同的元素,我们可以在上述的操作中交换两个相同的元素,然后再交换不同的元素使得排列\(b\)变为偶排列,那么排列\(b\)也能够变成标准排列
所以我们得到结论:
- 如果两个排列的奇偶性一样,一定能够通过交换使得两个排列相同
- 如果两个排列的奇偶性不一样,但是如果一个排列中存在两个以上相同的元素,一定能够通过交换使得两个排列相同
- 如果两个排列相同的元素其对应的数量不一样,肯定无法完成
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
int n;
int c[N];
int a[N], b[N];
unordered_map<int, int> mp;
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
while (x <= n)
{
c[x] += val;
x += lowbit(x);
}
}
int get_sum(int x)
{
int res = 0;
while (x > 0)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int query(int l, int r)
{
return get_sum(r) - get_sum(l - 1);
}
void solve()
{
cin >> n;
int cnt1 = 0, cnt2 = 0;
bool flag = false;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
cnt1 += query(a[i] + 1, n);
add(a[i], 1);
mp[a[i]]++;
if (mp[a[i]] >= 2)
flag = true;
}
for (int i = 1; i <= n; ++i)
c[i] = 0;
for (int i = 1; i <= n; ++i)
{
cin >> b[i];
cnt2 += query(b[i] + 1, n);
add(b[i], 1);
mp[b[i]]--;
}
for (auto [x, y] : mp)
{
if (y != 0)
{
cout << "No" << endl;
return;
}
}
if (cnt1 % 2 == cnt2 % 2 || flag == true)
cout << "Yes" << endl;
else
cout << "No" << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}