2016GPLT
排座位
从1到
N编号;M为已知两两宾客之间的关系数;K为查询的条数。随后M行,每行给出一对宾客之间的关系,格式为:宾客1 宾客2 关系,其中关系为1表示是朋友,-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行,每行给出一对需要查询的宾客编号,如果两位宾客之间是朋友,且没有敌对关系,则输出No problem;如果他们之间并不是朋友,但也不敌对,则输出OK;如果他们之间有敌对,然而也有共同的朋友,则输出OK but...;如果他们之间只有敌对关系,则输出No way
题解:并查集
首先如果两人之间不可能既是朋友,又是敌人,所以只要判断两人是不是敌对关系,如果是敌对关系我们需要看看有没有共同的朋友,那么我们可以将存在朋友关系的人利用并查集合并到一个集合中,直接查询即可
#include <bits/stdc++.h>
#include <unordered_set>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e2 + 10, M = 4e5 + 10;
int n, m, k;
int p[N][N];
int fa[N];
int find(int x)
{
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void merge(int u, int v)
{
u = find(u);
v = find(v);
if (u != v)
fa[u] = v;
}
void solve()
{
cin >> n >> m >> k;
for (int i = 1; i <= n; ++i)
fa[i] = i;
for (int i = 1; i <= m; ++i)
{
int u, v, x;
cin >> u >> v >> x;
p[u][v] = p[v][u] = x;
if (x == 1)
merge(u, v);
}
while (k--)
{
int u, v;
cin >> u >> v;
if (p[u][v] == 1)
cout << "No problem" << endl;
else if (p[u][v] == 0)
cout << "OK" << endl;
else if (p[u][v] == -1)
{
if (find(u) == find(v))
cout << "OK but..." << endl;
else
cout << "No way" << endl;
}
}
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
玩转二叉树
给定二叉树的中序遍历和前序遍历,将树做镜面反转后,再输出反转后的层序遍历,镜面反转就是将所有非叶子节点的左右孩子互换
题解:二叉树的遍历
我们发现镜面反转无非是先遍历右儿子再遍历左儿子
我们再考虑如何根据二叉树的中序遍历和前序遍历来输出层序遍历:
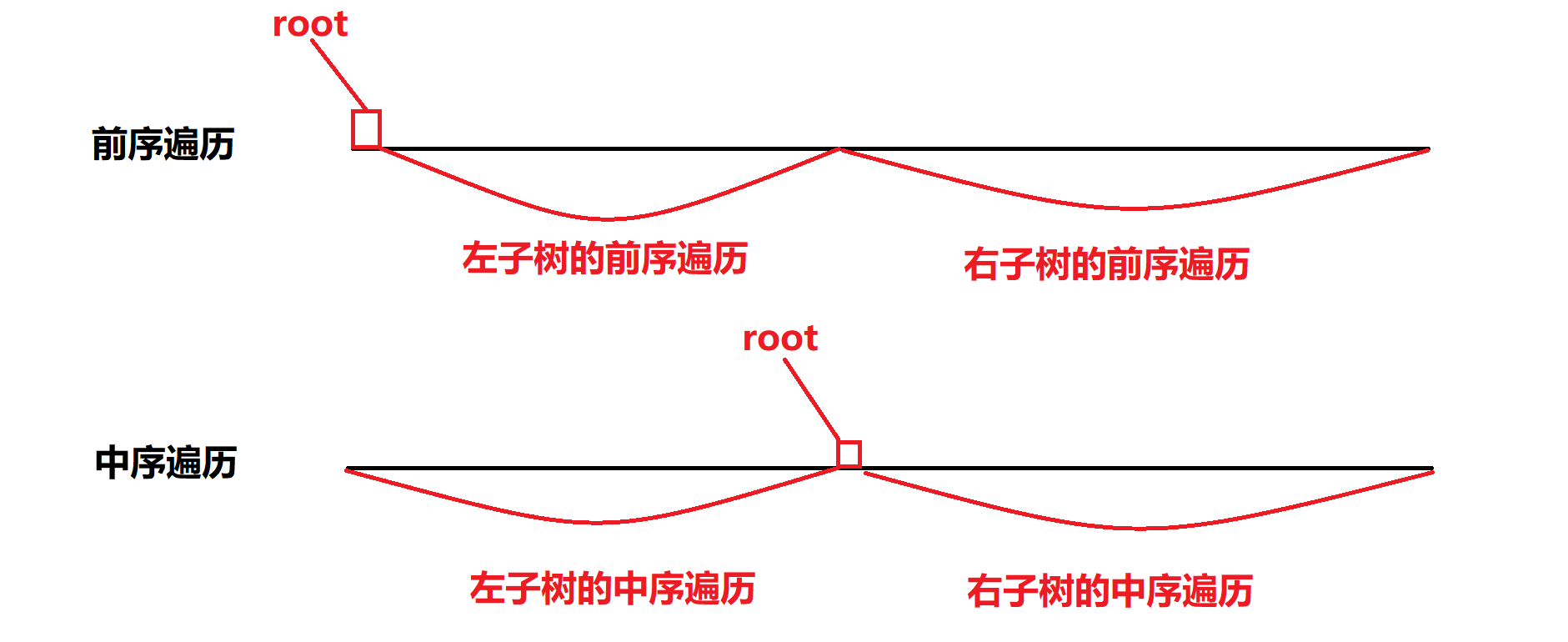
- 首先中序遍历是左根右的顺序,前序遍历是根左右的顺序,我们模拟过程尝试递归解决该问题
我们发现我们可以递归解决该问题:因为根节点一定是前序遍历的第一个点,我们只要在中序遍历中找到根节点,然后我们就知道了左子树和右子树相对应的前序遍历和中序遍历,因为前序遍历和中序遍历长度一定是一样的,我们可以从中序遍历的长度反推出前序遍历的长度
那么输出层序遍历就是用数组存储二叉树,注意左儿子和右儿子存放的位置应该交换
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
int n;
int tree[N];
int pre[N]; // 前序遍历
int in[N]; // 中序遍历
void dfs(int rt_index, int l, int r, int id)
{
if (l > r)
return;
int rt = pre[rt_index];
tree[id] = rt;
int p = 0;
for (int i = l; i <= r; ++i)
if (in[i] == rt)
{
p = i;
break;
}
dfs(rt_index + 1, l, p - 1, id * 2 + 1);
dfs(rt_index + p - l + 1, p + 1, r, id * 2);
}
void solve()
{
memset(tree, -1, sizeof tree);
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> in[i];
for (int i = 1; i <= n; ++i)
cin >> pre[i];
dfs(1, 1, n, 1);
int cnt = 0;
for (int i = 1; cnt < n; i++)
{
if (tree[i] != -1)
{
cout << tree[i] << " ";
cnt++;
}
}
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
关于堆的判断
将一系列给定数字顺序插入一个初始为空的小顶堆
H[]。随后判断一系列相关命题是否为真。命题分下列几种:
x is the root:x是根结点;x and y are siblings:x和y是兄弟结点;x is the parent of y:x是y的父结点;x is a child of y:x是y的一个子结点;- 对输入的每个命题,如果其为真,则在一行中输出
T,否则输出F。
题解:模拟堆:\(O(nlogn)\)
根据题意我们模拟小根堆,我们将所有的数插入堆\(O(nlogn)\)后利用哈希表记录每个数字在数组上下标的映射,然后\(O(1)\)回答询问即可
int n, q;
int idx;
int h[N];
unordered_map<int, int> mp;
void down(int u)
{
int t = u;
if (u * 2 <= idx && h[u * 2] < h[t])
t = u * 2;
if (u * 2 + 1 <= idx && h[u * 2 + 1] < h[t])
t = u * 2 + 1;
if (t != u)
{
swap(h[t], h[u]);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u / 2] > h[u])
{
swap(h[u / 2], h[u]);
u /= 2;
}
}
void solve()
{
cin >> n >> q;
for (int i = 1; i <= n; ++i)
{
int x;
cin >> x;
h[++idx] = x;
up(idx);
}
for (int i = 1; i <= n; ++i)
mp[h[i]] = i;
while (q--)
{
string s;
int x, y;
cin >> x;
cin >> s;
if (s == "and")
{
cin >> y;
cin >> s >> s;
if (mp[x] / 2 == mp[y] / 2)
cout << "T" << endl;
else
cout << "F" << endl;
}
else
{
cin >> s;
if (s == "a")
{
cin >> s >> s >> y;
if (mp[x] / 2 == mp[y])
cout << "T" << endl;
else
cout << "F" << endl;
}
else
{
cin >> s;
if (s == "root")
{
if (mp[x] == 1)
cout << "T" << endl;
else
cout << "F" << endl;
}
else
{
cin >> s >> y;
if (mp[y] / 2 == mp[x])
cout << "T" << endl;
else
cout << "F" << endl;
}
}
}
}
}
天梯地图
输入在第一行给出两个正整数
N(2 ≤N≤ 500)和M,分别为地图中所有标记地点的个数和连接地点的道路条数。随后M行,每行按如下格式给出一条道路的信息:V1 V2 one-way length time其中
V1和V2是道路的两个端点的编号(从0到N-1);如果该道路是从V1到V2的单行线,则one-way为1,否则为0;length是道路的长度;time是通过该路所需要的时间。最后给出一对起点和终点的编号。输出格式:
首先按下列格式输出最快到达的时间
T和用节点编号表示的路线:Time = T: 起点 => 节点1 => ... => 终点然后在下一行按下列格式输出最短距离
D和用节点编号表示的路线:Distance = D: 起点 => 节点1 => ... => 终点如果最快到达路线不唯一,则输出几条最快路线中最短的那条,题目保证这条路线是唯一的。而如果最短距离的路线不唯一,则输出途径节点数最少的那条,题目保证这条路线是唯一的。
如果这两条路线是完全一样的,则按下列格式输出:
Time = T; Distance = D: 起点 => 节点1 => ... => 终点
题解:单源最短路求方案 + 多种限制
显然我们需要跑两个不同的\(dij\),一个用来求出最短距离,一个用来求出最短时间,我们考虑如何记录方案,显然我们可以记录一个点的前驱,所以不妨借用\(dp\)的思想开个\(pre\)前驱数组来记录每次的转移
那么方案的问题解决了,我们考虑题目给出的限制已经在这个限制上我们状态怎么转移
- 最短距离的基础上求经过的点最少,显然我们的前驱数组的\(size\)就是经过的点数,如果最短距离相同的情况下,我们比较一下前驱数组的大小,选择小的转移即可
- 最短时间的基础上求经过的距离最短,我们同时还需要一个\(dis\)数组,和最短时间一起同步更新,如果下一个点在最短时间相同的情况下,我们比较一下\(dis[v]>dis[u] + w\)即可
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 5e2 + 10, M = 4e5 + 10;
int n, m;
vector<array<int, 3>> g[N];
int d1[N], d2[N];
vector<int> dij1(int st, int ed) // 时间
{
for (int i = 0; i < n; ++i)
d1[i] = INF;
vector<int> pre[N];
vector<int> vis(n + 10);
vector<int> dis(n + 10);
d1[st] = 0;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({d1[st], st});
while (q.size())
{
int u = q.top().second;
q.pop();
if (vis[u])
continue;
vis[u] = 1;
for (auto &[v, w1, w2] : g[u])
{
if (d1[v] > d1[u] + w1)
{
d1[v] = d1[u] + w1;
dis[v] = dis[u] + w2; //同步更新
pre[v] = pre[u];
pre[v].push_back(u);
q.push({d1[v], v});
}
else if (d1[v] == d1[u] + w1 && dis[v] > dis[u] + w2)
{
pre[v] = pre[u];
pre[v].push_back(u);
}
}
}
pre[ed].push_back(ed);
return pre[ed];
}
vector<int> dij2(int st, int ed) // 距离
{
for (int i = 0; i < n; ++i)
d2[i] = INF;
vector<int> pre[N];
vector<int> vis(n + 10);
d2[st] = 0;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({d2[st], st});
while (q.size())
{
int u = q.top().second;
q.pop();
if (vis[u])
continue;
vis[u] = 1;
for (auto &[v, w1, w2] : g[u])
{
if (d2[v] > d2[u] + w2)
{
d2[v] = d2[u] + w2;
pre[v] = pre[u];
pre[v].push_back(u);
q.push({d2[v], v});
}
else if (d2[v] == d2[u] + w2 && pre[v].size() > pre[u].size() + 1)
{
pre[v] = pre[u];
pre[v].push_back(u);
}
}
}
pre[ed].push_back(ed);
return pre[ed];
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= m; ++i)
{
int u, v, flag, len, time;
cin >> u >> v >> flag >> len >> time;
if (flag)
{
g[u].push_back({v, time, len});
}
else
{
g[u].push_back({v, time, len});
g[v].push_back({u, time, len});
}
}
int st, ed;
cin >> st >> ed;
auto ans1 = dij1(st, ed);
auto ans2 = dij2(st, ed);
if (ans1 == ans2)
{
cout << "Time = " << d1[ed] << "; Distance = " << d2[ed] << ": ";
for (int i = 0; i < ans1.size(); i++)
{
if (i != 0)
cout << " => ";
cout << ans1[i];
}
cout << endl;
}
else
{
cout << "Time = " << d1[ed] << ": ";
for (int i = 0; i < ans1.size(); i++)
{
if (i != 0)
cout << " => ";
cout << ans1[i];
}
cout << endl;
cout << "Distance = " << d2[ed] << ": ";
for (int i = 0; i < ans2.size(); i++)
{
if (i != 0)
cout << " => ";
cout << ans2[i];
}
cout << endl;
}
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}