数论基础
高精度
高精度加法
vector<int> add(vector<int> &a, vector<int> &b)
{
vector<int> c;
int t = 0; // 代表进位
for (int i = 0; i < a.size() || i < b.size(); ++i)
{
if (i < a.size())
t += a[i];
if (i < b.size())
t += b[i];
c.push_back(t % 10);
t /= 10;
}
if (t)
c.push_back(1);
return c;
}
高精度减法
bool cmp(vector<int> &a, vector<int> &b) // 判断a和b大小
{
if (a.size() != b.size())
return a.size() > b.size();
for (int i = a.size() - 1; i >= 0; --i) //从高位开始比较
{
if (a[i] != b[i])
return a[i] > b[i];
}
return true; // a = b
}
vector<int> sub(vector<int> &a, vector<int> &b)
{
vector<int> c;
int t = 0; // 代表借位
for (int i = 0; i < a.size(); ++i)
{
t = a[i] - t;
if (i < b.size())
t -= b[i];
c.push_back((t + 10) % 10);
if (t < 0) // 有借位
t = 1;
else // 没有借位
t = 0;
}
while (c.size() > 1 && c.back() == 0) // 去除前导0
c.pop_back();
return c;
}
void solve()
{
string a, b;
cin >> a >> b;
vector<int> A, B, C;
for (int i = a.size() - 1; i >= 0; i--)
A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; i--)
B.push_back(b[i] - '0');
if (cmp(A, B)) // a >= b ==> C = A - B
{
C = sub(A, B);
for (int i = C.size() - 1; i >= 0; i--)
cout << C[i];
}
else // a < b ==> C = - (B - A)
{
C = sub(B, A);
cout << "-";
for (int i = C.size() - 1; i >= 0; i--)
cout << C[i];
}
}
高精度乘低精度
vector<int> mul(vector<int> &a, int b)
{
vector<int> c;
int t = 0; // 表示进位
for (int i = 0; i < a.size() || t; ++i)
{
if (i < a.size())
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (c.size() > 1 && c.back() == 0) // 若b = 0,去除前导0
c.pop_back();
return c;
}
高精度乘高精度\(O(n^2)\)
vector<int> mul(vector<int> &a, vector<int> &b)
{
vector<int> c(a.size() + b.size() + 10); //注意容量需要稍大一点
for (int i = 0; i < a.size(); ++i)
for (int j = 0; j < b.size(); ++j)
c[i + j] += a[i] * b[j];
int t = 0; // 表示进位
for (int i = 0; i < c.size() || t; ++i)
{
t += c[i];
c[i] = t % 10;
t /= 10;
}
while (c.size() > 1 && c.back() == 0) // 去除前导0
c.pop_back();
return c;
}
高精度除低精度
vector<int> div(vector<int> &a, int b, int &r) // C = A / b ... r
{
vector<int> c;
r = 0; // 余数
for (int i = a.size() - 1; i >= 0; i--) // 从高位开始处理
{
r = r * 10 + a[i];
c.push_back(r / b);
r %= b;
}
reverse(c.begin(), c.end()); // C原本是高位在前面,但是为了去除前导0,需要反转
while (c.size() > 1 && c.back() == 0) // 去除前导0
c.pop_back();
return c;
}
高精度除高精度
质数
判断质数(试除法)\(O(\sqrt{n})\)
如果\(d|n\)则\(\frac{n}{d}|n\),所以我们只要枚举\(i<=\frac{n}{i}\)即可
bool is_prime(int x)
{
if (x < 2)
return false;
for (int i = 2; i <= n / i; ++i)//注意最好是i<=n/i,如果是i*i<=n会有溢出风险
{
if (n % i == 0)
return false;
}
return true;
}
分解质因数\(O(\sqrt{n})\)
引理:\(n\)中最多只包含一个大于\(\sqrt{n}\)的质因子,因为,如果有两个的话肯定会超过\(n\)
所以我们只要枚举所有小于\(\sqrt{n}\)的因子即可,最后,如果\(n\)还有剩余,那么这个肯定是唯一大于\(\sqrt{n}\)的质因子
vector<int> vec;
void divide(int x)
{
for (int i = 2; i <= n / i; ++i)
{
if (n % i == 0)
{
vec.push_back(i);
while (n % i == 0)
n /= i;
}
}
if (n > 1)
vec.push_back(n);
}
阶乘分解质因数
举个例子:\(12!=12\times 11 \times 10 \times 9 \times 8 ... 2 \times 1\)
假设我们想知道\(12!\)中质因子\(2\)的个数:
- 首先我们发现\(2\)的倍数中\((2,4,6,8,10,12)\)一定有质因子\(2\),他们的个数为\(12/2=6\)
- 其次我们又发现\(4\)的倍数中\((4,8,12)\)还有一个\(2\)没有被加入贡献,他们的个数为\(12/4=3\)
- 我们又发现\(8\)的倍数中\((8)\)还有一个\(2\)没有被加入贡献,他们的个数为\(12/8=1\)
所以我们推导得:阶乘\(n!\)中某个质因子\(p\)的幂次为
\[\lfloor \frac{n}{p} \rfloor + \lfloor \frac{n}{p^2} \rfloor + \lfloor \frac{n}{p^3} \rfloor + ... + \lfloor \frac{n}{p^k} \rfloor \]时间复杂度为\(O(log_pn)\)
int get(int n, int p)
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
欧拉筛质数(线性筛法)\(O(n)\)
注意所有的合数只能被其最小的质因子筛掉
int prime[N], tot = 1;
int vis[N];
void get_prime(int n)
{
for (int i = 2; i <= n; ++i)
{
if (!vis[i])
prime[tot++] = i;
for (int j = 1; j < tot && prime[j] * i <= n; ++j)
{
vis[prime[j] * i] = 1;
if (i % prime[j] == 0) //使得合数只能被其最小质因子筛掉,防止了重复标记
break;
}
}
}
约数
求所有约数(试除法)\(O(\sqrt{n})\)
vector<int> vec;
void get_divisors(int n)
{
for (int i = 1; i <= n / i; ++i)
{
if (n % i == 0)
{
vec.push_back(i);
if (i != n / i) //防止i*i=n
vec.push_back(n / i);
}
}
}
求约数个数和约数之和
引申:\(n=p_1^{\alpha_1}p_2^{\alpha_2}p_3^{\alpha_3}...p_k^{\alpha_k}\),任取n的任意一个约数\(d\),\(d=p_1^{\beta_1}p_2^{\beta_2}p_3^{\beta_3}...p_k^{\beta_k},0<=\beta_i<=\alpha_i\)
所以n的约数的个数一定为\((\alpha_1+1)(\alpha_2+1)(\alpha_3+1)...(\alpha_k+1)\)
引申:\(int\)范围内约数个数约等于\(1500\)
n的约数之和为\((p_1^{0}+p_1^{1}+...+p_1^{\alpha_1})*(p_2^{0}+p_2^{1}+...+p_2^{\alpha_2})*(p_3^{0}+p_3^{1}+...+p_3^{\alpha_3})...(p_k^{0}+p_k^{1}+...+p_k^{\alpha_k})\)
int n;
for (int i = 2; i <= n / i; ++i)
{
while (n % i == 0)
{
mp[i]++; //存放质因子的幂次
n /= i;
}
}
if (n > 1)
mp[n]++;
int ans = 1; //求约数之和
for (auto [x, y] : mp)
{
int res = 1;
while (y--)
res = (res * x + 1) % mod; //t=1,t=p+1,t=p^2+p+1...t=p^a+p^(a-1)...+1
ans = ans * res % mod;
}
求约数之和Ⅱ \(O(nlogn)\)
设\(d(n)\)为\(n\)的约数之和,求出\(i∈[1,n]\)中所有\(d(i)\)
引理:调和级数:\(n+\frac{n}{2}+\frac{n}{3}+...+\frac{n}{n}=nlogn\)
for (int i = 1; i <= n; ++i)
for (int j = i; j <= n; j += i)
d[j] += i;
欧拉函数
求欧拉函数\(O(\sqrt n)\)
我们定义\(1-n\)中与\(n\)互质的数的个数成为欧拉函数,记作\(\varphi(n)\)
我们可以知道,通过质因子分解我们可以得到:\(n=p_1^{\alpha_1}p_2^{\alpha_2}p_3^{\alpha_3}...p_k^{\alpha_k}\)
结论:\(\varphi(n) = n*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_k})\)
证明:利用容斥原理证明
我们先减去\(p_1,p_2,...p_k\)的所有倍数:\(n-\frac{n}{p_1}-\frac{n}{p_2}...-\frac{n}{p_k}\)
因为\(p_1*p_2,p_1*p_3,...p_1*p_k,p_2*p_3...p_2*p_k\)这些倍数在上面被多删了\(1\)次,所以我们需要加回来:
\(n-\frac{n}{p_1}-\frac{n}{p_2}...-\frac{n}{p_k}+\frac{n}{p_1*p_2}+\frac{n}{p_1*p_3}+...+\frac{n}{p_{k-1}*p_k}\)
同理我们三个数的倍数在上面1减1加后实际上没有改变,所以我们对三个数的倍数需要减去1次
同理四个数我们需要加上
以此类推
最后我们发现将公式整理后得到我们刚才的结论:\(\varphi(n) = n*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_k})\)
int res = n;
for (int i = 2; i <= n / i; ++i)
{
if (n % i == 0)
{
while (n % i == 0)
n /= i;
res = res * (i - 1) / i;
}
}
if (n > 1)
res = res * (n - 1) / n;
cout << res << endl;
欧拉筛求欧拉函数\(O(n)\)
给定正整数\(n\),求\(1-n\)中每个数的欧拉函数\(\varphi(i)\),并且求出\(\sum_{i=1}^{n}\varphi(i)\)
我们可以在欧拉筛中顺便求出\(\varphi(i)\)
如果某个数\(i\)是质数,那么\(\varphi(i)=i-1\)
我们在去除合数的过程中:
如果\(prime[j]\)是\(i\)的最小质因子,即\(i\%prime[j]==0\),我们可以得到:
$\varphi(i) = i*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_k})$ $\varphi(prime[j]*i) = prime[j]*i*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_k})$所以:\(\varphi(prime[j]*i) = prime[j]*\varphi(i)\)
如果\(prime[j]\)不是\(i\)的最小质因子,即\(i\%prime[j]!=0\),我们可以得到:
$\varphi(i) = i*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_k})$ $\varphi(prime[j]*i) = prime[j]*i*(1-\frac{1}{p_1})*(1-\frac{1}{p_2})*...*(1-\frac{1}{p_k})*(1-\frac{1}{prime[j]})$ 所以:$\varphi(prime[j]*i) = prime[j]*\varphi(i)*(1-\frac{1}{prime[j]})=(prime[j]-1)*\varphi(i)$\(\varphi(1)=1\)
int n;
int phi[N];
int p[N], vis[N];
int idx;
void get_euler(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; ++i)
{
if (!vis[i])
{
p[++idx] = i;
phi[i] = i - 1;
}
for (int j = 1; j <= idx && p[j] * i <= n; ++j)
{
vis[p[j] * i] = 1;
if (i % p[j] == 0)
{
phi[p[j] * i] = p[j] * phi[i];
break;
}
else
phi[p[j] * i] = (p[j] - 1) * phi[i];
}
}
int res = 0;
for (int i = 1; i <= n; ++i)
{
cout << phi[i] << " ";
}
cout << res << endl;
}
快速幂 \(O(logn)\)
int qpow(int a, int b)
{
int res = 1;
while (b)
{
if (b & 1)
res *= a;
a *= a;
b >>= 1;
}
return res;
}
快速幂求乘法逆元
给定\(b\),\(p\),其中\(p\)是质数,求\(b\)在模\(p\)下的乘法逆元,若逆元不存在输出impossible
费马小定理
给定\(a\),\(p\),且\(a\)和\(p\)互质,且\(p\)为质数,则\(a^p\equiv a(mod\ p)\), 即\(a^{p-1}\equiv 1(mod\ p)\)
乘法逆元
若整数\(b\),\(m\)互质,且\(m\)为质数,对于任意整数\(a\),如果满足\(b|a\),则存在一个正整数\(x\),使得\(a/b\equiv a*x(mod \ m)\),我们称\(x\)是\(b\)在模\(m\)下的乘法逆元
结论:\(b\)存在乘法逆元的充要条件是\(b\)和模数\(m\)互质,且当模数\(m\)为质数时,则\(b^{p-2}\)即为\(b\)的乘法逆元
简单证明:
- \(a/b\equiv a*x(mod\ m)\)
- \(a\equiv a*b*x(mod\ m)\)
- \(b*x\equiv 1(mod \ m)\)
- 根据费马小定理:\(b^{p-1} \equiv 1(mod \ p)\)
- \(b*x = b^{p-1}\)
- \(x = b^{p-2}\)
所以如果\(b\)和\(m\)互质就代表\(b\)存在乘法逆元\(x\),\(x=b^{p-2}\),否则\(b\)不存在乘法逆元
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int qpow(int a, int b, int p)
{
int res = 1;
while (b)
{
if (b & 1)
res = res * a % p;
b >>= 1;
a = a * a % p;
}
return res % p;
}
void solve()
{
int n;
cin >> n;
while (n--)
{
int a, p;
cin >> a >> p;
if (gcd(a, p) == 1)
cout << qpow(a, p - 2, p) << endl;
else
cout << "impossible" << endl;
}
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
欧几里得算法\(O(logn)\)
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
裴蜀定理
- 对方程\(ax+by=c且a,b,c∈Z\),如果满足\(gcd(a,b)|c\),那么该方程一定有整数解
- 对于任意正整数\(a,b\),一定存在非零整数\(x,y\),使得\(ax+by=gcd(a,b)\)
扩展欧几里得算法\(O(logn)\)
如果我们要研究\(ax+by=n\)的所有\(x\)、\(y\)解集,我们需要接下来三步:
1.我们判断\(ax+by=n\)有没有解,我们只需要去判断\(\frac{n}{gcd(a,b)}\)是不是整数,如果是整数说明有解,否则无解2.我们先去求出\(ax+by=gcd(a,b)\)的一组特解
我们利用递归来推导一下它的解:
首先我们知道\(gcd(a,0) = a\),这是递归的出口
因为\(ax_1+by_1=gcd(a,b),bx_2+(a\%b)y_2=gcd(b,a\%b)\)\(,gcd(a,b)=gcd(b,a\%b),\)
又因为\(a\%b=a-a/b*b\)
所以\(ax_1+by_1=bx_2+(a-a/b*b)y_2\)
化简得:\(ax_1+by_1=ay_2+b(x_2-a/b*y_2)\)
所以\(x_1 = y_2,y_1=x_2-a/b*y_2\)
我们只需要将\(x_2,y_2\)不断带入递归直到\(gcd=a\),即\(由ax+0y=a得到x=1,y=0,\)然后回溯即可得到特解\(x_0\),\(y_0\)那么\(ax+by=gcd(a,b)\)的通解就是:\(x=x_0+k*\frac{b}{gcd(a,b)},y=y_0+k*\frac{a}{gcd(a,b)},k为整数\)
3.我们将\(ax+by=gcd(a,b)\)的特解\(x_0\),\(y_0\)乘以\(\frac{n}{gcd(a,b)}\)就能得出\(ax+by=n\)的一组特解
那么\(ax+by=n\)的通解跟第二步一样
4.引申一下\(ax+by=n\)的最小正整数解\(x_1=(x\%\frac{b}{gcd(a,b)}+\frac{b}{gcd(a,b)})\%\frac{b}{gcd(a,b)}\)
我们可以注意到,当递归到递归出口时,\(b=0\),\(gcd(a,0)=a\)显然我们找到了\(a,b\)的最大公因数\(gcd(a,b)\),所以说扩展欧几里得算法也能计算最大公因数
int gcd(int a, int b) //欧几里得算法
{
return b == 0 ? a : gcd(b, a % b);
}
int exgcd(int a, int b, int &x, int &y) //扩展欧几里得算法
{
if (!b) //b==0,到达递归出口
{
x = 1;
y = 0;
return a; //返回最大公因数a
}
int d = exgcd(b, a % b, x, y); //向下递归
int t = x;
x = y;
y = t - a / b * y; //向上回溯
return d;
}
扩展欧几里得算法求解线性同余方程
对于方程 \(ax\equiv b(mod\ m)\),求是否存在\(int\)范围内整数解\(x\),如果没有解输出"impossible"
对于该方程我们可以将其形式转化为\((a*x)\%m=b\) ==> 存在整数\(y\)使得,\(ax = my+b\),即\(ax-my = b\)
显然对于转化之后的方程\(ax-my = b\),我们可以利用扩展欧几里得算法求解出\(x\)
- 判断是否有解:如果\(gcd(a,m)|b\),则代表有解(由裴蜀定理我们可以知道\(ax-my=gcd(a,m)\)一定存在整数解,所以只要\(b\)能够整除\(gcd(a,m)\),就代表存在解)
- 如果有解,则利用扩展欧几里得算法求出\(ax-my=gcd(a,m)\)的特解\(x_0\),然后只要将\(x_0:=x_0*(b/d)\)即可,但是题目又要求\(x_0\)再\(int\)范围内,所以我们只需要\(x_0:=x_0\%m\)即可(因为取模的性质:\(a*(x\%m)=(a*x)\%m = b\))
#include <bits/stdc++.h>
using namespace std;
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define endl '\n'
#define int long long
int n;
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int t = x;
x = y;
y = t - a / b * y;
return d;
}
signed main()
{
cin >> n;
while (n--)
{
int a, b, x, y, m;
cin >> a >> b >> m;
int d = exgcd(a, m, x, y);
cout << d << endl;
if (b % d != 0)
cout << "impossible" << endl;
else
cout << x * (b / d) % m << endl;
}
return 0;
}
模运算
负数取模
不断对负数加上模数直到成为正数后正常取模即可
取模的性质
- 取模的加法性质:\((a+b)\%m = (a\%m+b\%m)\%m\)
- 取模的乘法性质:\(a*b\%m = (a\%m*b\%m)\%m\)
- 求最小正整数解:\((a\%m+m)\%m\)
中国剩余定理\(O(nlogm)\)
给定\(n\)个线性同余方程,
\[\begin{equation} \left\{ \begin{array}{lr} x\equiv a_1 (mod\ m_1) \\ x\equiv a_2 (mod\ m_2) \\ x\equiv a_3 (mod\ m_3) \\ ...\\ x\equiv a_n (mod\ m_n) \\ \end{array} \right. \end{equation} \]其中\(m_1,m_2,...,m_n\)之间两两互质
我们构造出方程的解:
设\(M = m_1m_2m_3...m_n\),\(M_i=\frac{M}{m_i}\),我们可以得到\(M_i\)和\(m_i\)互质,所以\(M_i\)在在模\(m_i\)下的逆元一定存在,所以我们设\(M_i^{-1}\)为\(M_i\)在模\(m_i\)下的逆元,即\(M_iM_i^{-1}\equiv 1(mod\ m_i)\),注意逆元我们既可以用扩展欧几里得算法解同余方程得到也可以通过快速幂得到
我们得到方程的解\(x=\sum_{i=1}^{n}a_iM_iM_i^{-1}\)
扩展中国剩余定理
给定\(n\)个线性同余方程,
\[\begin{equation} \left\{ \begin{array}{lr} x\equiv a_1 (mod\ m_1) \\ x\equiv a_2 (mod\ m_2) \\ x\equiv a_3 (mod\ m_3) \\ ...\\ x\equiv a_n (mod\ m_n) \\ \end{array} \right. \end{equation} \]其中\(m_1,m_2,...,m_n\)模数不互质,我们可以通过合并相邻两组方程的方式来逐步得到解:
我们先随便挑两组方程:
\[\begin{equation} \left\{ \begin{array}{lr} x\equiv a_1 (mod\ m_1) \\ x\equiv a_2 (mod\ m_2) \\ \end{array} \right. \end{equation} \]我们转化其形式得:
\[\begin{equation} \left\{ \begin{array}{lr} x = k_1a_1 + m_1 \\ x = k_2a_1 + m_2 \\ \end{array} \right. \end{equation} \]所以我们得到:
\[k_1a_1+m_1 = k_2a_2+m_2\\ k_1a_1-k_2a_2=m_2-m_1 \]那么我们可以利用裴蜀定理判断该方程是否有解,即\(gcd(a_1,a_2)|(m_2-m_1)\),如果有解我们可以利用扩展欧几里得算法求出该方程的特殊解\(k_1,k_2\),同时也得到了通解:
\[k_1 = k_1+k\frac{a_2}{gcd(a_1,a_2)}\\ k_2 = k_2+k\frac{a_1}{gcd(a_1,a_2)}\\ \]所以:
\[x = k_1a_1+m_1\\ x = (k_1+k\frac{a_2}{gcd(a_1,a_2)})a_1+m_1\\ x = k_1a_1+m_1+k\frac{a_1a_2}{gcd(a_1,a_2)}\\ x = k*lcm(a_1,a_2) + k_1a_1+m_1 \]那么两个方程就合并到了一起,令\(a_1'=lcm(a_1,a_2),m_1' = k_1a_1+m_1\),得到:
\[x = ka_1'+m_1' \]同时我们也得到了通解\(x_0\),令\(x_0=k_1a_1+m_1\)
\[x = x_0 + k*lcm(a_1,a_2)\\ x \equiv x_0 (mod\ \ lcm(a_1,a_2)) \]那么我们可以得到其最小正整数解为:
\[x = x_0 \% a \]那么对于\(n\)个线性同余方程来说,我们只需要合并\(n-1\)次即可
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
int n;
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int t = x;
x = y;
y = t - a / b * y;
return d;
}
void solve()
{
cin >> n;
bool flag = true;
int a1, a2, m1, m2;
cin >> a1 >> m1;
for (int i = 1; i <= n - 1; ++i)
{
cin >> a2 >> m2;
int k1, k2;
int d = exgcd(a1, a2, k1, k2);
if ((m2 - m1) % d != 0) //裴蜀定理判断线性同余方程是否有解
{
flag = false;
break;
}
k1 *= (m2 - m1) / d;
int t = a2 / d;
k1 = (k1 % t + t) % t; //求出最小正整数的k1,为了防止数据太大而导致溢出
m1 = k1 * a1 + m1;
a1 = lcm(a1, a2);
}
if (flag)
cout << (m1 % a1 + a1) % a1 << endl; //求出最小正整数解
else
cout << -1 << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
求组合数
杨辉三角递推式\(dp\) \(O(n^2)\)
\[C_a^b=C_{a-1}^b + C_{a-1}^{b-1} \]
for (int a = 1; a < N; ++a)
{
for (int b = 0; b <= a; ++b)
{
if (b == 0 || b == a)
c[a][b] = 1;
else
c[a][b] = (c[a - 1][b] % mod + c[a - 1][b - 1] % mod) % mod;
}
}
预处理阶乘和阶乘逆元\(O(nlogn)\)
\[1<=b<=a<=1e6\\ C_a^b=\frac{a!}{(a-b)!b!} \]我们预处理出阶乘,并利用快速幂预处理出每个阶乘的逆元,注意\(0!\)为1,且\(0!\)的逆元也为1,即:
\[C_a^b=\frac{a!}{(a-b)!b!} = a!*((a-b)!)^{-1}*(b!)^{-1} \]
//预处理
fact[0] = inv[0] = 1;
for (int i = 1; i < N; ++i)
{
fact[i] = fact[i - 1] * i % mod;
inv[i] = qpow(fact[i], mod - 2, mod);
}
//单次操作
int C(int a, int b, int p)
{
int res = 1;
for (int i = 1, j = a; i <= b; ++i, --j)
{
res = res * j % p;
res = res * qpow(i, p - 2, p) % p;
}
return res % p;
}
卢卡斯定理 \(O(log_pn*plogp)\)
\[1<=b<=a<=10^{18},1<=p<=1e6\\ C_a^b \equiv C_{a/p}^{b/p}*C_{a\%p}^{b\%p} \ (mod\ p)\\ or\\ C_a^b \equiv C_{a^{k}}^{b^{k}}C_{a^{k-1}}^{b^{k-1}}...C_{a^{1}}^{b^{1}}C_{a^{0}}^{b^{0}} (mod\ p)\\ \]证明:
引理:
\((1+x)^p \equiv 1+x^p\ (mod\ p)\)
\((1+x)^{p^a} \equiv 1+x^{p^a}\ (mod\ p)\)
- 首先将\(a,b\)转换为\(p\)进制 \(O(log_pn)\)
\(a = a^kp^k+a^{k-1}p^{k-1}+...+a^1p^1+a^0p^0\)
\(b = b^kp^k+b^{k-1}p^{k-1}+...+b^1p^1+b^0p^0\)
\[(1+x)^a=(1+x)^{a^kp^k+a^{k-1}p^{k-1}+...+a^1p^1+a^0p^0}\\ =(1+x)^{a^kp^k}(1+x)^{a^{k-1}p^{k-1}}...(1+x)^{a^{1}p^{1}}(1+x)^{a^{0}p^{0}}\\ \equiv (1+x^{p^k})^{a^k}(1+x^{p^{k-1}})^{a^{k-1}}...(1+x^{p^1})^{a^1}(1+x^{p^0})^{a^0}\ (mod\ p) \]
- 因为\(C_a^b\)是\((1+x)^a\)展开式中\(x^b\)的系数,且\(b = b^kp^k+b^{k-1}p^{k-1}+...+b^1p^1+b^0p^0\),所以
\[C_a^b \equiv C_{a^{k}}^{b^{k}}C_{a^{k-1}}^{b^{k-1}}...C_{a^{1}}^{b^{1}}C_{a^{0}}^{b^{0}} (mod\ p)\\ C_a^b \equiv C_{a^{k}}^{b^{k}}C_{a^{k-1}}^{b^{k-1}}...C_{a^{1}}^{b^{1}}C_{a_0\%p}^{b_0\%p} (mod\ p)\\ C_{a/p}^{b/p} \equiv C_{a^{k}}^{b^{k}}C_{a^{k-1}}^{b^{k-1}}...C_{a^{1}}^{b^{1}} (mod\ p)\\ C_a^b \equiv C_{a/p}^{b/p}*C_{a\%p}^{b\%p} (mod\ p) \]
因为\(1<=p<=1e6\),我们对于每个\(C_{a\%p}^{b\%p}\)可以利用阶乘和阶乘的逆元求出,复杂度为\(O(plogp)\)
int qpow(int a, int b, int p)
{
int res = 1;
while (b)
{
if (b & 1)
res = res * a % p;
b >>= 1;
a = a * a % p;
}
return res % p;
}
int C(int a, int b, int p)
{
int res = 1;
for (int i = 1, j = a; i <= b; ++i, --j)
{
res = res * j % p;
res = res * qpow(i, p - 2, p) % p;
}
return res % p;
}
int lucas(int a, int b, int p)
{
if (a < p && b < p)
return C(a, b, p);
return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
不取模求组合数
\[C_a^b=\frac{a!}{b!(a-b)!} \]我们可以将\(C_a^b\)的质因子分解出来,然后利用高精度乘法运算
那么对于质因子\(p\)来说,它在\(C_a^b\)中的幂次为:\(a!\)中\(p\)的幂次减去\(b!\)和\((a-b)!\)中\(p\)的幂次,所以本质上我们需要对阶乘分解质因数,所以我们可以先利用线性筛求出\([2,a]\)所有的质数,然后分别对每个质数\(p\)求出在\(a!,b!,(a-b)!\)
的幂次,最后我们只要运用高精度乘法即可解决,这样就避免了使用高精度除法
int p[N], vis[N], idx;
int cnt[N];
vector<int> mul(vector<int> &a, int b)
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size() || t; ++i)
{
if (i < a.size())
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (c.size() > 1 && c.back() == 0)
c.pop_back();
return c;
}
void get_primes(int n)
{
for (int i = 2; i <= n; ++i)
{
if (!vis[i])
p[++idx] = i;
for (int j = 1; j <= idx && p[j] * i <= n; ++j)
{
vis[p[j] * i] = 1;
if (i % p[j] == 0)
break;
}
}
}
int get_fact(int n, int p)
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
void solve()
{
int a, b;
cin >> a >> b;
get_primes(a);
for (int i = 1; i <= idx; ++i)
{
cnt[p[i]] = get_fact(a, p[i]) - get_fact(b, p[i]) - get_fact(a - b, p[i]);
}
vector<int> ans;
ans.push_back(1);
for (int i = 1; i <= idx; ++i)
{
for (int j = 1; j <= cnt[p[i]]; ++j)
ans = mul(ans, p[i]);
}
for (int i = ans.size() - 1; i >= 0; i--)
cout << ans[i];
}
卡特兰数
我们借用题目引入卡特兰数:
给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\),它们将按照某种顺序排成长度为 \(2n\) 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列有多少个。
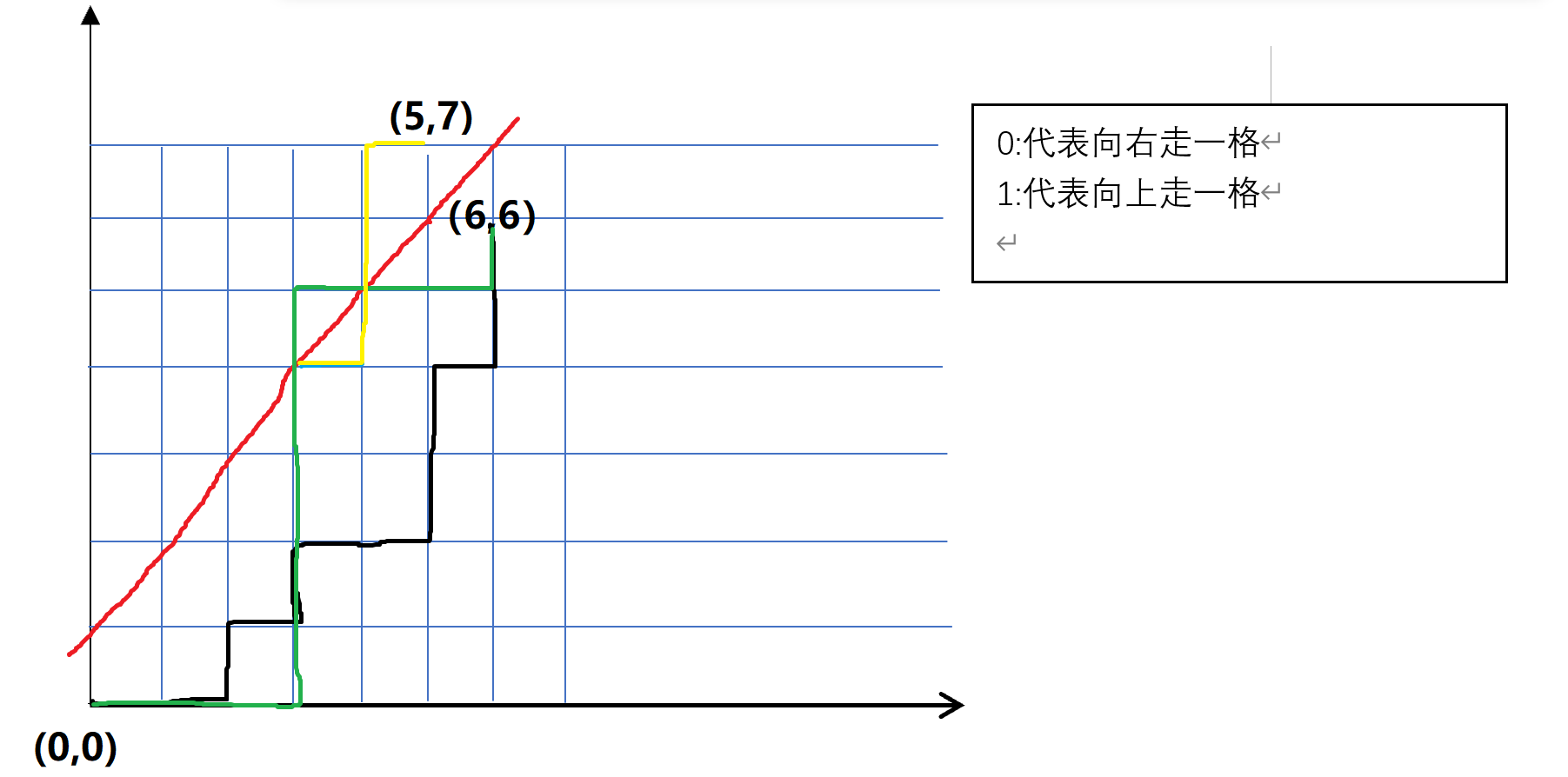
我们将题目转化到二维平面上,设\(0\):向右走一格,\(1\):向上走一格,\(n=6\),我们得到直角坐标系:
我们发现每一条路径都对应且唯一对应一个\(01\)序列,如果\(01\)序列合法,那儿我们的路径一定不能经过图中红色的直线,我们知道从\((0,0)\)到\((6,6)\)的路径方案数为\(C_{12}^6\),我们需要减去经过红色直线的路径数即可得到不经过红色直线的路径数量,我们对于任意一条经过红色直线的路径在其第一个到达红色直线的点往后以红色直线为轴,做轴对称,发现经过红色直线的路径终点一定是\((5,7)\),即经过红色直线的路径数为\(C_{12}^5\),所以最终合法的路径数量为\(C_{12}^6-C_{12}^5\)
所以我们得到结论,能够满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列的个数为:
\[C_{2n}^{n}-C_{2n}^{n-1}=\frac{C_{2n}^{n}}{n+1} \]这就是卡特兰数。
卡特兰数的应用很广泛,尤其是\(01\)序列,括号序列
容斥原理 \(O(2^n)\)
\[|s_1\bigcup s_2 \bigcup s_3 \bigcup ... \bigcup s_n|=\\ |s_1|+|s_2|+...+|s_n|\\ -|s_1\bigcap s_2|- |s_1\bigcap s_3|-...-|s_{n-1}\bigcap s_n|\\ +|s_1\bigcap s_2 \bigcap s_3|- |s_1\bigcap s_3 \bigcap s_4|-...-|s_{n-2}\bigcap s_{n-1}\bigcap s_n|\\ -...-\\ +...+ \]我们推导可得:如果选择的是奇数个集合的交集,那么应该加上交集中的元素个数,如果选择的是偶数个集合的交集,那么应该减去交集中的元素个数
我们分析一下容斥原理的时间复杂度:
\[C_n^0+C_n^1+C_n^2+...+C_n^n=2^n\\ C_n^1+C_n^2+...+C_n^n=2^n - 1 \]很明显,一共有\(2^n-1\)项,所以时间复杂度为\(2^n\)
那么我们对它的所有项进行枚举的时候可以利用二进制进行枚举,也可以利用\(dfs\)搜索进行枚举
下面看一道例题:
给定一个整数 \(n\) 和 \(m\) 个不同的质数 \(p_1,p_2,…,p_m\)
请你求出 \(1∼n\) 中能被 \(p_1,p_2,…,p_m\) 中的至少一个数整除的整数有多少个
\(1<=m<=16\)
\(1<=n,p_i<=10^9\)
题解:容斥原理 + 二进制枚举 \(O(2^mm)\)
设\(|s_p|\)为\([1,n]\)中被\(p\)整除的整数个数,那么答案为\(|s_{p_1}\bigcup s_{p_2} \bigcup s_{p_3} \bigcup ... \bigcup s_{p_m}|\),显然可以运用容斥原理求解,但是我们首先需要知道每个交集中元素的个数:
对于\(|s_{p_1}|\)来说,该集合中元素个数为 : \(\lfloor \frac{n}{p_1} \rfloor\)
对于 \(|s_{p_1} \bigcap s_{p_2}|\)来说,代表既能被\(p_1\)整除和被\(p_3\)的集合两个集合的交集中的元素个数,因为\(p_1\)和\(p_2\)互质,所以交集中元素个数为\(\lfloor \frac{n}{p_1p_2} \rfloor\)
同理,对于\(|s_{p_1} \bigcap s_{p_2} ... \bigcap s_{p_k}|\)来说,因为\(p_i\)为质数,所以这些集合的交集中的元素个数为\(\lfloor \frac{n}{p_1p_2...p_k} \rfloor\)
那么知道了每个集合中元素的个数,我们需要知道如何枚举:
我们可以利用二进制进行枚举,枚举\([1,2^m-1]\),二进制上1代表选择该集合,0代表不选择该集合,如果我们选择的集合数为偶数,答案需要减去这部分贡献,如果是奇数,我们需要加上这部分贡献
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e5 + 10, M = 4e5 + 10;
int n, m;
int p[N];
void solve()
{
cin >> n >> m;
for (int i = 0; i < m; ++i)
cin >> p[i];
int ans = 0;
for (int i = 1; i < (1 << m); ++i)
{
int t = 1;
int cnt = 0; // 选择了几个集合,即二进制中有几个1
for (int j = 0; j < m; ++j)
{
if (i >> j & 1)
{
cnt++;
t *= p[j];
}
if (t > n)
break;
}
if (cnt % 2)
ans += n / t;
else
ans -= n / t;
}
cout << ans << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
博弈论
公平组合游戏\(ICG\)
若一个游戏满足:
- 由两名玩家交替行动
- 在游戏进程的任意时刻,每名玩家执行的操作性质相同
- 不能行动的玩家判负
则该游戏被称为一个公平组合游戏
\(NIM\)游戏
\(NIM\)游戏就是一个公平组合游戏
必胜状态:可以走到某一个必败状态,即留给对手的是一个必败状态
必输状态:走不到任何一个必败状态,即留给对手的只有必胜状态
例题一
给定 \(n\) 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),每堆石子的数量为\(a_i\),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜
结论:\(a_1\bigoplus a_2 \bigoplus ...a_n=0\),先手必输,否则先手必赢
证明:首先我们知道必败状态为:\(0\bigoplus 0 \bigoplus ...0=0\)
- 那么我们只要证明在\(a_1\bigoplus a_2 \bigoplus ...a_n \neq0\)时,先手可以通过拿走一定数量的石子,使得\(a_1\bigoplus a_2 \bigoplus ...a_n=0\),即将先手一定能将必输状态抛给对手:
我们设\(a_1\bigoplus a_2 \bigoplus ...a_n = x\),设\(x\)二进制最高位1在第\(k\)位,显然一定存在\(a_i\),其二进制第\(k\)位
一定是1,显然我们又知道\(a_i \bigoplus x < a_i\),所以我们不妨令\(a_i:=a_i \bigoplus x\),那么这样一定存在\(a_1\bigoplus a_2 \bigoplus ...\bigoplus a_i \bigoplus x...a_n = x \bigoplus x = 0\),所以先手一定能通过拿走一定数量的石子将
必输状态抛给对手
- 那么我们还要证明 在\(a_1\bigoplus a_2 \bigoplus ...a_n=0\)时,先手可以通过拿走一定数量的石子,一定会
使得\(a_1\bigoplus a_2 \bigoplus ...a_n\neq0\),即无法抛给对手一个必输的状态,那么现在先手一定必输
我们利用反证法证明:
假设存在先手在第\(i\)堆石子中通过拿走一定数量的石子使得\(a_1\bigoplus a_2 \bigoplus ...\bigoplus a_i'...a_n = 0\),
那么我们一定可以得到\(a_i=a_i'\),与题目矛盾,我们无论如何都无法使得\(a_i=a_i'\)
例题二:台阶-\(NIM\)游戏
现在,有一个 \(n\) 级台阶的楼梯,每级台阶上都有若干个石子,其中第 \(i\) 级台阶上有 \(a_i\) 个石子(\(a_i≥1\))。
两位玩家轮流操作,每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中(不能不拿)。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
结论:如果奇数级台阶上的石子数异或和为0,则先手必败,否则先手必胜
证明:
首先我们发现如果所有奇数级台阶上都没有石子,只有偶数级台阶上有石子,那么先手必败,因为我们如果想要将偶数级上的石子拿到地面需要偶数次,显然先手拿的人必败,所以当奇数级台阶上没有石子时是必败态,那么我们可以将奇数级台阶看作是一个经典的\(NIM\)游戏,即当奇数级台阶上石子数量的异或和为0时是必败态
假设现在奇数级台阶上石子数量的异或和不为\(0\),那么根据\(NIM\)游戏,我们总可以通过从某个奇数台阶拿走一部分石子来使得奇数台阶上石子数量异或和为\(0\),也就是将必败态留给对手
轮到后手时,现在局面是奇数台阶上石子数量异或和为0,那么后手有两种选择:
选择在偶数台阶上拿走\(x\)个石子放到下一个台阶上,那么先手可以在下一个台阶上拿走\(x\)个石子,放到下一个偶数台阶上,这样后手依旧遇到必败态
选择在奇数台阶上拿走\(x\)个石子放到下一个台阶上,此时奇数台阶上异或和可能不为0,那么根据\(NIM\)游戏,先手总可以在奇数台阶上拿走一部分石子,使得异或和为0,这样又将必败态留给对手
综上:如果奇数级台阶上石子数量的异或和不为0,后手面对的局面始终是奇数级台阶上异或和为0的情况,即必败态,所以先手必胜
\(Mex\)运算
设\(S\)表示一个非负整数集合,定义\(Mex(S)\)为求出不属于集合\(S\)的最小非负整数的运算
\(SG\)函数
什么是终点局面?终点局面代表没有出边,即如果某个局面到不了其他局面,那么该局面就是终点局面
我们将终点局面的\(SG\)函数定义为\(0\)
\[我们定义SG[x]=Mex \{SG(y_1),SG(y_2),...,SG(y_k) \} \]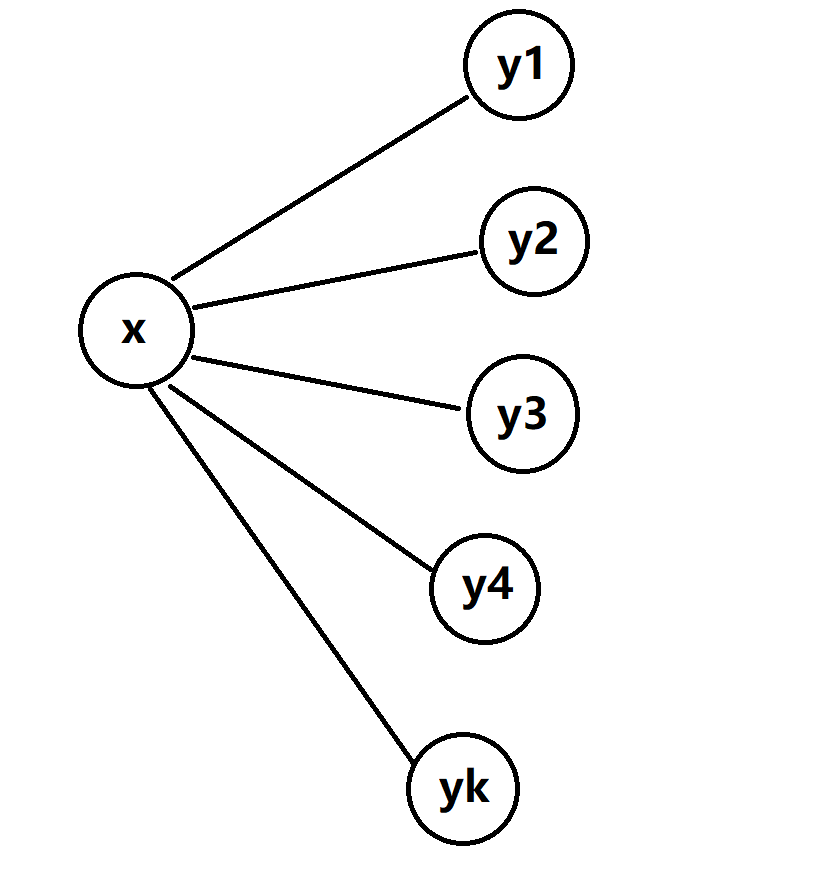
如果\(SG(x) \neq0\),而终点局面的\(SG\)函数为\(0\),说明我们存在走到\(0\)的边,也就是说我们可以走到一个必败状态,即对手永远会遇到必败状态,所以当\(SG(x) \neq 0\),先手必胜
如果\(SG(x)=0\),先手已经是\(0\)的局面了,只能走到\(SG\)非\(0\)的局面,也就是说走不到任何必败状态,然而对手绝顶聪明,每次都会将必败状态抛给先手,即先手每次遇到的局面为\(0\),所以先手必败
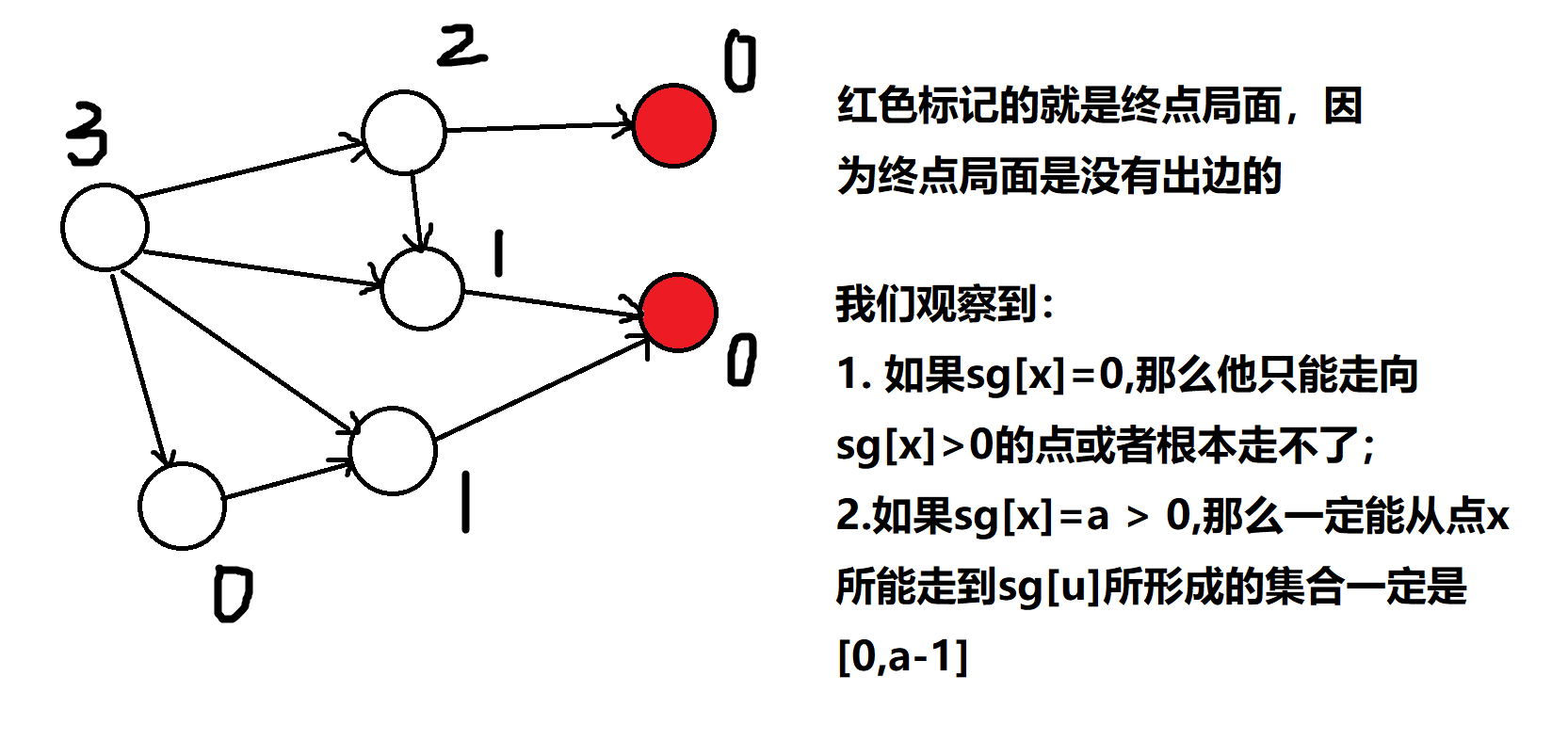
但是如果说有多张有向图的话,怎么解决?
\(SG\)定理:
若\(SG[x_1] \bigoplus SG[x_2] \bigoplus SG[x_3] ... \bigoplus SG[x_k]=0\),则先手必败,否则先手必胜
- \(SG(x_1,x_2,...,x_k)=SG[x_1] \bigoplus SG[x_2] \bigoplus SG[x_3] ... \bigoplus SG[x_k]\)
证明:类似\(NIM\)游戏,不再赘述
同时我们发现\(NIM\)游戏结论可以通过\(SG\)函数得到
例题一:集合-\(NIM\)游戏
给定 \(n\) 堆石子以及一个由 \(k\) 个不同正整数构成的数字集合 \(S\)。
现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合 \(S\),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜
\(1≤n,k≤100\)
\(1≤s_i,h_i≤10000\)样例:
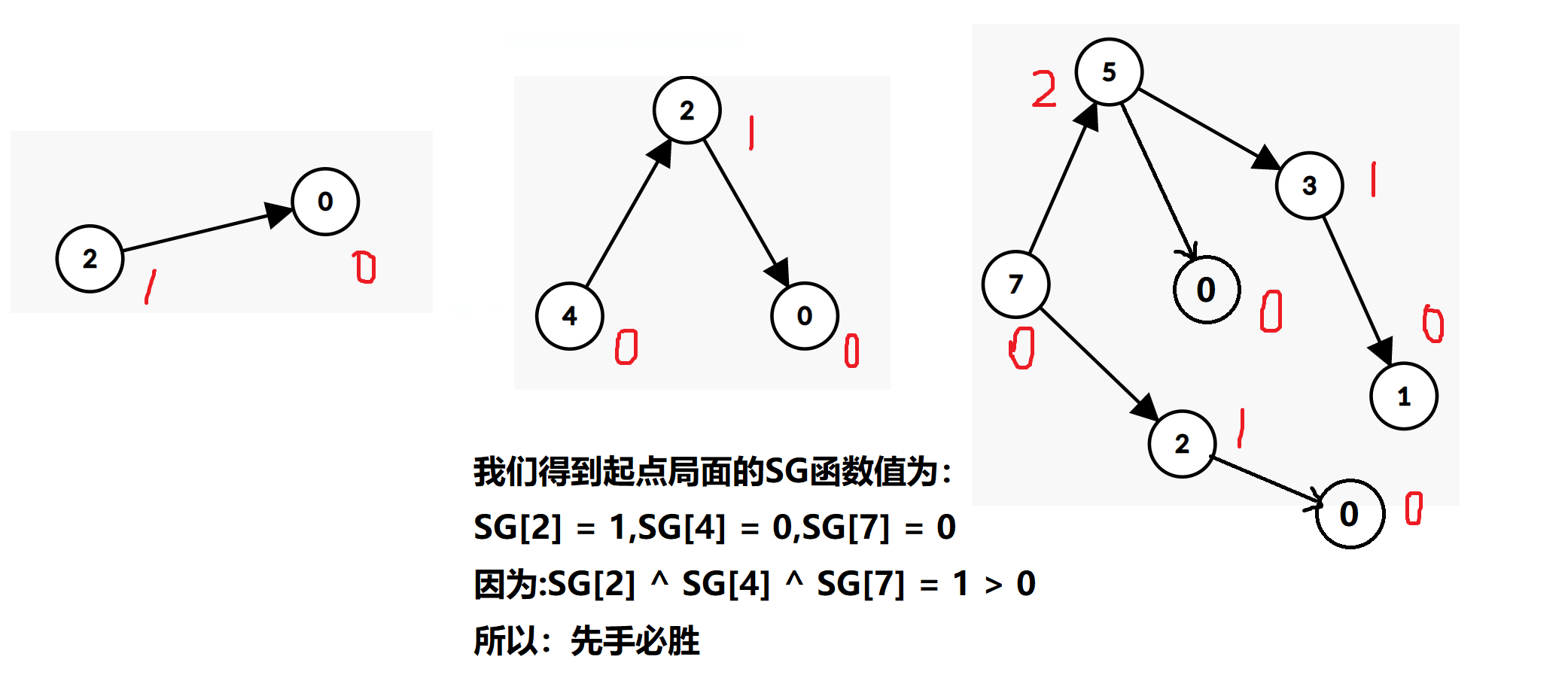
2 2 5 3 2 4 7
我们可以得到\(3\)张有向图以及其\(SG\)函数:
那么如何在利用程序实现?
显然我们发现每一张有向图是一颗树,借助树形\(dp\)的思想,我们可以利用哈希表存储节点\(u\)的所有子节点的\(sg\)函数值,然后在回溯时根据\(Mex\)运算暴力求出节点\(u\)的\(sg\)函数值,所以遍历每一张图的时间为\(O(hk)=1e6\),但是我们如果遍历所有图一定会超时,时间复杂度为\(O(nhk)=1e8\),所以我们需要记忆化搜索使得复杂度退化为\(O(hk)=1e6\)
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e4 + 10, M = 4e5 + 10;
int n, k;
int f[N], s[N];
int sg(int x)
{
if (f[x] != -1) // 记忆化
return f[x];
unordered_map<int, int> mp;
for (int i = 1; i <= k; ++i) // 将所有可达子节点的sg值加入哈希表
{
if (x >= s[i])
mp[sg(x - s[i])]++;
}
for (int i = 0;; i++) // 暴力进行Mex运算
if (!mp[i])
return f[x] = i;
}
void solve()
{
cin >> k;
memset(f, -1, sizeof f);
for (int i = 1; i <= k; ++i)
cin >> s[i];
int ans = 0;
cin >> n;
for (int i = 1; i <= n; ++i)
{
int x;
cin >> x;
ans ^= sg(x);
}
if (ans > 0)
cout << "Yes" << endl;
else
cout << "No" << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
例题二:拆分-\(NIM\)游戏
给定 \(n\) 堆石子,两位玩家轮流操作,每次操作可以取走其中的一堆石子,然后放入两堆规模更小的石子(新堆规模可以为 \(0\),且两个新堆的石子总数可以大于取走的那堆石子数),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
样例:
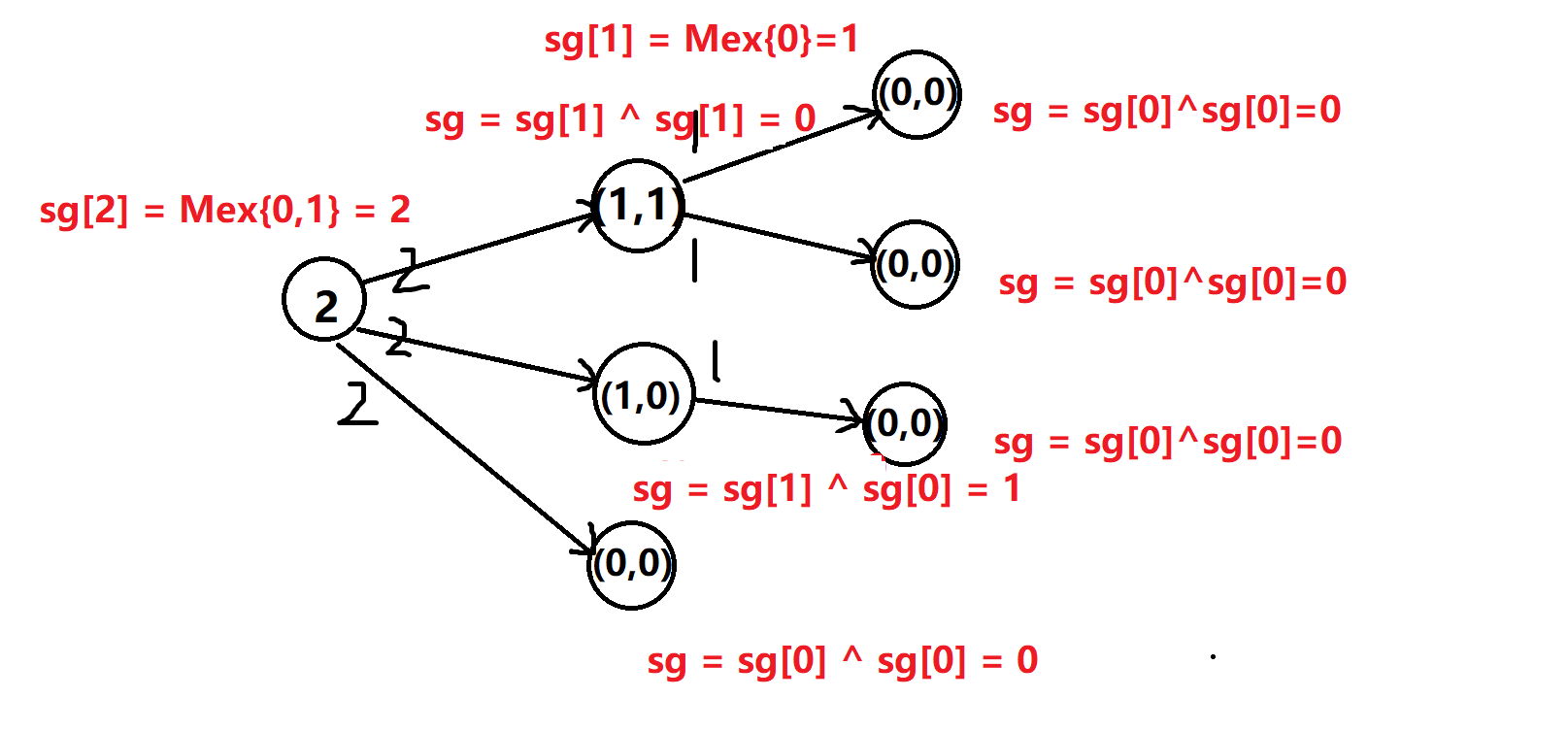
2 2 3
首先我们考虑游戏是否可以结束;我们发现每次操作都有可能会使得石子中的最大数量下降,所以我们发现石子数量的最大值随着游戏回合而减小直到为\(0\),所以该游戏一定能够结束
我们观察样例得到的有向图:
由于一堆石子\(x\)会变成两堆较小的石子\(y_1,y_2\),那么我们根据\(SG\)定理可知,两堆石子的\(SG\)值为\(sg[y_1] \bigoplus sg[y_2]\)
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 1e2 + 10, M = 4e5 + 10;
int n;
int f[N];
int sg(int x)
{
if (f[x] != -1)
return f[x];
unordered_map<int, int> mp;
for (int i = 0; i < x; ++i)
for (int j = 0; j <= i; ++j)
mp[sg(i) ^ sg(j)]++;
for (int i = 0;; i++)
if (!mp.count(i))
return f[x] = i;
}
void solve()
{
memset(f, -1, sizeof f);
cin >> n;
int ans = 0;
for (int i = 1; i <= n; ++i)
{
int x;
cin >> x;
ans ^= sg(x);
}
if (ans)
cout << "Yes" << endl;
else
cout << "No" << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
数论分块(整数分块)\(O(\sqrt{n})\)
知识点定位:在数论问题中解决一些问题的前置知识和基础技巧
问题定义:给定正整数\(n\),求\(\sum_{i=1}^{n}\lfloor\frac{n}{i}\rfloor\)
- 寻找规律:模拟打表找规律
假设\(n=20\)
\(i=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\)
\(\lfloor\frac{n}{i}\rfloor=20,10,6,5,4,3,2,2,2,2,1,1,1,1,1,1,1,1,1,1\)
一个很明显的规律就是存在很多个区间(区间长度可能为\(1\)),使得在区间中有连续个\(\lfloor\frac{n}{i}\rfloor\) 数值相同
那么我们只要把每个区间的左端点\(L\)和右端点\(R\)求出,那么这个问题就能得到简化
- 给出结论:
如果一个区间的左端点是\(L\),那么这个区间的右端点为\(\frac{n}{n/L}\)
int sum = 0; for (int l = 1, r; l <= n; l = r + 1) { r = n / (n / l); sum += (r - l + 1) * (n / l); }
- 时间复杂度分析:
枚举有连续个\(\lfloor\frac{n}{i}\rfloor\) 数值相同的区间个数的复杂度为\(O(\sqrt{n})\)