2022GPLT

老板的作息表

检查任意一张时间表，找出其中没写出来的时间段。

输入第一行给出一个正整数 $N$，为作息表上列出的时间段的个数。随后 $N$ 行，每行给出一个时间段，格式为：
hh:mm:ss - hh:mm:ss
其中 hh、mm、ss 分别是两位数表示的小时、分钟、秒。第一个时间是开始时间，第二个是结束时间。题目保证所有时间都在一天之内（即从 $00:00:00$ 到 $23:59:59$）；每个区间间隔至少 1 秒；并且任意两个给出的时间区间最多只在一个端点有重合，没有区间重叠的情况

题解：按字典序排序 / 区间染色

方法一：

我们发现从$00:00:00$ 到 $23:59:59$，所有时间点的字典序在不断变大，也就是说时间点是按照字典序升序排列的，所以我们不妨将所有给定的时间段按照字典序排序，对于区间$seg_i$和$seg_{i+1}$，来说如果$seg_i$的右端点和$seg_{i+1}$的左端点不相等，就说明中间存在时间空段，直接输出即可

但是我们需要注意：很有可能起始时间点不是$00:00:00$ ,并且终止时间不是$23:59:59$,将两种情况特判即可

方法二：

因为一天所有时间点才86400，所以我们可以在线性的时间内对区间染色，然后对未被染色的区间输出即可，一开始用了差分染色，后来始终调整不对端点处的值，最后发现数据范围很小，可以直接暴力染色

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;

int n;
struct node
{
    string l, r;
    bool operator<(const node &t) const
    {
        return l < t.l;
    }
} s[N];

void solve()
{
    cin >> n;
    char c;
    for (int i = 1; i <= n; ++i)
        cin >> s[i].l >> c >> s[i].r;
    sort(s + 1, s + n + 1);
    string st = "00:00:00";
    string ed = "23:59:59";
    if (s[1].l != st)
        cout << st << " - " << s[1].l << endl;
    for (int i = 2; i <= n; ++i)
    {
        if (s[i].l != s[i - 1].r)
            cout << s[i - 1].r << " - " << s[i].l << endl;
    }
    if (s[n].r != ed)
        cout << s[n].r << " - " << ed << endl;
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

大众情人

有$n$个人，每个人之间存在关系且是有向的，每个人之间的距离感为所有距离中的最小距离；一个人的异性缘是由他/她距离感最远的那个异性决定的，我们定义其异性缘为$\frac{1}{dis_{max}}$,那么大众情人就是异性缘最大的一个人，请你求出两个性别中的大众情人

$1<=n<=500$

题解：$floyd$

看到数据范围果断$floyd$，我们先利用$floyd$求出每个人之间的距离感，然后分别对每一个男性和女性求出其异性缘，然后找到男性和女性中最大的异性缘后，遍历即可得到所有大众情人

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 5e2 + 10, M = 4e5 + 10;

int n;
int f[N][N];
int maxx1[N], maxx2[N];
map<int, bool> mp; // gender

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
        {
            f[i][j] = INF;
            f[i][i] = 0;
            maxx1[i] = -INF;
            maxx2[i] = -INF;
        }
    for (int i = 1; i <= n; ++i)
    {
        char c;
        int k;
        cin >> c >> k;
        if (c == 'F')
            mp[i] = false;
        else
            mp[i] = true;
        for (int j = 1; j <= k; ++j)
        {
            int id, dis;
            cin >> id >> c >> dis;
            f[i][id] = min(f[i][id], dis);
        }
    }
    for (int k = 1; k <= n; ++k)
        for (int u = 1; u <= n; ++u)
            for (int v = 1; v <= n; ++v)
                f[u][v] = min(f[u][v], f[u][k] + f[k][v]);
    int min1 = INF, min2 = INF;
    for (int i = 1; i <= n; ++i)
    {
        if (mp[i] == true)
        {
            for (int j = 1; j <= n; ++j)
            {
                if (mp[j] == false)
                    maxx1[i] = max(maxx1[i], f[j][i]);
            }
            min1 = min(min1, maxx1[i]);
        }
        else
        {
            for (int j = 1; j <= n; ++j)
            {
                if (mp[j] == true)
                    maxx2[i] = max(maxx2[i], f[j][i]);
            }
            min2 = min(min2, maxx2[i]);
        }
    }

    vector<int> ans1, ans2;
    for (int i = 1; i <= n; ++i)
    {
        if (mp[i] == false)
        {
            for (int j = 1; j <= n; ++j)
            {
                if (mp[j] == true && maxx2[i] == min2)
                {
                    ans1.push_back(i);
                    break;
                }
            }
        }
        else
        {
            for (int j = 1; j <= n; ++j)
            {
                if (mp[j] == false && maxx1[i] == min1)
                {
                    ans2.push_back(i);
                    break;
                }
            }
        }
    }
    for (int i = 0; i < ans1.size(); ++i)
        cout << ans1[i] << "\n "[i < ans1.size() - 1];
    for (int i = 0; i < ans2.size(); ++i)
        cout << ans2[i] << "\n "[i < ans2.size() - 1];
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

龙龙送外卖

给定一棵树，有$q$次询问，每次询问时会新增一个标记点，每次询问让你求出从起点开始遍历完所有被标记的点的最短距离是多少，注意我们可以停在最后一个遍历到的标记点上

题解：记忆化 + 树的遍历 + 思维

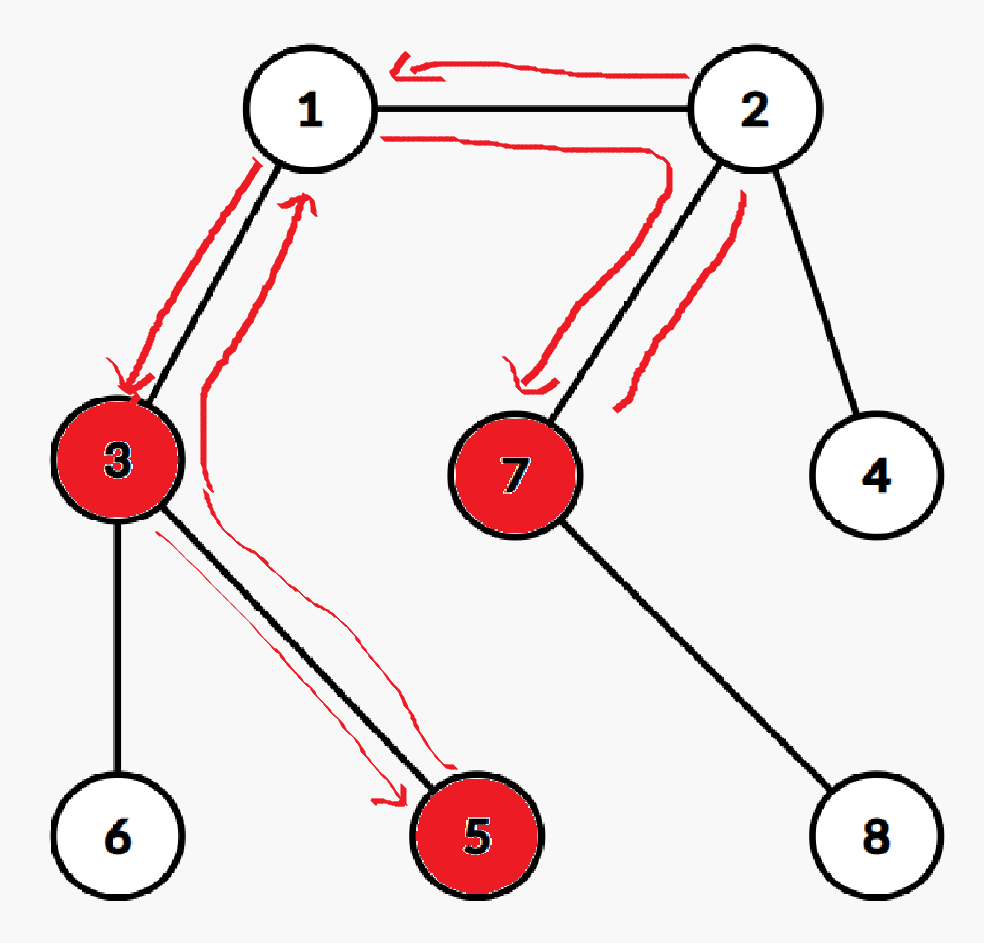
我们假设我们每次遍历完所有标记点后都返回根节点，这样我们很容易发现只要我是选择最短路径去遍历每个点，我们会发现所有被遍历到的边我们都走了两次，设所有被遍历到的边数为$s$；
那么我们再考虑遍历到最后一个标记点后不返回根节点，设最后一个被遍历到标记点的深度为$dep$，那么最后我们走的距离为：$2 * s - dep$,那么我们发现$s$一定是不变的，所以我们为了让距离最短，我们必须使得 $dep$最大，也就是说我们贪心的让深度最大的标记点作为最后一个被被遍历的点即可，答案即为: $2 * s - dep_{max}$

我们考虑如何动态维护边数$s$和最大深度$dep$：

对于最大深度来说，我们可以提前遍历一遍树，预处理求出所有点的深度，然后每次新增标记点的时候取$max$即可

对于边数来说，我们发现对于新增点来说，我们都可以暴力往上跳，边跳边标记，直到遇到之前被遍历过的点，我们停止，那么对于该新增点来说新加的边数就是我标记的数量，可以发现，利用这样记忆化的思想，所有点最多只会被遍历一次，复杂度$O(n)$

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;

int n, m;
int dep[N];
int fa[N];
int vis[N];
vector<int> g[N];

void dfs(int u, int par)
{
    dep[u] = dep[par] + 1;
    for (auto v : g[u])
    {
        if (v == par)
            continue;
        dfs(v, u);
    }
}

void solve()
{
    cin >> n >> m;
    int rt;
    for (int i = 1, u; i <= n; ++i)
    {
        cin >> u;
        if (u == -1)
        {
            rt = i;
            fa[i] = -1;
            continue;
        }
        g[u].push_back(i);
        g[i].push_back(u);
        fa[i] = u;
    }
    dfs(rt, 0);
    int max_dep = -INF;
    int ans = 0;
    for (int i = 1, u; i <= m; ++i)
    {
        cin >> u;
        max_dep = max(max_dep, dep[u] - 1);
        while (!vis[u] && fa[u] != -1)
        {
            vis[u] = 1;
            ans += 2;
            u = fa[u];
        }
        cout << ans - max_dep << endl;
    }
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

关于深度优先搜索和逆序对的题应该不会很难吧这件事

给定一颗$n$个节点的树，其中节点$r$为根，求该树所有可能的$dfs$序中逆序对的数量之和，答案对$1e9+7$取模

题解：树状数组求逆序对 + 组合计数

我们发现对于存在祖先关系的节点来说他们互相之间的顺序是固定的，但是对于子节点来说却是自由的不受约束的，设$dfs$序的数量为$sum$，所以我们可以知道$sum$为所有节点的子节点个数的阶乘的乘积，即$\prod cnt[u]!$,$cnt[u]$代表$u$节点的子节点的数量

因为对于存在祖先关系的节点来说他们互相之间的顺序是固定的，所以他们之间的逆序对的数量是固定的，设存在祖先关系的节点之间逆序对的数量为$s_1$,那么存在祖先关系的节点对答案的贡献为$s_1\times sum$，对于$s_1$，我们可以在树上维护树状数组，利用树状数组计算出一条路径上有多少节点比当前节点大，我们只要在递归时加入，回溯时删除即可完成维护

对于不存在祖先关系的节点来说，他们的顺序是任意的，我们来看个例子：

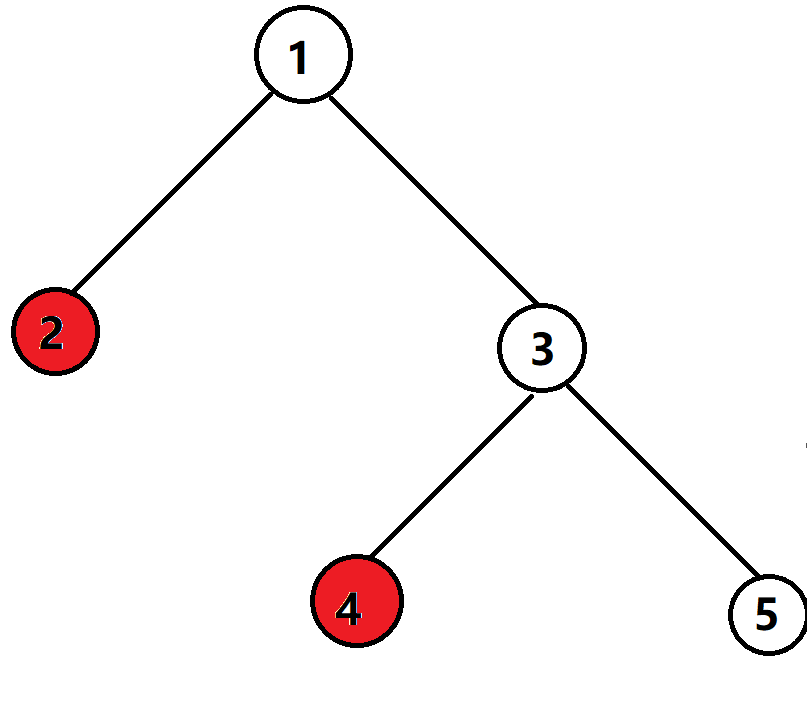
对于节点2和节点4来说，他们之间不存在祖先关系，如果点2要在4的前面，我们就要保证点2在点3的前面遍历，反之如果我们要点4在点2的前面，我们就要保证点3在点2的前面遍历，所以说我们观察得到任意一对不存在祖先关系的节点，他们构成逆序对的数量为$\frac{sum}{2}$，也就是说在一半数量的$dfs$序中节点4都会在节点2前面且形成逆序对;

所以我们对于每个节点u，我们找到其所有不存在祖先关系的节点数$num[u]$，令$s_2=\sum num[u]$,那么不存在祖先关系的节点对答案的贡献$s_2\times \frac{sum}{2} \times \frac{1}{2} $,为什么还要乘以$\frac{1}{2}$呢？因为我们在计算节点4的不存在祖先关系的贡献时将2加入贡献，但是在对2计算贡献时把4也加入了，也就是说贡献重复计算了

那么我们如何计算对于一个点u来说，与u不存在祖先节点的节点数量呢？

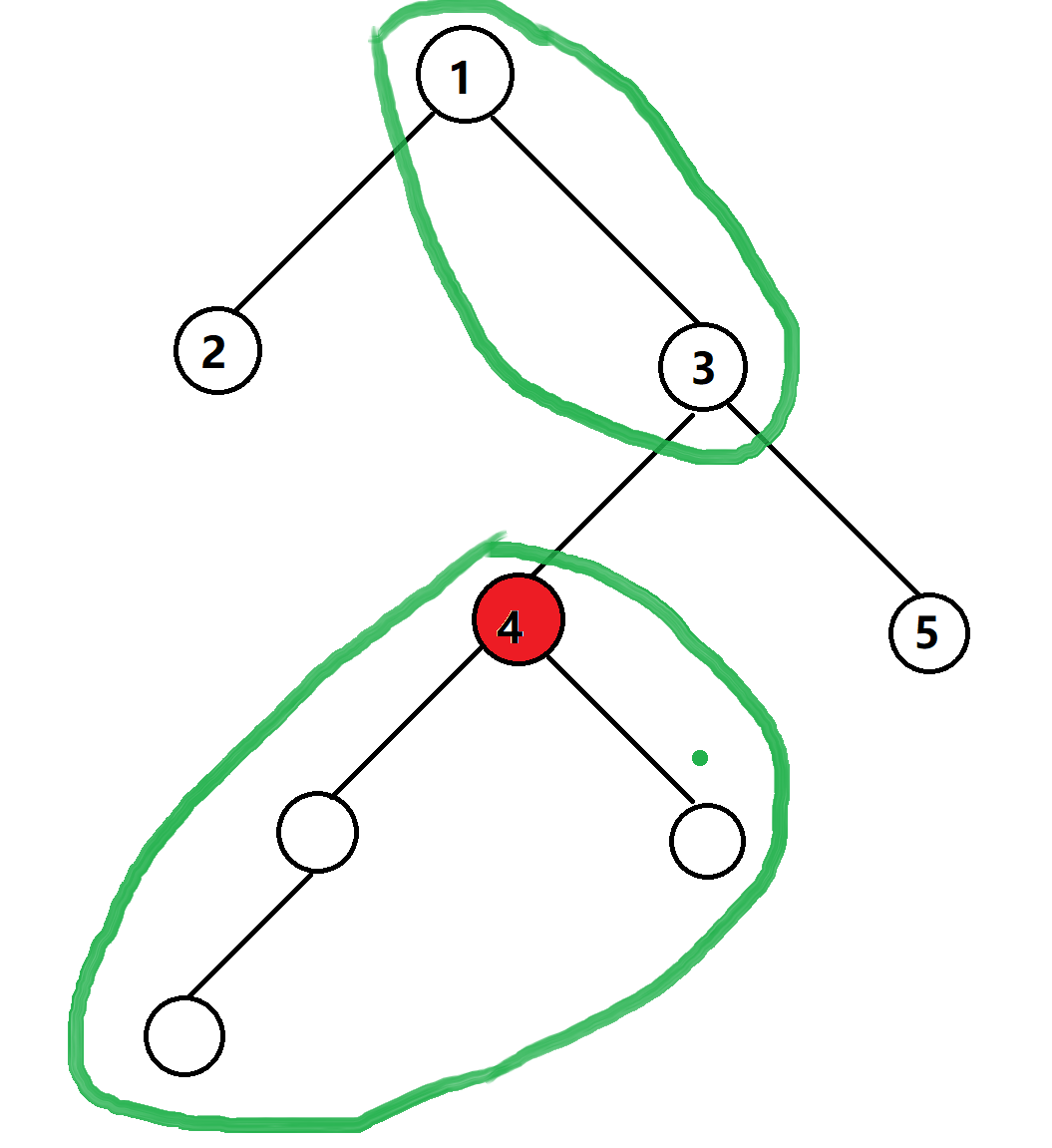
我们发现与u不存在祖先关系的节点数量为，所有节点数n减去节点u的子树大小再减去和节点4存在祖先关系的节点数, 即$num[u]=n-sz[u]-cnt$,设$cnt$为与节点u存在祖先关系的节点数

#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 3e5 + 10, M = 4e5 + 10;

int n, rt;
vector<int> g[N];
int s1, s2;
int sum = 1;
int sz[N];
int c[N];

int qpow(int a, int b, int p)
{
    int res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % p;
        b >>= 1;
        a = a * a % p;
    }
    return res % p;
}

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int v)
{
    while (x <= n)
    {
        c[x] += v;
        x += lowbit(x);
    }
}

int get_sum(int x)
{
    int res = 0;
    while (x > 0)
    {
        res += c[x];
        x -= lowbit(x);
    }
    return res;
}

void dfs(int u, int par)
{
    add(u, 1);
    s1 = (s1 % mod + (get_sum(n) - get_sum(u)) % mod) % mod;
    int cnt = 0; // u节点的子节点个数
    sz[u] = 1;
    for (auto v : g[u])
    {
        if (v == par)
            continue;
        dfs(v, u);
        sz[u] += sz[v];
        cnt++;
    }
    for (int i = 2; i <= cnt; ++i)
        sum = (sum % mod * i % mod) % mod;
    add(u, -1);
    s2 = (s2 % mod + (n - sz[u] - get_sum(n)) % mod) % mod;
}

void solve()
{
    cin >> n >> rt;
    for (int i = 1, u, v; i < n; ++i)
    {
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(rt, 0);
    int ans = ((s1 % mod * sum % mod) % mod + ((s2 % mod * sum % mod * qpow(4, mod - 2, mod) % mod) % mod)) % mod;
    cout << ans << endl;
}
signed main(void)
{
    Zeoy;
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

posted @ 2023-04-10 18:10 Zeoy_kkk 阅读(30) 评论(0) 编辑收藏举报

刷新页面返回顶部

Zeoy-kkk

2022GPLT

老板的作息表

题解：按字典序排序 / 区间染色

大众情人

题解：\(floyd\)

龙龙送外卖

题解：记忆化 + 树的遍历 + 思维

关于深度优先搜索和逆序对的题应该不会很难吧这件事

题解：树状数组求逆序对 + 组合计数

公告