Educational Codeforces Round 77 (Rated for Div2)
B - Obtain Two Zeroes
给定两个整数\(a,b\),你可以执行以下操作任意次:每次操作选择一个正整数\(x\),使得\(a:=a-x,b:=b-2x\)或者\(a:=a-2x,b:=b-x\),问你是否能通过操作使得\(a,b\)都为同时为\(0\)
题解:思维
假设\(a<b\)
- 我们可以得到\(a-x+b-2x=0\)==>\(a+b=3x\),显然我们可以得到如果我们能通过操作使得\(a,b\)同时为\(0\),我们可以得到$3\ |\ (a+b) $
- 但是一定存在限制条件,比如说\(a=1,b=8\)时,就无法同时变为\(0\),我们不妨令\(x=1\),我们发现\(a-=1,b-=2\)会使得\(b\)和a之间的差距缩小\(1\),如果在\(a\)变为\(0\)之前\(b\)还没有追上\(a\),那一定无法同时为\(0\),当时的情况一定是\(a=0,b>0\),如果在\(a\)变为\(0\)之前\(b\)已经追上了\(a\),我们经过模拟之后发现,\(a\)和\(b\)之间只要交替\(-1\),\(-2\)就能实现同时为\(0\),所以我们只要判断在\(a\)变为\(0\)之前\(b\)有没有追上\(a\)即可
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
void solve()
{
int a, b;
cin >> a >> b;
if (a > b)
swap(a, b);
if ((a + b) % 3 == 0)
{
int k = b - a;
if (a - k < 0 || b - 2 * k < 0)
{
cout << "NO" << endl;
}
else
cout << "YES" << endl;
}
else
cout << "NO" << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
cin >> T;
while (T--)
{
solve();
}
return 0;
}
C - Infinite Fence
给你无限多的木板,木板的下标从\(1\)到无穷大,你需要在木板上填涂颜色,给定正整数\(r,b\),给出填涂颜色的规则:
- 如果该木板的下标能够整除\(r\),则涂成红色;
- 如果该木板的下标能够整除\(b\),则涂成蓝色;
- 如果同时整除\(r,b\),则你可以任意选择其中一种颜色填涂
- 如果都不整除,你不能涂颜色
最后将涂色的木板抽出,按照下标从小到大排序,如果存在超过连续的\(k\)个相同颜色的木板,就代表涂色不合法,输出"REBEL", 否则输出"OBEY"
题解:思维 + 循环节 + 裴蜀定理 : 好题目
假设\(r<b\):
- 首先我们知道在\(r\)和\(b\)公倍数的位置可以任意选择一种颜色填涂,那么我们需要解决的是在这个位置究竟能不能确定填涂什么颜色?
我们不难发现填涂的颜色构成了循环节,也就是说每个重叠的部分都是循环的开始,我们发现在重叠部分的两边一定是红色,所以我们一定会贪心的将重叠部分涂成蓝色,这样我们就确定了任选颜色的位置实际上就是填涂的颜色已经固定了,也就是\(r\)和\(b\)之间较大的数,在这里也就是蓝色木板
- 其次知道了上面的推论,我们肯定可以确定如果会出现超过连续\(k\)次相同颜色的木板马,那一定是红色木板,那么我们需要找到两个蓝色木板之间最多能涂几个红色木板:
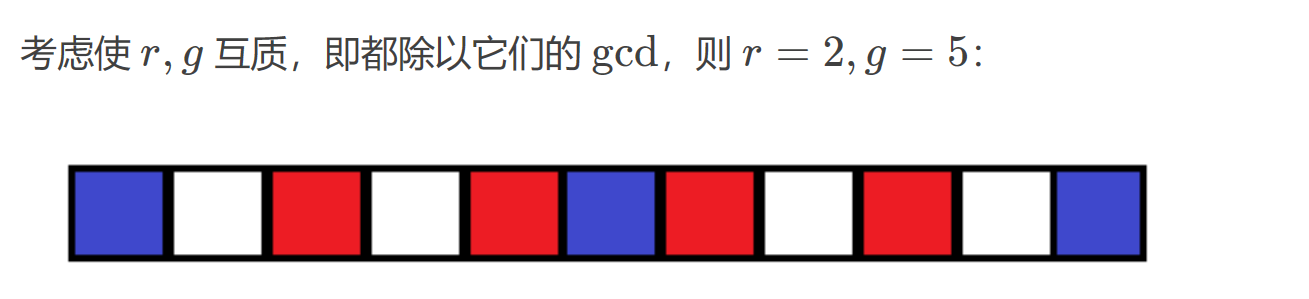
因为木板无限多,所以我们不妨将填涂颜色的位置的下标都除以\(gcd(r,b)\),这样填涂颜色的木板之间的相对位置是不会改变的,即\(r':=r/gcd(r,b),b'=b/gcd(r,b)\),显然我们可以发现现在\(r'\)和\(b'\)互质,由裴蜀定理得,存在正整数\(x,y\)使得\(r'x-b'y=1\)
简单的理解就是一定存在两个位置使得红色木板恰好就在蓝色木板后一个位置,那么此时两个蓝色木板之间能够涂的红色木板数量一定是最多的,数量为\(\lceil \frac{b-1}{r} \rceil\),我们只需要判断这个最大数量和\(k\)的大小进行比较即可
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
void solve()
{
int r, b, k;
cin >> r >> b >> k;
if (r > b)
swap(r, b);
int p = gcd(r, b);
r /= p;
b /= p;
int cnt = (int)ceil(1.0 * (b - 1) / r);
if (cnt >= k)
cout << "REBEL" << endl;
else
cout << "OBEY" << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
cin >> T;
while (T--)
{
solve();
}
return 0;
}
D - A Game with Traps
你有\(m\)个士兵,每个士兵的敏捷度为\(a_i\),现在你要带领一些士兵从线段的\(0\)点到\(n+1\)点,但是线段上有\(k\)个陷阱,每个陷阱范围为\([l_i,r_i]\),且每个陷阱的危险度威威\(d_i\),如果士兵的敏捷度\(a_i<d_i\),那么只要士兵踏入陷阱就会死亡,但是陷阱无法伤害你,每个陷阱\(r_i\)处可以解除陷阱,只有你可以解除陷阱。你可以选择一些士兵,并在规定时间\(t\)秒内带着所有你所选择的士兵(也就是说你所选择的士兵不能死亡,必须全部存活)从\(0\)点到\(n+1\)点,你可以进行以下操作:
- 若你的位置是 \(x\),则可以耗费 \(1\) 秒走到 \(x-1\) 或 \(x+1\)。
- 若你和士兵的位置是 \(x\),则可以耗费 \(1\) 秒走到 \(x-1\) 或 \(x+1\),但不能让士兵处于危险之中。
- 若你的位置是 \(x\),并且满足 \(r_i=x\),你可以解除这个陷阱(不花费时间)。
在操作后,你和小队的坐标都应为整数。
你必须选择尽可能多的士兵,在 \(t\) 秒内把它们从 \(0\) 点带到 \(n+1\) 点。
\(l_i,r_i<=2e5\)
题解:二分答案 + 差分染色 + 贪心 : 好题目
显然我们可以先将士兵的灵敏度按照降序排列,然后二分士兵的灵敏度,重点是我们如何在\(O(n)\)的时间内检查合法性
\(check\)中我们分析一下如何以更优的时间来解除陷阱:
- 首先如果\(a[mid] >= d_i\),那么该陷阱不会对选择的士兵造成影响,所以我们没有必要特意去解除
- 那么对于那些会对士兵造成伤亡的陷阱,情况分为两类:
两段陷阱包含的区间不重合:\([l_i,r_i],[l_j,r_j]且r_i<l_j\)
那么对于这种情况显然更优的选择方法是我们先将士兵带到\(l_i-1\)的地方,然后我去\(r_i\)处拆除陷阱,然后再回去带士兵,然后我们再前进到\(l_j-1\)的位置,然后将我再去拆除\(r_j\)处的陷阱,然后再回去带士兵,所以陷阱区间中的每个点我们实际上走了\(3\)次(拆陷阱-->带士兵-->离开陷阱)
两段陷阱包含的区间有重合部分:\([l_i,r_i],[l_j,r_j]且l_i<l_j,r_i>l_j\)
那么对于这种情况我们需要我们不能再实行上面的方案了,因为即使我拆除了\([l_i,r_i]\)处的陷阱,但是我们再回去带兵不能前进到\(l_j\)处,因为我们还有拆除\(r_j\)处的陷阱,所以更优的选择方案就是对于存在重合区间的多个陷阱,我们考虑直接拆除完所有重合区间中所有的陷阱后再回去带兵前进,那么实际上我们只需要将重叠的区间进行合并后,发现这个合并后的区间中的每个点依旧被走了\(3\)次
根据上面分析我们可以知道我们只需要进行陷阱区间合并后染色的操作,然后如果某点存在陷阱,时间贡献\(+3\),如果没有陷阱,时间贡献\(+1\),最后总时间再和\(t\)进行比较即可判断合法性
- 那么对于区间合并后染色的操作我们可以利用差分实现,也就是说我们可以在\(O(n)\)的时间中进行\(check\)
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10, M = 4e5 + 10;
int m, n, k, t;
int a[N];
struct node
{
int l, r, d;
} p[N];
bool check(int mid)
{
int res = 0;
vector<int> dif(n + 10, 0);
for (int i = 1; i <= k; ++i)
{
int l = p[i].l, r = p[i].r, d = p[i].d;
if (d <= a[mid])
continue;
dif[l]++;
dif[r + 1]--;
}
for (int i = 1; i <= n + 1; ++i)
dif[i] = dif[i - 1] + dif[i];
for (int i = 1; i <= n + 1; ++i)
{
if (dif[i] > 0)
res += 3;
else
res++;
}
return res <= t;
}
void solve()
{
cin >> m >> n >> k >> t;
for (int i = 1; i <= m; ++i)
cin >> a[i];
sort(a + 1, a + m + 1, greater<int>());
for (int i = 1; i <= k; ++i)
{
int l, r, d;
cin >> l >> r >> d;
p[i] = {l, r, d};
}
int l = 1, r = m;
while (l <= r)
{
int mid = l + r >> 1;
if (check(mid))
l = mid + 1;
else
r = mid - 1;
}
cout << r << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}
E - Tournament
一场拳击比赛中有\(n\)个人,\(n\)是\(2\)的幂次,其中有一个人是你的朋友,你可以任意安排两两配对进行比赛,这\(n\)个人按照能力大小排列,且能力为\(i\)的人能被贿赂的代价为\(a_i\),如果能力强的人对局能力弱的人,那么能力弱的人就会被淘汰,但是我们可以通过贿赂来使得能力强的故意输掉比赛,如果\(a_i=-1\),则代表这个人是你的朋友,现在你需要帮助你的朋友取得冠军 ,请你求出最少需要花费多少代价使得朋友获得冠军
题解:思维 + 优先队列实现贪心 : 好题目
首先我们通过模拟可以知道,假设现在不贿赂任何人,并且任意安排的对局,我们可以发现:
冠军永远只有\(1\)个,那就是编号为\(n\)的选手
能够进入\(2\)强的人只会出现在\([\frac{n}{2},n]\)中
能够进入\(4\)强的人只会出现在\([\frac{n}{4},n]\)
......
我们知道编号大的人能够存活下来的概率越大,所以我们优先贿赂编号大的人
所以我们得到现在我们的朋友通过安排特定的对局最多能够到达的排名,如果朋友现在处于\([\frac{n}{2},n]\)中,说明我们可以通过安排对局使得朋友成为\(2\)强,最后我们只需要贿赂编号为\(n\)的人(也就是原本的冠军)即可
如果朋友现在处于\([\frac{n}{4},n]\)中,说明我们可以通过安排对局使得朋友成为\(4\)强,但是我需要多贿赂一个人,也就是说我需要贿赂一名本身能够成为\(2\)强的选手让他故意故意输给朋友即可,那么我们只需要在\([\frac{n}{2},n]\)中找一个贿赂代价最小的人贿赂即可,因为这个人的实力本来就可以通过安排对局没有任何花费的使他进入\(2\)强
依次类推,所以我们只需要维护一个区间中的最小值即可,我们考虑利用优先队列实现
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define debug(x) cerr << #x << '=' << x << endl
#define all(x) (x).begin(), (x).end()
#define rson id << 1 | 1
#define lson id << 1
#define int long long
#define mpk make_pair
#define endl '\n'
using namespace std;
typedef unsigned long long ULL;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 3e5 + 10, M = 4e5 + 10;
int n;
int a[N];
priority_queue<int, vector<int>, greater<int>> q;
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
int ans = 0;
for (int i = n; a[i] != -1; --i)
{
q.push(a[i]);
if ((i & (i - 1)) == 0)
{
ans += q.top();
q.pop();
}
}
cout << ans << endl;
}
signed main(void)
{
Zeoy;
int T = 1;
// cin >> T;
while (T--)
{
solve();
}
return 0;
}