POJ - 1797 Heavy Transportation

POJ - 1797 Heavy Transportation

题解：Dij最短路变形

题意：让你求从起点1到起点n的每条路径权重最小值的最大值，显然可以二分答案，但是我们这边考虑利用dij求解。

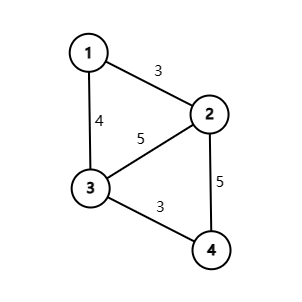
首先来一个样例：

1 2 3

1 3 4

2 3 5

2 4 5

3 4 3

我们会发现题目想要表达的意思就是对于每一条从1到4的路径，我们找出每一条路径中的道路的最小边权，然后对所有路径的最小边权取max,\(w_i\)代表每条路径中的边权

\[max(min(w_i)) \]

实际上我们改变一下dij的松弛条件即可：原来的松弛方程：\(d[v]>d[u]+w\),我们知道每条路径的最小边权实际上就是不断取\(min\)，所以我们可以将松弛方程改为：\(d[v]<min(d[u],w)\),这样就实现了对一条路径每个边权值都取\(min\)，但是我们还需要修改一下细节，首先我们肯定松弛完每条边后我们肯定要选择一个最大的\(d[u]\)去操作，因为这样会使得我们贡献尽可能大，所以我们需要将小根堆改为大根堆，那么\(d[i]\)的初始值也需要改变，那么我们去模拟一下，比如说如果现在所有点还是初始为\(inf\)，那么我们从1到2的时候会出现\(inf<min(0,w)\),明显矛盾，所以我们将所有点距离初始化为0，将起点距离初始化为\(inf\)，那么我们再来看一下从1到2的时候会出现\(0<min(inf,w)\)，显然成立，这样2号点就会被更新了，说明我们找到了正确的初始化。

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#include <sstream>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const double eps = 1e-9;
const int N = 2e5 + 10;
int n, m, flag;
vector<pii> adj[1010];
int dis[1010];
int vis[1010];
void dij(int st)
{
    priority_queue<pii> q;
    q.push(make_pair(inf, st));
    dis[st] = inf;
    while (q.size())
    {
        int u = q.top().second;
        q.pop();
        if (vis[u])
            continue;
        vis[u] = 1;
        for (int i = 0; i < adj[u].size(); ++i)
        {
            int v = adj[u][i].first;
            int w = adj[u][i].second;
            if (dis[v] < min(dis[u], w))
            {
                dis[v] = min(dis[u], w);
                q.push(make_pair(dis[v], v));
            }
        }
    }
}
int main(void)
{
    Zeoy;
    int t = 1;
    cin >> t;
    int cnt = 1;
    while (t--)
    {
        cout << "Scenario #" << cnt++ << ":\n";
        for (int i = 1; i <= n; ++i)
            adj[i].clear(), dis[i] = 0, vis[i] = 0;
        cin >> n >> m;
        for (int i = 1, u, v, w; i <= m; ++i)
        {
            cin >> u >> v >> w;
            adj[u].push_back(make_pair(v, w));
            adj[v].push_back(make_pair(u, w));
        }
        dij(1);
        cout << dis[n] << endl;
        cout << endl;
    }
    return 0;
}