POJ - 3687 Labeling Balls

POJ - 3687 Labeling Balls

题解：反向建边+拓扑排序

先来简单讲一下题意：我们把重量1-N的小球贴上标签，题目给出的输出a->b，就代表贴着标签a的小球必须比贴着标签b的小球轻，最后按照标签1-N输出每个小球的权重，同时如果答案多组，我们要输出权重字典序最小的答案

直接看第一组样例

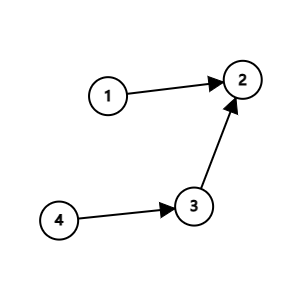
1 2
3 2
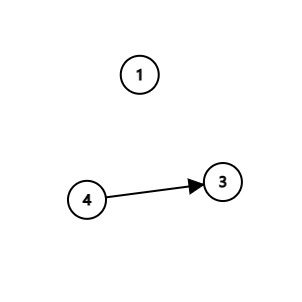
4 3

首先这说明贴着标签2的小球权重最大，也就是最重，所以贴着标签2的小球重量为4；

将连着标签2的球的边去掉后我们发现4一定比3轻，但是3和1谁的权重大不清楚，假设我们把贴着标签1的球的权重设为3，那么标签3的球的权重为2，标签4的球权重为1，所以序列应该是：3 4 2 1

假设我们把贴着标签3的球的权重设为3，那么标签4的球的权重可能是2也可能是1，所以序列应该是：

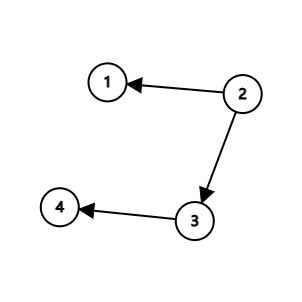
标签4选择1：2 4 3 1或者 标签4选择2：1 4 3 2，很显然1 4 3 2才是我们想要的字典序最小的答案，所以我们发现了什么？我们每次处理的球，是不是它的出度为0，如果说有多个出度为0的球，根据题目要求，我们肯定选择标签最大的球，所以我们可以利用反向建边将出度为0变成入度为0，这样我们只需要去维护一个大根堆的优先队列，实现拓扑排序即可，但是我们要注意，使用拓扑排序要注意题目可能会有自环，在这题中也就是可能会有重边，所以我们需要通过map实现去除重边

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#include <sstream>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
int n, m;
priority_queue<int> q;
map<pii, int> mp;
vector<int> g[210];
int du[210];
int main(void)
{
    Zeoy;
    int t = 1;
    cin >> t;
    while (t--)
    {
        mp.clear();
        cin >> n >> m;
        vector<int> ans(n + 2);
        for (int i = 1; i <= n; ++i)
        {
            g[i].clear();
            du[i] = 0;
        }
        for (int i = 1, u, v; i <= m; ++i)
        {
            cin >> u >> v;
            if (!mp[make_pair(u, v)]) // 去除重边
            {
                g[v].push_back(u);
                du[u]++;
                mp[make_pair(u, v)]++;
            }
        }
        for (int i = 1; i <= n; ++i)
        {
            if (du[i] == 0)
                q.push(i);
        }
        int w = n;
        int num = 0;
        while (q.size())
        {
            int t = q.top();
            num++;
            ans[t] = w--;
            q.pop();
            for (int i = 0; i < g[t].size(); ++i)
            {
                du[g[t][i]]--;
                if (du[g[t][i]] == 0)
                {
                    q.push(g[t][i]);
                }
            }
        }
        if (num < n)						//判断有无自环
            cout << -1 << endl;
        else
        {
            for (int i = 1; i <= n; ++i)
            {
                cout << ans[i] << " ";
            }
            cout << endl;
        }
    }
    return 0;
}