贪心入门
贪心入门
贪心模型一:选择最大的不相交区间
题目一般都是活动安排类,想要参加更多的活动,要求参加的活动时间不能冲突
HDU - 2037
确实如此,世界杯来了,球迷的节日也来了,估计很多ACMer也会抛开电脑,奔向电视了。
作为球迷,一定想看尽量多的完整的比赛,当然,作为新时代的好青年,你一定还会看一些其它的节目,比如新闻联播(永远不要忘记关心国家大事)、非常6+7、超级女生,以及王小丫的《开心辞典》等等,假设你已经知道了所有你喜欢看的电视节目的转播时间表,你会合理安排吗?(目标是能看尽量多的完整节目)
思路:因为想要参加更多的活动,所以我们需要节目时间尽可能结束的早一点,所以按照区间右端点升序排列,第一个活动我们一定会参加,ans=1现在now就是第一个区间的右端点,我们去找第一个区间之后,有没有区间的左端点比now大,如果找到,更新now的值为现在已找到区间的右端点,ans++,重复以上步骤即可。
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
pii a[110];
int cmp(pii x, pii y)
{
return x.second < y.second;
}
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
while (cin >> n, n)
{
for (int i = 1; i <= n; ++i)
{
cin >> a[i].first >> a[i].second;
}
sort(a + 1, a + 1 + n, cmp); //按照区间右端点升序排列
int now = a[1].second; //初始位置
int ans = 1; //不相交区间数量
for (int i = 2; i <= n; ++i)
{
while (i <= n && now > a[i].first) //找到第一个左端点>=now的区间
i++;
if (i <= n)
{
now = a[i].second; //更新now为现在区间右端点
ans++;
}
}
cout << ans << endl;
}
}
return 0;
}
贪心模型二:区间选点问题
典型例题:区间选点
题目描述:数轴上有n个闭区间\([l,r]\),取尽量少的点,使得每个区间都至少有一个点(不同区间内含的点可以是同一个)
思路:因为取尽量少的点,所以我们把点放在端点处能够更好产生价值,但是到底是按左端点排序还是按右端点排序呢,我们来看一个例子[1,8],[2,4],[3,5],[4,9],如果按照左端点升序,我们就会发现如果要使一个点包含更多区间,只能取在一个区间的中间,没有取在端点处,所以不符合我们下的定义,所以我们之直接按照右端点升序排列即可,取第一个端点的右端点为now,ans=1如果后面的区间有区间的左端点比now大,我们直接更新now为找到区间的右端点,ans++,说明我们现在的now这个点包含不住了,只能再加一个点
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
pii a[110];
int cmp(pii x, pii y)
{
return x.second < y.second;
}
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
while (cin >> n, n)
{
for (int i = 1; i <= n; ++i)
{
cin >> a[i].first >> a[i].second;
}
sort(a + 1, a + 1 + n, cmp); //按照区间右端点升序排列
int now = a[1].second; //初始位置
int ans = 1; //选的点的数量
for (int i = 2; i <= n; ++i)
{
if (now<a[i].first) //如果当前区间的左端点比now大,更新now,并增加一个点
{
ans++;
now = a[i].second;
}
}
cout << ans << endl;
}
}
return 0;
}
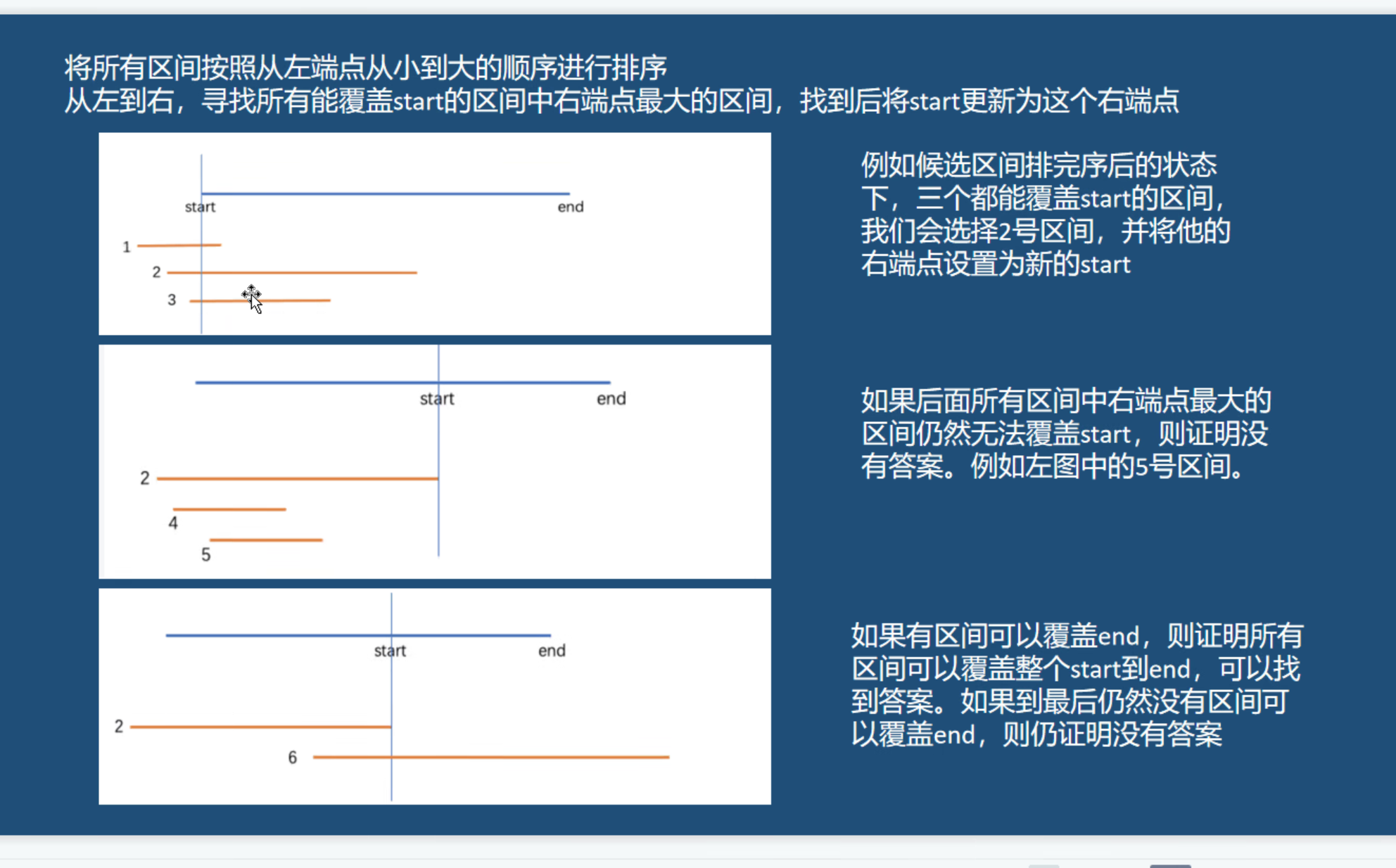
贪心模型三:区间覆盖问题
典型例题:区间覆盖
题目描述:数轴上有n个闭区间\([l,r]\),选择尽量少的区间覆盖一条指定线段区间\([Start,End]\)
思路:我们对各区间按照左端点升序排列,然后我们找出区间左侧端点小于st的最大的右端点r,如果r<st,说明无法覆盖,如果r>=st,我们就更新st的值为r,重复以上步骤,如果有一次我们发现st>=end,说明我们能覆盖指定区间,如果遍历完所有区间后,st依旧<end,我们就认为无法覆盖住区间
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
pii a[110];
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
while (cin >> n, n)
{
int st, ed;
cin >> st >> ed;
for (int i = 1; i <= n; ++i)
{
cin >> a[i].first >> a[i].second;
}
sort(a + 1, a + 1 + n); // 按照区间左端点升序排列
int flag = 0, r = -1;
for (int i = 1; i <= n; ++i)
{
if (a[i].first <= st)
r = max(r, a[i].second);//找到右端点最大的区间
else
{
if (r >= st) //如果比st大,则更新st
st = r;
else //否则,无法覆盖
break;
if (st >= ed) //代表能够覆盖
{
flag = 1;
break;
}
}
}
if (flag)
cout << "YES\n";
else
cout << "NO\n";
}
}
return 0;
}
贪心模型四:区间分组问题
典型例题:区间分组
题目描述:给定n个闭区间\([l,r]\),请你将这些区间分成若干组,使得每组内的区间两两之间(包括端点)没有交集,并且使得分得的组数尽可能小
思路:首先将这些区间按照左端点升序排列,我们设想如果现在有许多组,如果一个准备被分组的区间的左端点比所有已经分完组中的每个组的最右端点的最小值还要小,说明我们这个区间需要自己再开一组,如果比所有已经分完组中的每个组的最右端点的最小值大,说明它可以并入其他组,我们还需要去维护所有组最右端点的最小值,我们考虑使用优先队列维护
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
pii a[110];
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
while (cin >> n, n)
{
int st, ed;
cin >> st >> ed;
for (int i = 1; i <= n; ++i)
{
cin >> a[i].first >> a[i].second;
}
sort(a + 1, a + 1 + n); // 按照区间左端点升序排列
int ans = 0;
priority_queue<int,vector<int>,greater<int>> q;
for (int i = 1; i <= n; ++i)
{
if (!q.size() || a[i].first<=q.top()) //如果不能被分进先前的组,另开一组,并将右端点入列
{
ans++;
q.push(a[i].second);
}
else if (q.size() && a[i].first>q.top()) //如果可以被分进先前的组
{
q.pop(); //更新之前的组的右端点
q.push(a[i].second);
}
}
cout << ans << endl;
}
}
return 0;
}
贪心模型五:哈夫曼树模型

例题:合并果子
题目描述
在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过 \(n-1\) 次合并之后, 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 \(1\) ,并且已知果子的种类 数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
例如有 \(3\) 种果子,数目依次为 \(1\) , \(2\) , \(9\) 。可以先将 \(1\) 、 \(2\) 堆合并,新堆数目为 \(3\) ,耗费体力为 \(3\) 。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 \(12\) ,耗费体力为 \(12\) 。所以多多总共耗费体力 \(=3+12=15\) 。可以证明 \(15\) 为最小的体力耗费值。
输入格式
共两行。
第一行是一个整数 \(n(1\leq n\leq 10000)\) ,表示果子的种类数。第二行包含 \(n\) 个整数,用空格分隔,第 \(i\) 个整数 \(a_i(1\leq a_i\leq 20000)\) 是第 \(i\) 种果子的数目。
输出格式
一个整数,也就是最小的体力耗费值。输入数据保证这个值小于 \(2^{31}\) 。
样例输入 #1
3 1 2 9样例输出 #1
15提示
对于 \(30\%\) 的数据,保证有 \(n \le 1000\):
对于 \(50\%\) 的数据,保证有 \(n \le 5000\);
对于全部的数据,保证有 \(n \le 10000\)。
思路:体力最小值实际上就是哈夫曼数所有带权路径长度之和,即“WPL”,我们利用优先队列维护,我们始终找出队列中权重最小的两个子节点,将其加起来合成另一个节点,并将这个节点入列,最后还原出根节点,也就是队列中只有一个元素
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
cin >> n;
priority_queue<int, vector<int>, greater<int>> q;
for (int i = 1; i <= n; ++i)
{
int x;
cin >> x;
q.push(x);
}
ll sum = 0;
while (q.size() != 1)
{
int t = 0;
t += q.top(); //找出第一个权重最小的子节点
q.pop();
t += q.top(); //找出第二个权重最小的子节点
q.pop();
q.push(t); //将两个节点之和变成他们两个的父节点,并入列
sum += t;
}
}
return 0;
}
反悔贪心
不多说了,多做题吧,还是太菜了!


