HZNU Winter Trainning STL 补题
2023.01.03 HZNU Winter Trainning STL 补题
CodeForces - 4C
题意:给你n个字符串,如果某个字符串出现过,则在这个字符串后面加上1,2,3,4....以此类推
题解:利用map记录某个字符串出现次数,然后利用to_string函数即可
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
map<string, int> mp;
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
{
string s;
cin >> s;
if (mp[s] == 0)
{
mp[s]++;
cout << "OK\n";
}
else
{
mp[s]++;
cout << s + to_string(mp[s] - 1) << endl;
}
}
}
return 0;
}
CodeForces - 1526C2
题意:一个人的分数为1597,他想使他的分数增加,所以他需要打比赛,但是任何时候他不能使自己的分数低于1597,所以他需要跳过一些比赛,现在给你打的每一场能够加的分数(有可能使负数),请你计算出他最多能打几场比赛
题解:反悔贪心,优先队列实现。就是有些比赛可以假装打,后来遇到更小的比赛,直接后悔,如果比赛分数是正数直接加到sum中,如果比赛分数是负数,那么先判断如果加到sum中sum会不会<0,如果sum没有<0,那么我们直接加进去,如果<0了,我们看能不能跟现在队列里最小的元素换一下,这就是反悔的精髓,但是当时没有想明白为什么一开始是负数不行,后来仔细看题目,如果第一场是负数,他一定需要跳过,因为他任何时候的分数都不能低于1597,所以直接看代码。
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
priority_queue<ll, vector<ll>, greater<ll>> q; //小根堆实现优先队列
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
cin >> n;
ll sum = 0L;
for (int i = 1; i <= n; ++i)
{
ll x;
cin >> x;
if (x >= 0) //x>=0直接入列
{
sum += x;
q.push(x);
}
else
{
if (sum + x >= 0)
{
sum += x;
q.push(x);
}
else
{
if (q.size() && q.top() < x) //会不会反悔
{
sum -= q.top();
q.pop();
sum += x;
q.push(x);
}
}
}
}
cout << q.size() << endl;
}
return 0;
}
CodeForces - 1490F
Dzy有一个长度为 n 的数组 a 。Dzy认为,如果存在一个数字 C ,那么数组中的每个数字都会出现 0次或 C次,那么数组就是漂亮的。为了使数组变漂亮,dzy会从数组 a 中删除一些元素
例如,如果 n=6 且 a=[1,3,2,1,4,2]a=[1,3,2,1,4,2] ,则可以进行以下操作之一使数组 a 数组更漂亮:
删除位置 2 和 5 的元素,数组 a 变为等于 [1,2,1,2][1,2,1,2];
删除位置 1 和 6 的元素,数组 a 等于 [3,2,1,4][3,2,1,4] ;
删除位置 1 、 2和 6 处的元素,数组 a 变为等于 [2、1、4][2、1、4] ;帮助dzy确定要从数组 a 中删除的元素的最小数量,以使数组变漂亮。
t组输入,1<=t<=1e4,每行包括一个正数n,1<=n<=2e5,第二行n个数ai,1<=ai<=1e9;
题解:我们先来一个引理:假设数据量n,那么最多会有多少种出现次数?我们来看一个最坏的情况1 2 2 3 3 3 4 4 4 4 5 5 5 5 5.....,直到出现n个数,所以利用等差数列求和公式,假设出现x种,列出公式
所以我们就知道了,2e5个数实际上最多就632种出现次数
回到题目,首先这道题让我们把数组每个元素出现的次数变为一样,所以与元素的值无关,定义两个map我们先把每个元素出现的次数用map1统计,用map2统计每种出现次数的组数,直接看题目给的样例
我们遍历map2对每种出现次数我们进行如下操作:如果其他出现次数比该出现次数小,我们全部删除,否则我们删除多的部分,每次对ans取min维护ans,因为最多632种出现次数,所以最多4e5数量级
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
map<ll, int> mp1, mp2;
int main(void)
{
Zeoy;
int t = 1;
cin >> t;
while (t--)
{
mp1.clear();
mp2.clear();
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
{
ll x;
cin >> x;
mp1[x]++;
}
for (auto i : mp1)
mp2[i.second]++;
ll ans = inf;
for (auto it : mp2)
{
ll sum = 0L;
for (auto i : mp2)
{
if (i.first < it.first)
sum += i.first * i.second;
else
sum += (i.first - it.first) * i.second;
}
ans = min(ans, sum);
}
cout << ans << endl;
}
return 0;
}
CodeForces - 799B
题解:因为衣服颜色就三种,直接开3个set记录每个颜色有的衣服的价格,为什么开set呢?因为顾客还想要该颜色最便宜的衣服,如果选到了衣服,就在其余两个set种将同种价格的price删掉因为一件衣服正反面两种颜色
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
ll price[N];
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n;
cin >> n;
set<ll> st[4];
for (int i = 1; i <= n; ++i)
cin >> price[i];
for (int i = 1; i <= n; ++i)
{
int x;
cin >> x;
st[x].insert(price[i]);
}
for (int i = 1; i <= n; ++i)
{
int x;
cin >> x;
st[x].insert(price[i]);
}
int m;
cin >> m;
while (m--)
{
int x;
cin >> x;
if (st[x].size())
{
int p = *st[x].begin();
cout << p << " ";
for (int i = 1; i <= 3; ++i) //将其他set中的相同价格全部删除
st[i].erase(p);
}
else
cout << "-1 ";
}
cout << endl;
}
return 0;
}
Gym - 417661B 倒杨辉三角
题解:
看到数据范围直接考虑next_permutation枚举,先看样例
我们要知道16是可以有3 1 2 4推导出来的
我们通过正杨辉三角预处理出每个元素乘以的系数index,然后进行next_permutation遍历每种情况,如果找到就退出,a数组代表枚举的数组,如果出现
那就说明后面[i+1,n]不用再加了,直接跳过,怎么跳过呢?我们对[i+1,n]这段序列从大到小sort一下就能跳过了,这是细节
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
int a[50][50] = {0};
int main(void)
{
Zeoy;
int t = 1;
// cin >> t;
while (t--)
{
int n, num;
cin >> n >> num;
a[1][n] = 1;
for (int i = 2; i <= n; ++i)
for (int j = 1; j <= 2 * n - 1; ++j)
a[i][j] = a[i - 1][j - 1] + a[i - 1][j + 1];
vector<int> index;
for (int j = 1; j <= 2 * n - 1; ++j)
{
if (a[n][j] != 0)
index.push_back(a[n][j]);
}
vector<int> v;
for (int i = 1; i <= n; ++i)
v.push_back(i);
int isfind = 0;
do
{
int sum = 0;
int flag = 1;
for (int i = 0; i < n; ++i)
{
sum += v[i] * index[i];
if (sum > num)
{
sort(v.begin() + i + 1, v.end(), greater<int>());
flag = 0;
break;
}
}
if (flag && sum == num)
{
isfind = 1;
break;
}
} while (next_permutation(all(v)));
if (isfind)
{
for (auto i : v)
cout << i << " ";
cout << endl;
}
else
cout << "Not Found\n";
}
return 0;
}
[CodeForces - 1569D ](Problem - D - Codeforces)
题解:二分+离散化+思维
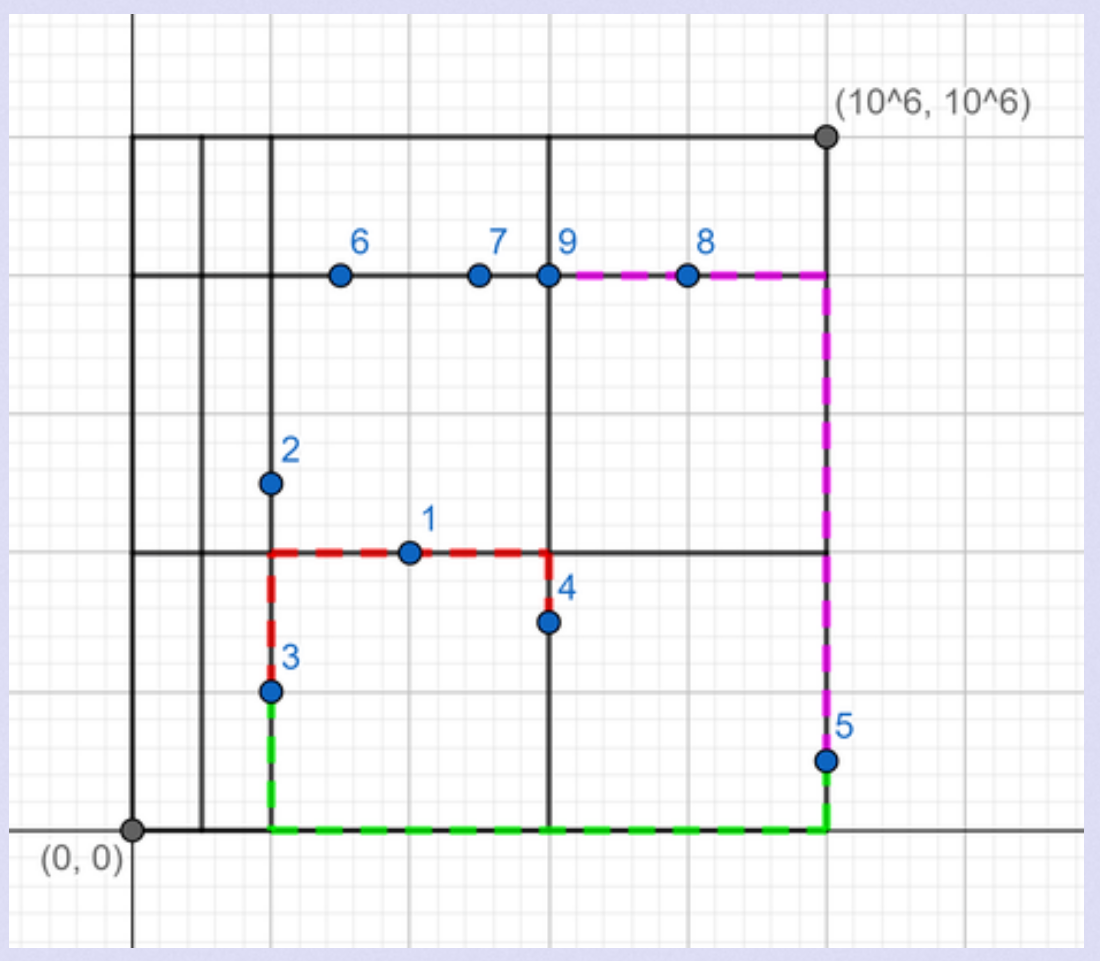
我们先看垂直X轴的直线,发现如果两个点被夹在两条平行于X轴的直线之间,最短距离就不是曼哈顿距离,比如3,4和4,5,但是如果某个点和其他点再同一条垂直于X轴的直线上不产生贡献,并且处于X,Y交点处的点也不产生贡献,所以以X纵线为例,并且题目保证给的纵线坐标和横线坐标是单增的,我们可以二分找到比这个点的y坐标大的第一条Y横线,然后对Y横线加贡献,但是为了防止初始化超时,我们离散化,直接将Y的下标作为这条直线,同理Y横线的地位和X纵线等价,所以处理方式一样
#include <bits/stdc++.h>
#define Zeoy std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define all(x) (x).begin(), (x).end()
#define endl '\n'
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
const double eps = 1e-9;
const int N = 2e5 + 10;
int lel[N]; // 水平直线坐标 对应y轴
int ver[N]; // 垂直直线坐标 对应x轴
int numx[N]; // 代表上有几个点被夹在两条垂直x轴的直线中间
int numy[N]; // 代表上有几个点被夹在两条垂直y轴的直线中间
map<pii, int> mpx, mpy; //代表在两线之间并且在一条直线上有几个点
int main(void)
{
Zeoy;
int t = 1;
cin >> t;
while (t--)
{
mpx.clear();
mpy.clear();
int n, m, k;
cin >> n >> m >> k;
for (int i = 1; i <= n; ++i)
{
cin >> ver[i];
numx[i] = 0; //离散化初始化很方便
}
for (int i = 1; i <= m; ++i)
{
cin >> lel[i];
numy[i] = 0;
}
ll ans = 0L;
for (int i = 1; i <= k; ++i)
{
pii p;
cin >> p.first >> p.second;
int x = lower_bound(ver + 1, ver + 1 + n, p.first) - ver; //落在哪条纵线上
int y = lower_bound(lel + 1, lel + 1 + m, p.second) - lel;//落在哪条横线上
if (p.first == ver[x] && p.second == lel[y]) //在两条线交点处
continue;
else if (p.first == ver[x] && p.second != lel[y]) //在纵线上
{
ans += (numy[y] - mpx[{x, y}]); //离散化很方便
numy[y]++;
mpx[{x, y}]++;
}
else if (p.first != ver[x] && p.second == lel[y]) //在横线上
{
ans += (numx[x] - mpy[{x, y}]);
numx[x]++;
mpy[{x, y}]++;
}
}
cout << ans << endl;
}
return 0;
}


