编译原理: FIRST(x) FOLLOW(x) SELECT(x)的计算

目录

• First计算
• Follow计算
• Select计算
• 判断是否是LL(1)文法
• 预测分析表的书写

已知文法G[S]：
           S→MH|a
           H→LSo|ε
           K→dML|ε
           L→eHf
           M→K|bLM
判断G是否是LL（1）文法。 

First计算

First集合的定义就是某个非终结符表达式可以推导出来的第一个字符可以是什么
比如表达式S --> abb,它的First(S)={a}

First(S)={a}+First(M)+First(H)+{ε}={a,b,d,e,ε}
# S表达式存在单个的终结符a,添加{a}
# S表达式以M开头,添加First(M)
# 根据后面的表达式判断,M可以推出K,K可以推出空,所以M可以为空,此时S以H开头,添加First(H)
# 由于H也可以推出空,所以S最终也会指向空,添加 空集
First(M)={b}+First(K)+{ε}={b,d,ε}
# M表达式以终结符b开头,添加{b}
# M表达式可以推导出单个的K表达式,所以添加First(K)
# K有可能推导出空集,即M可以推导出空,所以添加 空集
First(K)={d}+{ε}={d,ε}
# K可以以终结符d开头,添加{d}
# K可以推导出空,添加空集
First(H)=First(L)+{ε}={e,ε}
# H可以推导出以L开头的表达式,所以添加First(L)
# H可以推导出空,所以添加空集
First(L)={e}
# L只能推导出一个表达式,并且开头是终结符,所以添加{e}

## 最后将已知的表达式代入到未知的表达式当中去,即可求出全部First集合

Follow计算

Follow表示某个非终结符后面可以跟着什么样的字符
Follow集不存在空集
为表达式编号

1: S→MH|a
2: H→LSo|ε
3: K→dML|ε
4: L→eHf
5: M→K|bLM

Follow(S)={$}+{o}={o,$}
# 在表达式1中,S是一个非终结符,S是孤立的一个表达式,其Follow可以添加$,即添加{$}
# 在表达式2中,S后面跟上了o,所以添加{o}
Follow(H)=Follow(S)+{f}={f,o,$}
# 在表达式1中,S后面跟了什么,MH后面就跟了什么,所以添加Follow(S)
# 在表达式4中,H后面跟了f,所以添加{f}
Follow(M)=First(H)+Follow(S)+First(L)={e,o,$}
# 在表达式1中,M后面跟了H,所以添加First(H)
# 在表达式2中可知,H可以推导出空,所以回到表达式1,S后面跟了什么,M后面就跟了什么,所以添加Follow(S)
# 在表达式3中,M后面跟了非终结符L,所以添加First(L)
# 在表达式5中,M后面跟了什么,bLM后面就跟什么,都是Follow(M),表达式不变
Follow(L)=First(S)+Follow(K)+{o}+{$}+First(M)+Follow(M)={a,b,d,e,o,$}
# 在表达式2中,L后面跟了非终结符S,所以添加First(S)
# 在表达式2中,First(S)可以推出空,所以此时L后面跟着o,添加{o}
# 在表达式3中,K后面跟了什么,dML后面就跟了什么,所以添加Follow(K)
# 在表达式4中,L属于单一元素,所以添加$
# 在表达式5中,L后面跟上了非终结符M,所以添加First(M)
# 在表达式5中,从上得知,First(M)可以推导出空,所以此时M后面跟着什么,L后面就要跟着什么,所以添加Follow(M)
Follow(K)={$}+Follow(M)={e,o,$}
# 在表达式3中,K是单一字符,添加{$}
# 在表达式5中,M后面跟着什么,K后面就跟着什么,所以添加Follow(M)

注意:在书写Follow集中要时刻检查First集是否可以为空.

Select计算

分割表达式,如果非空则是First集,是空则为Follow集

Select(S→MH)=First(M)+First(H)+Follow(S)={b,d,e,o,$}
# S以M开头,加入First(M)
# First(M)可以为空,加入First(H)
# M和H都可以为空,加入Follow(S)
Select(S→a)={a}
# S只能推导出a,加入{a}
Select(H→LSo)=First(L)={e}
# H以L开头,并且First(L)不可以为空,即加入First(L)
Select(H→ε)=Follow(H)={f,o,$}
# H推导出空,加入Follow(H)
Select(K→dML)={d}
# K以终结符d开头,加入{d}
Select(K→ε)=Follow(K)={e,o,$}
# K可以为空,加入Follow(K)
Select(L→eHf)={e}
# L以终结符e开头,加入{e}
Select(M→K)=First(K)+Follow(M)={d,e,o,$}
# M可以推出K,加入First(K)
# First(K)可以为空,即M可以加入Follow(M)
Select(M→bLM)={b}
# M可以推出以终结符b开头,加入{b}

判断是否是LL(1)文法

LL(1)文法就是同一非终结符推出来的Select集合相交为空，现在开始逐一判断

Select(S→MH)∩Select(S→a)
Select(H→LSo)∩Select(H→ε)
Select(K→dML)∩Select(K→ε)
# L只有一个表达式，省略L
Select(M→K)∩Select(M→bLM)

易知，上述表达式都为空，所以这个表达式是LL(1)文法

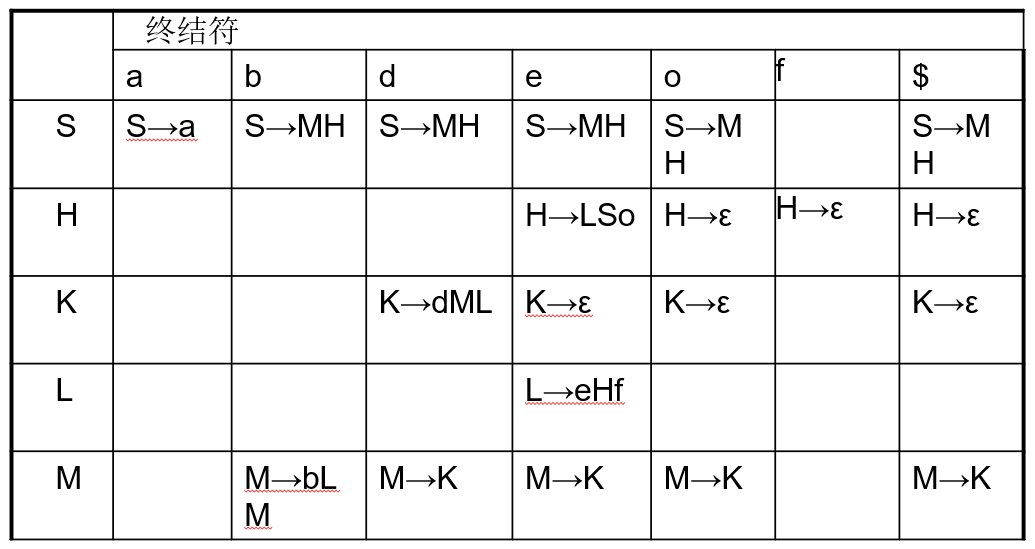
预测分析表的书写

先列出First集和Follow集的表格

	First	Follow
S
H
K
L
M

然后将非终结符、终结符作为横纵行，填入表达式