吴恩达机器学习之逻辑回归的课堂复习笔记

总结吴恩达机器学习第三周的内容

写在前面：
机器学习小白小菜鸡，如果文章有什么错误还希望读者积极批评！
或者教我一些知识那是最好啦
觉得我写的还可以的点个赞鼓励鼓励我谢谢各位。

分类问题Classification

在日常生活中的实际问题中，往往只有“是”和“否”两个选项。例如，处理邮件时，我们只要判断它是否是垃圾邮件，并没有既不是垃圾邮件也不是useful的邮件。再比如逻辑电路中，我们只有开和关两种状态，所以我们用0或者1来表示电路的开关。同样，引申出来，我们用1和0来表示实际问题的“是”和“否”。（当然对于多种情况在之后会讲到用0、1、2、3……等来表示相应情况，先只讨论‘是’和‘否’两种结果）
吴恩达在课程中沿用了良性肿瘤和恶性肿瘤的例子，‘1’表示良性，‘0’表示恶性。

在这个图像的讲解中，红叉代表的是训练实例。很显然，随着肿瘤的大小逐渐增大，是恶性肿瘤的可能就变大。它像以前的课程一样使用线性回归来拟合这些离散的点。

它规定，如果最后得恶性肿瘤的概率大于等于0.5，就认为它是恶性肿瘤。反之，就认为它不是恶性肿瘤。

所以在这一类问题中，我们引出了逻辑回归的概念。
逻辑回归，只有对应几个的逻辑值（此处是两个：‘0’和‘1’），并且回归函数必须介于[0,1]中，表示概率。

这类问题也可以成为 ：二进制分类问题binary classification problem

---

假设函数的表示Hypothesis Representation

在这堂课中，吴恩达突然发出一个假设函数：
如果想要函数因变量介于1和0之间：
令h（x）=g（θ转置*x）
于是衍生出g（z）

带入得到h（x）

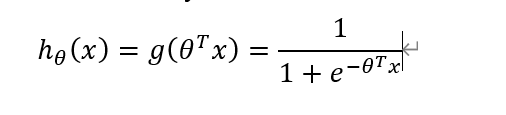
为什么要提出这样的一个函数？
是应为在g（z）这个函数中，符合逻辑回归的要求：必须介于0和1 之间。
视频里叫它s型函数（Sigmoid Function）

引出这个函数之后，他开始预测得恶性肿瘤的概率

x0是永远等于1 的。
假设最后算出来的结果是0.7，就表明这个人得恶性肿瘤的概率就是0.7。

他还强调了一下，概率之和为1。
于是我们可以总结一下，我们引入了这个假设函数，通过假设函数可以大致得算出它得恶性肿瘤的概率。

---

决策边界Decision Boundary

和上上节说的一样，为了实现二进制分类，我们规定了标准：
hθ(x)≥0.5→y=1
hθ(x)<0.5→y=0
根据函数图像，我们可以知道，当输入的z值大于0的时候，对应的假设函数的输出的值大于0.5.

所以推导出来关系：

结果已经很明白了对吧。
所以决策边界是干嘛的呢？就是一个分类用的线罢了！
用来判断它到底是y=1还是y=0

甚至根据z的复杂程度，可以诞生出不同的决策边界

总结一下：决策边界就是一个用来分类的线，随着z的复杂程度的增加，决策边界可以愈发得“扭曲”……

---

逻辑回归中的代价函数（重点）

对于线性回归的代价函数：

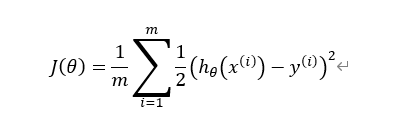
是这样的，大概是一个凹函数（其实我也搞不清楚叫什么，怎么好理解怎么来吧）。在线性回归中，我们致力于找到一个最小的“代价”，来求得相应系数的值。
我所理解的代价是指它这个线偏离实际数据的距离大小程度，代价越大，线拟合得越离谱。
所以我们也需要找到这个代价函数来确定相应的系数θ1，θ2……
但是根据线性回归的代价函数来表示逻辑回归的代价函数的话，得到的确实这样的一幅图：

原因是逻辑回归是一个s型的函数，得出来的代价函数看起来几乎不可能找到最小的代价。所以有问题就是要改变。
首先，吴恩达将代价函数后面的部分换了个名字，方便理解吧：

然后引入新的代价函数：

这两个代价函数来的猝不及防。意料之外，却是在情理之中（废话）
吴恩达给出了这两个函数的图像：

图像十分容易解释：
当y=1的时候，即确定它是恶性肿瘤的时候，我们只需要花很少的代价就可以拟合它是和1很相近的函数。同理当y=0的时候，我们也只需要花很少的代价就可以得到它是良性肿瘤，并且要花无穷大的代价去确认它是恶性肿瘤，谁会去花费一个无穷大的代价去得到一个错误的结果呢？

---

简化代价函数和梯度下载Simplified Cost Function and Gradient Descent

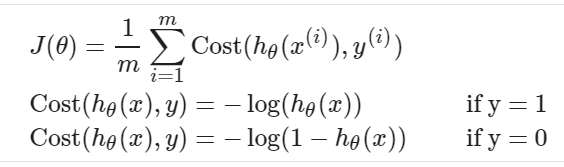
这两个式子看起来莫过于繁琐，所以吴恩达简化了该式子（两个if语句简化为一个if语句）

带入到代价函数中去：

对其矢量化（方便MATLAB操作）

于是代价函数就出来了。
但是有代价函数还远远不够，我们最后要求的参数还是需要梯度下降的支持（虽然后面又说其他的算法好）

循环更新这个系数，最后得到一个较为准确的值

---

高级优化Advanced Optimization

讲新的算法了，这些算法可以用MATLAB或者octave中的函数进行调用：

“Conjugate gradient”, “BFGS”, and “L-BFGS” are more sophisticated,

function [jVal, gradient] = costFunction(theta)
  jVal = [...code to compute J(theta)...];
  gradient = [...code to compute derivative of J(theta)...];
end

options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

通过这些代码可以求得代价函数以及θ的矩阵。后期进行实操的是候还需要多加练习。

---

一对多的分类Multiclass Classification: One-vs-all

前面一直介绍只有两种可能性的事件，我们很自然地把他们分别记为‘0’或者‘1’
但是对于很多的事情来说，往往一件事情有多种可能，那么我们应该如何去分类呢？

吴恩达列举了三个可能的事件的分类方法，就是逐个分类，n种类分类n次。
当然随着分类的增多，我们的代价函数肯定是要随之改变的。