吴恩达机器学习之正则化的课堂学习笔记

过拟合问题The Problem Of Over Fitting

过拟合问题，顾名思义，就是拟合得过度了。但是不禁要有人问，拟合得不是越贴切越好吗，怎么还能拟合过度了呢？一开始看到这个标题我就有这样的疑问。

仍然是房地产的例子。有五个关于房地产的数据
在第一幅图中，又一条直线粗略得去拟合这些数据，显而易见，这些数据都不在这条直线上，代价函数可见相当的大，如果使用这个模型得出的结论肯定也不够准确，这叫做欠拟合。

在第二幅图中，他用曲线去拟合了这些数据，看起来十分的贴切，似乎这就是最佳的方案了，但是受于函数本身的次幂图像的限制，并不是所有的点都能在这条曲线上。

要使所有的点都在这条曲线上，肯定需要更加复杂的曲线，但是如图三所示，数据都是在这条曲线上了，代价函数约等于0，但是这曲线看起来是异常的“扭曲”，并且直观的感受这个曲线不如第二幅图里面的曲线好，肯定得出来的结论的准确率不高，这就是过拟合。
所以我认为的过拟合的概念是：过度得去追求数据在函数上而提高函数次幂导致函数图像变得复杂且不够准确。

上面是线性回归的例子，吴恩达又开始讲逻辑回归的例子

主要传达的思想是大同小异的，这里就不再过分赘述。

那为了防止它过度拟合，吴恩达列举了一下几种方法：

分别是：
减少变量的数（比如最高次幂的下降）：

• 手动减少变量的数
• 使用模型选择算法（之后会讲解）

正规化：

• 保留所有的变量，但是减少系数的大小
• 当我们有很多稍微有用的功能时，正规化效果更好。

于是引出了下一课堂的学习

---

正规化之代价函数Cost Function

在这个图中，想要从后者变成前者，我们可以手动删除相应的变量

在这个图中，他想解释的是，我们还可以让系数的值变得足够小，让它对代价函数的影响非常小。
于是就解释了上节课讲的两种方法：

• 手动减少变量的数
• 保留所有的变量，但是减少系数的大小

由于我们更新θ的时候，在代价函数的偏导前面是一个负号，所以我们增大代价函数的值，可以相应减少所更新的θ：

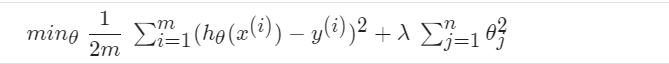
我们在代价函数的后面加上了一个多项式，可以相应增大的代价函数的大小，防止过拟合。
那么这个λ应该怎么去决定呢？？

显而易见，如果λ=0或者太小，对这个多项式那就没什么用了。
所以我们讨论λ太大的时候：如果λ太大的话（比如一百亿），那么它就会通过一下式子不断消除更新，导致更新出来的θ十分得小

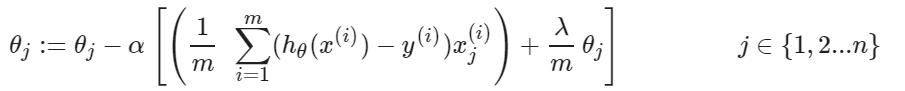
我们默认不去改变这个θ0，所以j是从1开始的
最后的图像会变成一下这个样子：

很明显，这是欠拟合的。
总结一下：我们为了减少θ的更新，去在代价函数后面添加多项式，但是这个多项式不宜过大，不然对θ的更新影响太大，导致θ为0，得出错误的结论。

---

线性回归的正规化Regularized Linear Regression

在上一节其实把正规化讲的差不多了。

引入多项式的目的是为了不断去减少θ。默认不改变θ0，j是从1开始的。于是可以得出：

这样的写法，再把第二个式子进行一个整理：

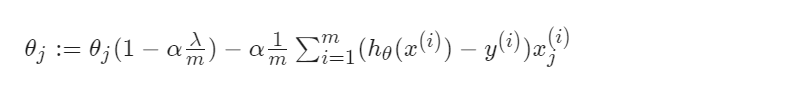
吴恩达强调，这个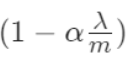一般都是小于1的，毕竟λ不能超过数据集，不然没有意义（自变量的最大值就是数据集的数值）。
他还告诉我们关于矩阵的写法，方便我们写代码：

---

正规化逻辑回归Regularized Logistic Regression

换汤不换药

假设x1和x2都是有用的，我们只能减少各种θ的数值：

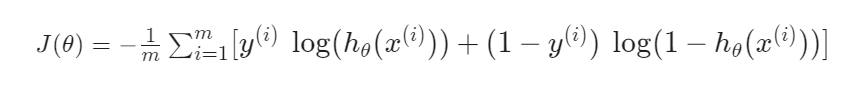
这个是逻辑回归的代价函数，和线性回归一样，在后面加上多项式来抵消θ的更新：

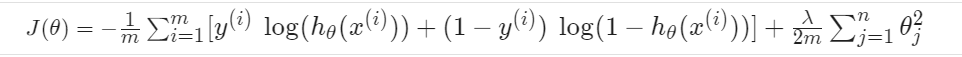
然后就没有什么新东西了。

下一章开始讲神经网络了，当然在此之间我还会写一些关于前面的知识进行一个复习，还有编程作业等等，希望各位大佬批评指正。