数据结构与算法 --线性表及其顺序存储

线性表的特点：

线性表是一个线性结构，它是一个含有0个或者多个节点的有限序列，对于其中的节点，

有且只有一个开始节点，它没有前驱但有一个后继节点。

有且只有一个终端节点，它没有后继但有一个前驱节点。

其他的节点都有且仅有一个前驱和一个后继节点。

通常一个线性表可以表示成一个线性序列：k1，k2，……，kn。其中k1是开始结点，kn是终端结点。

 

 

顺序表的定义：

线性表采用顺序存储的方式存储就称为顺序表。顺序表是将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。

 

顺序表的实现：

 #define MAXSIZE 100
 typedef int datatype;
 typedef struct{
   datatype a[MAXSIZE];
   int size;
 }sequence_list;

 

顺序表的初始化：

void initseqlist(sequence_list *L)
{    L->size=0;
}

 

在顺序表的后部插入操作：

void append(sequence_list *L,datatype x)
{
   if (L->size==MAXSIZE)
      {
         printf("顺序表是满的");
         exit(1);
      }
   L->a[L->size]=x;
   L->size=L->size+1;
}

 

打印顺序表各节点的值：

void print(sequence_list *L)
{   int i;
    for (i=0;i<L->size;i++)
       {    printf("%5d",L->a[i]);
            if ((i+1)%10==0) printf("\n");
       }
    printf("\n");
}

 

输入顺序表：

void input(sequence_list *L)
{  datatype x;
   initseqlist(L);
   printf("请输入一组数据，以0做为结束符：\n");
   scanf("%d",&x);
   while (x)
       {    L->a[L->size++]=x;
             scanf("%d",&x);
         }
}

 

判断顺序表是否为空：

int empty(sequence_list L)
{
   return (L.size==0 ? 1:0);
}

 

找查顺序表中值为x的结点位置：

int find(sequence_list L,datatype x)
{
   int i=0;
   while(i<L.size  && L.a[i]!=x)
      i++;
   return (i<L.size? i:-1);
}

 

取得顺序表中的第i个结点的值：

datatype get(sequence_list L ,int i)
{
   if(i<0 ||i>=L.size)
   {
      printf("找不到指定的位置");
      exit(1);
   }
   else
   {
      return L.a[i];
   }
}

 

从文件中输入顺序表：

void inputfromfile(sequence_list *L,char *f)
{  int i,x;
   FILE *fp=fopen(f,"r");
   L->size=0;
   if (fp)
   {   while ( ! feof(fp))
        {
            fscanf(fp,"%d",&L->a[L->size++]);
        }
        fclose(fp);
   }
}

 

顺序表的插入操作：插入后元素依次后移。

void insert(sequence_list *L,datatype x,int position)
{
   int i;
   if(L->size==MAXSIZE)
   {
      printf("顺序表示满的！");
      exit(1);
   }
   if(position<0 || position >L->size)
   {
      printf("指定的插入位置不存在");
   }
   for(i=L->size;i>position ;i--)
   {
      L->a[i]=L->a[i-1];
      L->a[position]=x;
      L->size++;
   }
}

 

顺序表的删除操作：删除某个位置后向前移动。

void dele(sequence_list *L,int position)
{
   int i;
   if(L->size==0);
   {
      printf("顺序表是空的，无法删除元素");
      exit(1);
   }
   if(position <0 ||position>=L->size)
   {
      printf("顺序表的删除位置不对");
      exit(1);
   }
   for(i=position;i<L->size-1;i++)
   {
      L->a[i]=L->a[i+1];
   }
   L->size--;
}

 

顺序表的就地转置：

/**********************************/
/*文件名称：lab1-01.c             */
/**********************************/
/*基于sequlist.h中定义的顺序表，编写算法函数reverse(sequence_list *L)，实现顺序表的就地倒置。*/
#include "sequlist.h"
/*请将本函数补充完整，并进行测试*/
void reverse(sequence_list *L)
{
    int i;
    int len = L->size;
    for(i=0;i<len/2;i++) {
        int temp ;
        temp = L->a[i];
        L->a[i] = L->a[len-i-1];
        L->a[len-i-1] = temp;
    }
}

 

奇数偶数分别存放：

/**********************************/
/*文件名称：lab1_02.c             */
/**********************************/

/*编写一个算法函数void sprit( sequence_list *L1,sequence_list *L2,sequence_list *L3)，
将顺序表L1中的数据进行分类，奇数存放到存到顺序表L2中，偶数存到顺序表L3中，编写main()进行测试。
*/

#include "sequlist.h"
/*请将本函数补充完整，并进行测试*/
void sprit(sequence_list* L1, sequence_list* L2, sequence_list* L3)
{
    initseqlist(L2);
    initseqlist(L3);
    int i;
    for (i = 0; i < L1->size; i++) 
    {
        if ((L1->a[i]) % 2) 
        {
            L2->a[(L2->size)++] = L1->a[i];
        }
        else 
        {
            L3->a[(L3->size)++] = L1->a[i];
        }
    }
}

 

数据合并，升序存放：

/*已知顺序表L1，L2中数据由小到大有序，请用尽可能快的方法将L1与L2中的数据合并到L3中，使数据在L3中按升序排列。*/

#include "sequlist.h"
#include <stdlib.h>
/*请将本函数补充完整，并进行测试*/

void merge(sequence_list* L1, sequence_list* L2, sequence_list* L3)
{
    initseqlist(L3);
    int i, j;
    int len1 = L1->size;
    int len2 = L2->size;
    int pos1 = 0;
    int pos2 = 0;
    int flag = 0;
    for (i = 0; i < len1 + len2; i++)
    {
        if (L1->a[pos1] < L2->a[pos2])
        {
            L3->a[L3->size++] = L1->a[pos1++];
        }
        else if (L1->a[pos1] > L2->a[pos2])
        {
            L3->a[L3->size++] = L2->a[pos2++];
        }
        else if (L1->a[pos1] == L2->a[pos2])
        {
            L3->a[L3->size++] = L1->a[pos1];
            pos1++;
            pos2++;
        }
        if (pos1 >= len1 || pos2 >= len2) {
            flag = 1;
            break;
        }
    }

    if (flag)
    {
        if (pos1 >= len1)
        {
            for (pos2; pos2 < len2; pos2++)
                L3->a[L3->size++] = L2->a[pos2];
        }
        else if (pos2 >= len2)
        {
            for (pos1; pos1 < len1; pos1++)
                L3->a[L3->size++] = L1->a[pos1];
        }
    }
}

 

交集存放：

/*假设顺序表la与lb分别存放两个整数集合，函数inter(seqlist *la,seqlist *lb,seqlist *lc)
的功能是实现求顺序表la与lb的交集存放到顺序表lc中,请将函数补充完整.  */

/**********************************/
/*文件名称：lab1_04.c                 */
/**********************************/
#include "sequlist.h"
/*请将本函数补充完整，并进行测试*/
void  inter(sequence_list* la, sequence_list* lb, sequence_list* lc)
{
    int len1 = la->size;
    int len2 = lb->size;
    initseqlist(lc);
    int i, j;
    for (i = 0; i < len1; i++)
    {
        for (j = 0; j < len2; j++)
        {
            if (la->a[i] == lb->a[j])
            {
                lc->a[lc->size++] = la->a[i];
                break;
            }
        }
    }
}

 

奇数偶数分开两边：

/*
请编写一个算法函数partion(sequence_list *L)，尽可能快地将顺序表L中的所有奇数调整到表的左边，
所有偶数调整到表的右边，并分析算法的时间复杂度。
*/
/**********************************/
/*文件名称：lab1_05.c                 */
/**********************************/
#include "sequlist.h"
/*请将本函数补充完整，并进行测试*/
void partion(sequence_list* L)
{
    int len = L->size;
    sequence_list Ltemp1;
    sequence_list Ltemp2;
    initseqlist(&Ltemp1);
    initseqlist(&Ltemp2);
    int i;
    for (i = 0; i < len; i++)
    {
        if (L->a[i] % 2)
        {
            Ltemp1.a[Ltemp1.size++] = L->a[i];
        }
        else
        {
            Ltemp2.a[Ltemp2.size++] = L->a[i];
        }

    }

    initseqlist(L);
    int len1 = Ltemp1.size;
    int len2 = Ltemp2.size;
    for (i = 0; i < len1; i++)
    {
        L->a[L->size++] = Ltemp1.a[i];
    }
    for (i = 0; i < len2; i++)
    {
        L->a[L->size++] = Ltemp2.a[i];
    }
}

 

 

栈的特点：

栈是一种特殊的线性表，对于这种线性表，规定它的插入运算和删除运算均在线性表的同一端进行，进行插入和删除的那一端称为栈顶，另一端称为栈底。栈的插入操作和删除操作分别称为进栈和出栈。

栈具有先进后出的特点

 

中缀表达式和后缀表达式的互转：

中缀表达式就是我们常用的算式表达式。

后缀表达式适用计算机，可以减少计算机的运算量。

例如：a+b*c

后缀表达式就是abc*+；

 

转换方法：去括号法

首先假设我们需要转化的中缀表达式为：a + b * c + ( d * e + f ) * g

1：按照运算符的优先级对所有的运算单位加括号~

（（a +（b * c））+（（（d * e + f ）* g ））

2：把运算符号移动到对应的括号后面

((a(bc)*)+(((de)*f)+g)*)+

3：把括号去掉：

abc*+de*f+g *+

后缀式子出现

 

循环队列的特点

所以我们只来讨论循环队列的对空和对满的条件

普通的队空和队满的成立条件的都是front==rear，为了区别开来，我们损失一个队的存储空间不用，即当循环队列中的元素个数为MAXSIZE-1即为队满。损失的那个用front指向。

 

 

 

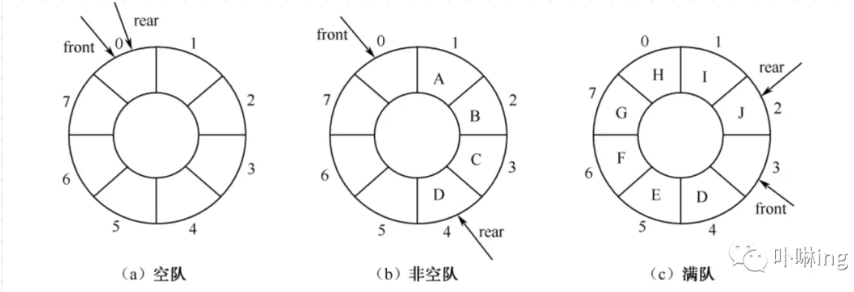
如图所示的图为元素 A、B、C 出队，元素 E、F、G、H、I、J 依次入队后队满的情况。此时 front = 3 , rear=2 ,  两者比较的结果为（rear+1）%MAXSIZE== front (即(2+ 1)%  8 == 3 ) , 所以循环队列为满。

所以当：

（rear+1）%MAXSIZE==front

的时候队满。

所以队空的条件是：

front==rear