数据结构与算法--概论复习

什么是数据结构？？

数据结构就是指按照一定的逻辑结构组成的一批数据，使用某种存储结构将这批数据存储于计算机中，并在数据上定义了一个运算集合。

 

逻辑结构和存储结构的一般分类：

逻辑结构：数据与数据之间存在的内在联系（或者称逻辑关系）。

（1）集合结构

（2）线性结构

（3）树形结构

（4）图形结构

存储结构：数据在计算机中的存储方式。

（1）顺序存储

（2）链式存储

（3）索引存储：建立索引表

（4）散列存储：函数式的存储方式。

运算集合：为一批数据定义的所有计算（或者操作）构成一个运算（操作）集合。

插入、删除、查找、输出、排序。

 

算法的五个特征：

1，有穷性 ：算法必须在有限步内结束

2，确定性 ：算法的每一个步骤必须是确定的，无二义性的。

3，输入 ：算法可以有0个或者多个输入

4，输出 ：算法一定有输出结果

5，可行性 ：算法中的运算必须是可以实现的

 

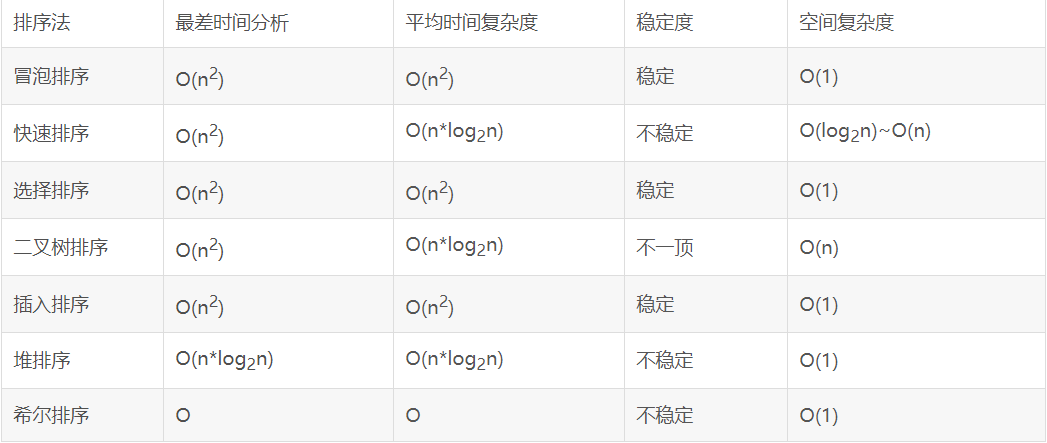
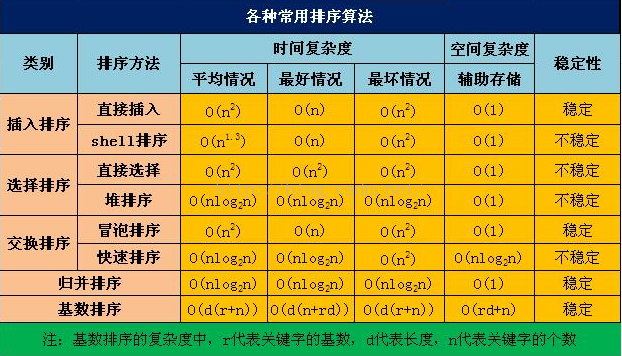
算法的时间复杂度和空间复杂度：

 

常用算法的时间复杂度和空间复杂度：

 

 

 

算法的时间复杂度的定义：

  在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。

算法的时间复杂度，也就是算法的时间量度。

记作：T(n)=O(f(n))。

它表示随问题n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐进时间复杂度，简称为时间复杂度。

其中，f(n)是问题规模n的某个函数

这样用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。

在各种不同算法中，若算法中语句执行次数为一个常数，则时间复杂度为O(1)。另外，在时间频度不相同时，时间复杂度有可能相同，如 T(n)=n^2+3n+4 与 T(n)=4n^2+2n+1 它们的频度不同，但时间复杂度相同，都为O(n^2)。

按数量级递增排列，常见的时间复杂度有：常数阶O(1) , 对数阶O(log2n) , 线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n^2)，立方阶O(n^3),...， k次方阶O(n^k),指数阶O(2^n)。

随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。

 

具体情况在之后的做题里再详细分析.

常用的时间复杂度所耗费的时间从小到大依次是：

 

 

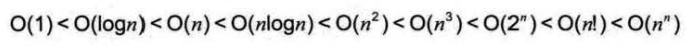
最坏情况与平均情况

我们查找一个有n 个随机数字数组中的某个数字，最好的情况是第一个数字就是，那么算法的时间复杂度为O(1)，但也有可能这个数字就在最后一个位置上待着，那么算法的时间复杂度就是O(n)，这是最坏的一种情况了。
最坏情况运行时间是一种保证，那就是运行时间将不会再坏了。 在应用中，这是一种最重要的需求， 通常， 除非特别指定， 我们提到的运行时间都是最坏情况的运行时间。
而平均运行时间也就是从概率的角度看， 这个数字在每一个位置的可能性是相同的，所以平均的查找时间为n/2次后发现这个目标元素。平均运行时间是所有情况中最有意义的，因为它是期望的运行时间。也就是说，我们运行一段程序代码时，是希望看到平均运行时间的。可现实中，平均运行时间很难通过分析得到，一般都是通过运行一定数量的实验数据后估算出来的。一般在没有特殊说明的情况下，都是指最坏时间复杂度

 

算法空间复杂度

我们在写代码时，完全可以用空间来换取时间，比如说，要判断某某年是不是闰年，你可能会花一点心思写了一个算法，而且由于是一个算法，也就意味着，每次给一个年份，都是要通过计算得到是否是闰年的结果。 还有另一个办法就是，事先建立一个有2050个元素的数组(年数略比现实多一点)，然后把所有的年份按下标的数字对应，如果是闰年，此数组项的值就是1，如果不是值为0。这样，所谓的判断某一年是否是闰年，就变成了查找这个数组的某一项的值是多少的问题。此时，我们的运算是最小化了，但是硬盘上或者内存中需要存储这2050个0和1。这是通过一笔空间上的开销来换取计算时间的小技巧。到底哪一个好，其实要看你用在什么地方。
算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作:S(n)= O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。
一般情况下，一个程序在机器上执行时，除了需要存储程序本身的指令、常数、变量和输入数据外，还需要存储对数据操作的存储单元，若输入数据所占空间只取决于问题本身，和算法无关，这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数，则称此算法为原地工作，空间复杂度为0(1)。
通常， 我们都使用"时间复杂度"来指运行时间的需求，使用"空间复杂度"指空间需求。当不用限定词地使用"复杂度'时，通常都是指时间复杂度。