poj 1912 A highway and the seven dwarfs

A highway and the seven dwarfs

Time Limit: 8000MS		Memory Limit: 30000K
Total Submissions: 2622		Accepted: 535
Case Time Limit: 3000MS

Description

Once upon a time, there was a land where several families of dwarfs were living. This land was called Dwarfland. Each family lived in one house. Dwarfs were often visiting their friends from the other families. Because the Dwarfland was free of evil, it happened that each dwarf visited each other during some short period of time. 

Once, the humans living in countries around Dwarfland decided to build several straight highways. As the humans weren't aware of the dwarfs, some of the planned highways passed through Dwarfland. The dwarfs discovered this and were quite unhappy about it. The dwarfs are very little, and also very slow, so they are unable to cross the highway safely. 

The dwarfs managed to get the plans for the highways somehow, and now they need your help. They would like to keep on visiting each other, so they don't like those highways which divide their houses into two non-empty parts. After they find out which highways they don't like, they will magically prevent the humans from building them. 

The dwarfs are very little, and cannot reach the keyboard. So they asked for your help. 

Task 

Given is a number N of points (houses) in the plane and several straight lines (highways). For each given line, your task is to determine whether all N points lie on the same side of the line or not. Your program has to output the answer for the currently processed line before reading the description of the next one. You may assume that no highway passes through any of the houses. 

Input

Your program is supposed to read the input from the standard input and write its output to the standard output. The first line of the input contains one integer N ( 0 < = N < = 100 000). N lines follow, the i-th of them contains two real numbers xi, yi ( -10⁹ < = xi, yi < = 10⁹) separated by a single space - the coordinates of the i-th house. 

Each of the following lines contains four real numbers X1, Y1, X2, Y2 ( -10⁹ < = X1, Y1, X2, Y2 < = 10⁹) separated by a single space. These numbers are the coordinates of two different points [X1, Y1] and [X2, Y2], lying on the highway.

Output

For each line of input, your program is supposed to output a line containing the string "GOOD" if all of the given points are on the same side of the given line, or "BAD" if the given line divides the points.

Sample Input

4
0.0 0
6.00 -0.001
3.125 4.747
4.747 0.47
5 3 7 0
4 -4.7 7 4.7
4 47 4 94

Sample Output

GOOD
BAD
BAD

Hint

Huge input,scanf is recommended. 

 

 

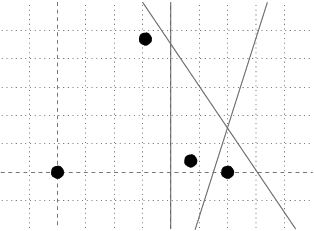
题意：给定平面上几个点的坐标，再给出一条直线，判断这条直线是不是能把点分离成两部分

思路：先找平面上这些点的凸包，那么要是凸包和直线相交，则直线肯定可以把点分离成两部分，问题的关键在于判断直线是否和凸包相交。

可以将凸包的每条边以及直线都考虑成向量的形式，那么凸包的边所形成的向量在极坐标系下的极角大小变化一定是单调的，可以看下图：

　　　　　　

 

 

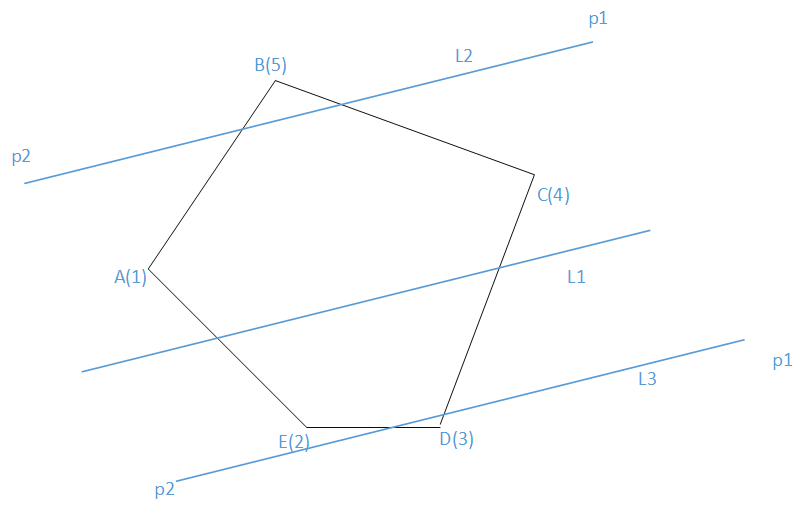
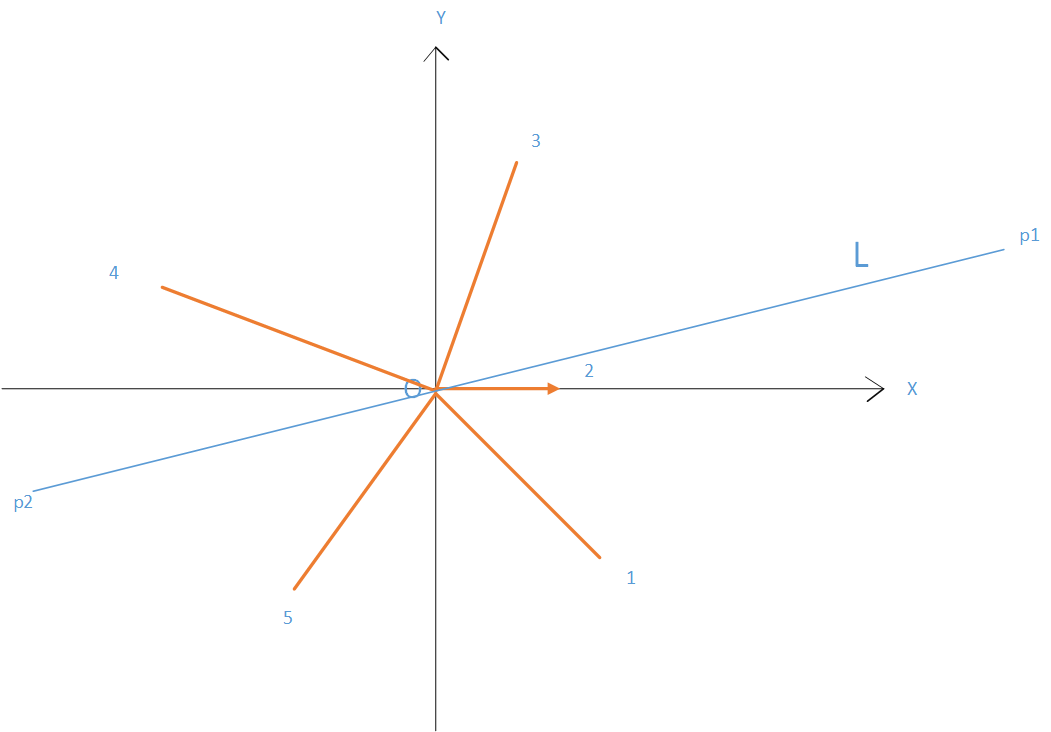
第一幅图中，向量ＡＥ，ＥＤ，ＤＣ，ＣＢ，ＢＡ的极角在 坐标系中变化是单调的，于是把他们都移到图二中来，都以Ｏ点为起点，按照极角大小排序并编号，凸包的算法因人而异，我现在用的凸包算法是以最左端的Ａ点开始存储，并按照逆时针方向存储点的，那么ＡＥ向量最好标记为极角最小的向量，ＥＤ次之，以此类推，那么我们就得设定极角的变化范围为（－９０，２７０］，这样将所有的向量排好序，并标记好编号，譬如右图的１向量代表ＡＥ向量。。。现在又给出一条直线L１，如何得知L１和凸包相交呢？我们平移L１的向量形式，移到Ｌ１只割掉了凸包一个点的位置（一共两个位置），Ｌ２的方向为ｐ１ｐ２，Ｌ３的方向为ｐ２ｐ１，我们发现这两条向量如果都要逆时针转一个方向，分别转动到向量ＤＣ和向量ＢＡ的位置需要转动的角度是最小的，而向量ＤＣ和ＢＡ的端点Ｄ，Ｂ又恰恰是向量Ｌ３和L１所割掉的点那么如果线段ＤＢ和直线Ｌ１有交点，则Ｌ１一定和凸包存在交点的。这个规律放到图二来看，直线Ｌ的向量形式为ｐ２ｐ１，转到向量３是所转角度最小的，其反向的向量转到向量５转角度又是最小的，向量３与向量５都是可以通过二分查找找出来，找到向量之后在取其起始端点，判断这两个起始端点是否与直线相交。

ＡＣ代码：

#define _CRT_SECURE_NO_DEPRECATE
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<queue>
#include<set>
#include<vector>
#include<cstring>
#include<string>
#include<functional>
#include<cmath>
#include<stack>
using namespace std;
const int N_MAX = 100000 + 5;
#define INF 0x3f3f3f3f
#define EPS 1e-10
#define equals(a,b) (fabs(a-b)<EPS)
#define pi acos(-1.0)
#define BOTTOM 0
#define LEFT 1
#define RIGHT 2
#define TOP 3

static const int COUNTER_CLOCKWISE = -1;
static const int CLOCKWISE = 1;
static const int ONLINE_BACK = 2;
static const int ONLINE_FRONT = -2;
static const int ON_SEGMENT = 0;

double add(double a,double b) {
    if (abs(a + b) < EPS*(abs(a) + abs(b)))return 0;
    return a + b;
}

class point {
public:
    double x, y;
    point(double x = 0, double y = 0) :x(x), y(y) {}
    point operator +(point p) { return point(x+p.x, y+p.y); }
    point operator -(point p) { return point(x - p.x,y - p.y); }
    point operator *(double a) { return point(a*x, a*y); }
    point operator /(double a) { return point(x / a, y / a); }
    double norm() { return x*x + y*y; }
    double abs() { return sqrt(norm()); }
    bool operator<(const point&p)const {
        return x != p.x ? x < p.x : y < p.y;
    }
    bool operator ==(const point&p)const {
        return x == p.x && y == p.y;
    }
    double dot(point p) {
        return x*p.x+y*p.y;
    }
    double det(point p) {
        return x*p.y- y*p.x;
    }
};

struct Segment {
    point p1, p2;
    Segment(point p1 = point(), point p2 = point()) :p1(p1), p2(p2) {}
};
typedef Segment line;

typedef vector<point>Polygon;
//????????????p0p1?????????p0p2????????¬??????
int ccw(point p0, point p1, point p2) {
    point a = p1 - p0;
    point b = p2 - p0;
    if (a.det(b) > EPS)return COUNTER_CLOCKWISE;
    if (a.det(b) < -EPS)return CLOCKWISE;
    if (a.dot(b) < -EPS)return ONLINE_BACK;
    if (a.norm() >= b.norm())return ON_SEGMENT;//!!
    return ONLINE_FRONT;
}
//????????????p1p2???p3p4????????????
bool intersect(point p1, point p2, point p3, point p4) {
    return (ccw(p1, p2, p3)*ccw(p1, p2, p4) < 0 &&
        ccw(p3, p4, p1)*ccw(p3, p4, p2) < 0);//!!!!!!!!!!!!!!!!!!!!!!!!!!!
}


inline double normalize(double r)
{
    if (r < -pi / 2.0 + EPS) r += pi * 2;
    return r;
}

double arg(const point& p) { return normalize(atan2(p.y, p.x)); }
inline bool double_cmp(double a,double b) {
    return a + EPS < b;
}


////
typedef vector<point>Polygon;



vector<point> convex_hull(point *ps, int N)
{
    sort(ps, ps + N);
    int k = 0;   // 凸包的顶点数
    vector<point> qs(N * 2);   // 构造中的凸包
                           // 构造凸包的下侧
    for (int i = 0; i < N; ++i)
    {
        while (k > 1 && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
        qs[k++] = ps[i];
    }
    // 构造凸包的上侧
    for (int i = N - 2, t = k; i >= 0; --i)
    {
        while (k > t && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k;
        qs[k++] = ps[i];
    }
    qs.resize(k - 1);
    return qs;
}

point s[N_MAX];
int n;
double a[N_MAX];//记录凸包每条边行成的向量倾斜度
int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%lf%lf", &s[i].x, &s[i].y);  
    }
    int N;
    Polygon con;
    if (n > 1) { 
        
         con=convex_hull(s,n);
        N = con.size();
        con.push_back(con[0]);
    }
        for (int i = 0; i <N; i++) {
            a[i] = arg(con[i + 1] - con[i]);
        }
    
    sort(a, a + N, double_cmp);
    point p1, p2;
    while (scanf("%lf%lf%lf%lf",&p1.x,&p1.y,&p2.x,&p2.y)!=EOF) {
        if (n < 2) { puts("GOOD"); continue; }
        int i = upper_bound(a, a + N, arg(p2 - p1), double_cmp) - a;
        int j = upper_bound(a, a + N, arg(p1 - p2), double_cmp) - a;
        puts((((p2 - p1).det(con[i] - p1) * (p2 - p1).det(con[j] - p1) > -EPS)) ? "GOOD" : "BAD");
    
    }

    return 0;
}