poj 3293 Rectilinear polygon
Rectilinear polygon
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 2125 | Accepted: 249 |
Description
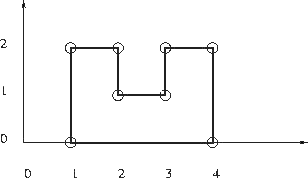Given is n points with integer coordinates in the plane. Is it is possible to construct a simple, that is non-intersecting, rectilinear polygon with the given points as vertices? In a rectilinear polygon there are at least 4 vertices and every edge is either horizontal or vertical; each vertex is an endpoint of exactly one horizontal edge and one vertical edge. There are no holes in a polygon.
Input
The first line of input is an integer giving the number of cases that follow. The input of each case starts with an integer 4 ≤ n ≤ 100000 giving the number of points for this test case. It is followed by n pairs of integers specifying the x and y coordinates of the points for this case.
Output
The output should contain one line for each case on input. Each line should contain one integer number giving the length of the rectilinear polygon passing throught the given points when it exists; otherwise, it should contain -1.
Sample Input
1 8 1 2 1 0 2 1 2 2 3 2 3 1 4 0 4 2
Sample Output
12
题意：平面图上给出一些点的坐标，通过这些点希望构成一类多边形，多边形中间没有洞，并且每个点是且仅是该多边形的一条横边和一条竖边的端点，且横边竖边不相交(横竖边共用一个端点的情况除外)，若给出的那些点能构成符合要求的多边形，
那么计算多边形的周长，否则输出-1.
思路：平面扫描，按照x轴扫描可以获得所有竖边的长度和，按y轴的同理，先讨论x轴的情况，将点按照x坐标大小排序后，同一列上的点按照y坐标从小到大排序，之后再观察多边形每一列的特性，可以发现每一列上点必定偶数个，相邻两个配对可以成为一条边，若出现奇数条边，肯定是构不成多边形的。按y轴扫描
也是相同做法。其次还要判断是否有横竖边相交的情况以及是否有洞(图是否连通)即可。
AC代码：
#define _CRT_SECURE_NO_DEPRECATE #include<iostream> #include<stdio.h> #include<algorithm> #include<queue> #include<set> #include<vector> #include<cstring> #include<string> #include<functional> #include<cmath> #include<stack> using namespace std; const int N_MAX = 100000 + 5; #define INF 0x3f3f3f3f #define EPS 1e-10 #define equals(a,b) (fabs(a-b)<EPS) static const int COUNTER_CLOCKWISE = -1; static const int CLOCKWISE = 1; static const int ONLINE_BACK = 2; static const int ONLINE_FRONT = -2; static const int ON_SEGMENT = 0; int n;//点的数量 int link_x[N_MAX], link_y[N_MAX]; class point { public: int x, y; int id; point(int x = 0, int y = 0, int id = 0) :x(x), y(y), id(id) {} int get(const bool& is_x) {//用于双向扫描 return is_x ? x : y; } void link(const point& b, const bool& is_x) {//当前点与点b相连,!!!!不是必须 (is_x ? link_x[id] : link_y[id]) = b.id; (is_x ? link_x[b.id] : link_y[b.id]) = id; } int get_link(const bool &is_x) { return is_x ? link_x[id] : link_y[id]; } point operator +(point p) { return point(x + p.x, y + p.y); } point operator -(point p) { return point(x - p.x, y - p.y); } point operator *(double a) { return point(a*x, a*y); } point operator /(double a) { return point(x / a, y / a); } double norm() { return x*x + y*y; } double abs() { return sqrt(norm()); } bool operator<(const point&p)const { return x != p.x ? x < p.x : y < p.y; } bool operator ==(const point&p)const { return x == p.x && y == p.y; } double dot(point p) { return x*p.x + y*p.y; } double det(point p) { return x*p.y - y*p.x; } }P[N_MAX]; bool is_x; bool cmp( point a, point b) { int ax = a.get(is_x); int ay = a.get(!is_x); int bx = b.get(is_x); int by = b.get(!is_x); if (ax != bx) { return ax < bx; } else return ay < by; } typedef point Vector; struct Segment { point p1, p2; Segment(point p1 = point(), point p2 = point()) :p1(p1), p2(p2) {} }; //vector<Segment>S_x; Segment S_x[N_MAX]; typedef Segment line; class Circle { public: point c; double r; Circle(point c = point(), double r = 0.0) :c(c), r(r) {} }; typedef vector<point>Polygon; //p在线段s上的投影 point project(Segment s, point p) { Vector base = s.p2 - s.p1; double r = base.dot(p - s.p1) / base.norm(); return s.p1 + base*r; } //点p关于直线s的对称点 point reflect(Segment s, point p) { return p + (project(s, p) - p)*2.0; } //点与点间距离 double getDistance(point a, point b) { return (a - b).abs(); } //点到直线距离 double getDistanceLP(line l, point p) { return fabs((l.p1 - l.p2).det(p - l.p1)) / ((l.p2 - l.p1).abs()); } //点到线段的距离 double getDistanceSP(Segment s, point p) { if ((s.p2 - s.p1).dot(p - s.p1) < 0.0)return (p - s.p1).abs(); if ((s.p1 - s.p2).dot(p - s.p2) < 0.0)return (p - s.p2).abs();//!!!!! return getDistanceLP(s, p); } //判断线段p0p1与线段p0p2的旋转关系 int ccw(point p0, point p1, point p2) { Vector a = p1 - p0; Vector b = p2 - p0; if (a.det(b) > EPS)return COUNTER_CLOCKWISE; if (a.det(b) < -EPS)return CLOCKWISE; if (a.dot(b) < -EPS)return ONLINE_BACK; if (a.norm() >= b.norm())return ON_SEGMENT;//!! return ONLINE_FRONT; } //判断线段p1p2与p3p4是否相交 bool intersect(point p1, point p2, point p3, point p4) { return (ccw(p1, p2, p3)*ccw(p1, p2, p4) < 0 &&//!!! ccw(p3, p4, p1)*ccw(p3, p4, p2) < 0); } //线段是否相交 bool intersect(Segment s1, Segment s2) { return intersect(s1.p1, s1.p2, s2.p1, s2.p2); } typedef vector<point>Polygon; bool judge_intersect(const Segment&a,const int&amount) { int y = a.p1.y, x1 = a.p1.x, x2 = a.p2.x; for (int i = 0; i <amount;i++) { if (y > S_x[i].p1.y&&y < S_x[i].p2.y&&x1<S_x[i].p1.x&&x2>S_x[i].p2.x) { return true; } } return false; } int traverse(int&amount) {//返回总长度，不符条件-1 sort(P, P + n, cmp);//!!!!每次扫描前先排序 int count = 1, sum = 0; for (int i = 1; i < n; i++) {//遍历每一个点 if (P[i].get(is_x)!=P[i - 1].get(is_x)) {//到了新的扫描层 if (count & 1)return -1; count = 1; } else { count++; if (!(count & 1)) { sum += P[i].get(!is_x) - P[i - 1].get(!is_x); P[i].link(P[i - 1], is_x); if (is_x) {//若是横向扫描，直接记录连接好的线段 S_x[amount++]=Segment(P[i-1], P[i]); } else {//竖向扫描，判断当前连接线段是否和上面的记录的线段相交 if (judge_intersect(Segment(P[i-1],P[i]),amount)) { return -1; } } } } } return sum; } int solve() { int amount = 0;//记录连边的个数 is_x=1; int num_x = traverse(amount); if (num_x == -1)return -1;//!!!! is_x =0; int num_y = traverse(amount); if (num_y == -1)return -1; int loop = 0,count=0; do {//判断不联通的图 loop = is_x ? link_x[loop] : link_y[loop]; count++; is_x = !is_x; } while (loop != 0); if (count != n)return -1; return num_x + num_y; } int main() { int t; scanf("%d", &t); while (t--) { scanf("%d", &n); for (int i = 0; i < n; i++) { int x, y; scanf("%d%d", &x, &y); P[i] = point(x, y, i); } printf("%d\n",solve()); } return 0; }
