回文串和回文自动机
https://www.luogu.com.cn/blog/PinkRabbit/PAMViz
1 PAM 简介
1.1 PAM 的形式
PAM 是一个自动机,它的普通边组成了两棵树,fail 边组成了一棵树。
这两棵普通树分别表示主串中所有奇数长度的回文串和偶数长度的回文串,其根节点分别叫做“奇根”和“偶根”。普通边上有字母(类似 trie/SAM 的普通边,都是存 \(\sum\) 个外链,但是有一些是无效的)。一个节点代表一个回文串:考虑从其到所在根的路径上字母拼起来为 \(s_1s_2...s_k\),那么如果这个节点在奇树上那么其表示 \(s_1s_2...s_{k-1}s_ks_{k-1}...s_2s_1\),否则表示 \(s_1s_2...s_{k-1}s_ks_ks_{k-1}...s_2s_1\)。
由上所述一个节点表示一个良定义的串,那么其 fail 边表示代表其最长回文后缀的节点。
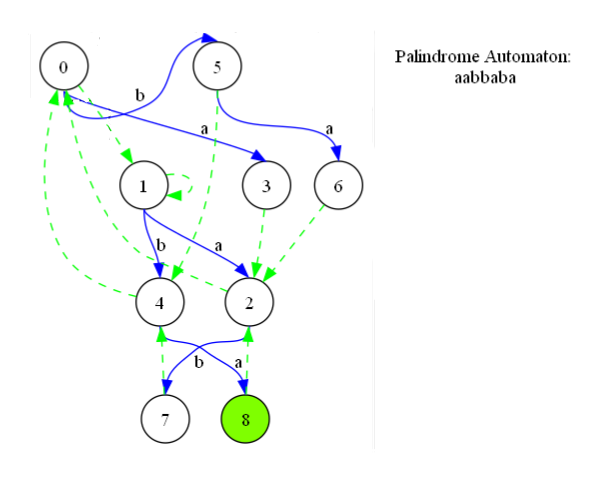
1.2 PAM 的构建
考虑增量构造法。令 \(lst\) 为目前加入的字符串的最长回文后缀所在节点。现在在字符串背后插入 \(x\) 字符,假设插入完这个字符之后有 \(n\) 个字符。我们维护每一个节点表示的字符串长度 \(len\)。考虑从 \(lst\) 开始不断跳 \(fail\),直到 \(s_n = s_{n - len_{lst} - 1}\),也就是从 \(lst\) 开始可以往左右分别加入一个字符为止,此时新的字符串的最长回文后缀就是 \(lst\) 的 \(x\) 普通边,如果不存在则需要新建。
我们记找到的这个点为 \(now\)。考虑继续从 \(fa_{lst}\) 向上跳 \(fa\) 直到 \(s_n = s_{n-len_{lst} - 1}\)。此时找到了 \(fail_{now}\)。关键的性质来了:这时候 \(fail_{now}\) 一定存在,从而也不需要继续往下找到它的最长回文后缀了。
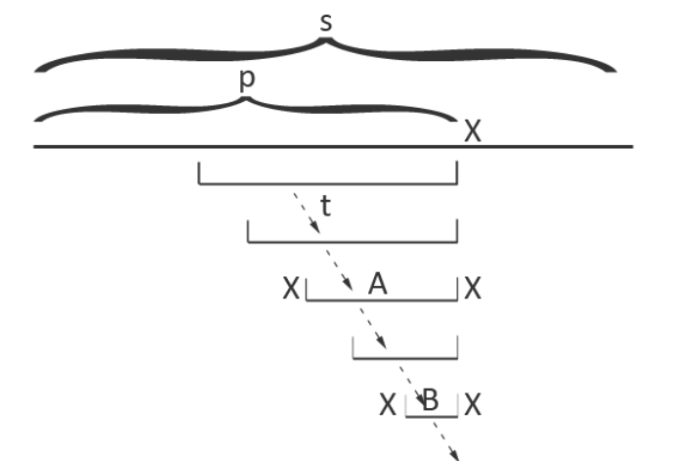
引理 1:\(fail_{now}\) 一定存在。
引理 2:回文自动机上一定出现了所有回文串。
考虑归纳证明这两个引理的正确性。
首先我们假设上一步结束之后满足条件。
考虑引理 2 的正确性:只需要满足所有后缀回文串会在这一步内添加到 PAM。
如果引理 1 成立,那么加入最大的那个后缀回文串之后,次大的一定之前就在 PAM 中,那么引理 2 就是正确的了。
考虑引理 1:首先次大的这个串 \(xBx\) 一定在之前出现过。由于 \(xAx\) 是回文串,所以 \(xAx\) 的前 \(len_B + 2\) 个字符一定是 \(xBx\),所以在之前就已经出现过了。其次由于归纳假设,已经出现过的串在 PAM 上。因此引理 1 成立。
从而我们证明了这两个引理。
接下来考虑奇根和偶根的参数应当怎么设置。我习惯令 \(0\) 号节点为偶根,\(1\) 号节点为奇根。由于我们希望奇根不会失配,令其 \(len = -1\) 即可。而偶根的 \(len = 0\)。接下来我们考虑如何设置他们的 fail 指针,以及正常节点一直向上跳应该跳到哪里。
这里结合一个例子来讲。考虑串 \(\mathtt {aaaaba(a)}\)。增加最后一个 \(\mathtt a\) 的时候 \(lst\) 的 \(len = 3\),也即 \(\mathtt {aba}\)。我们接下来要跳 fail 是因为要找到一个两边都能接的上 \(\mathtt a\) 的点。在这个串里,这个点恰恰是偶根。所以我们是要在正常的回文后缀之后增加奇根和偶根作为前面全部不符合条件的备选项,而先选择偶根然后才选择奇根。因此应该令 \(fail_0 = 1\),且正常节点的 \(fail\) 如果未定义的话应该为 \(0\)。
如何令这个想法兼容我们的算法流程?考虑 \(0\) 应该是某一个点的 \(x\) 边。考虑这个串里面 \(fail_{now}\) 是如何求出。它的普通父亲是 \(0\),当我们跳到 \(-1\) 的时候匹配上,这时候 \(fail_{now} = edge_{1, x}\)。如果 \(edge_{1, x}\) 有值,那么 \(fail_{now}\) 应当是这个值。否则 \(fail_{now}\) 应当是 \(0\)。因此只需要令 \(edge_{1, *}\) 初始全为 \(0\) 即可。
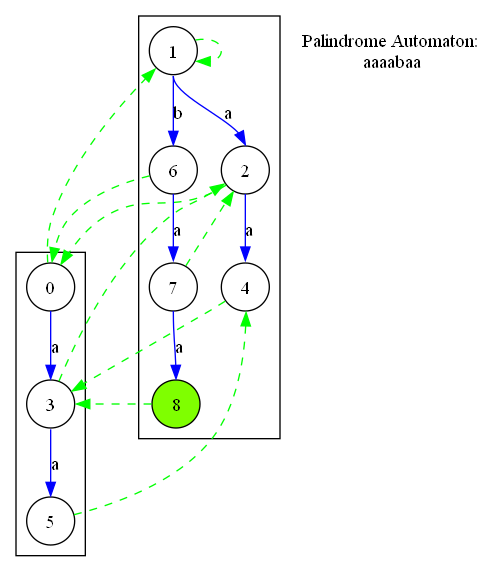
(如上图,\(\mathtt {aa}\) 的 \(fail\) 应当为 \(\mathtt a\),因为 \(edge_{1, a} = \mathtt a\);如果没有值,那么应该为 \(0\))
由此可见,\(fail_1\) 也应当设置为 \(1\)。
cnt = 1; lst = 1; n = 0; fail[0] = fail[1] = 1; len[0] = 0; len[1] = -1;
1.3 PAM 的正确性
性质 1:PAM 的状态数线性。
由于上一步证明了一次只会增加至多一个节点,所以显然线性状态数成立。
这个性质等价于,一个字符串的本质不同回文串个数等于其字符数。
对于空间:你只需要开 \(n + O(1)\) 个节点即可,不同于 SAM 的 \(2n +O(1)\)。
性质 2:PAM 的跳转次数为线性。
首先除了跳 fail 之外的操作显然为 \(O(n)\)。那么只需要考虑跳 fail 操作的次数即可。
跳 fail 分两步:第一步是从 \(lst\) 开始跳 fail 直到找到普通树上 \(now\) 的父亲。第二步是从 \(now\) 的父亲的 fail 开始跳 fail 直到找到 \(fail_{now}\) 的父亲。
考虑第一步的跳转次数。我们发现下一次的起点就是上一次的终点的普通儿子,儿子关系深度最多增加 \(1\),跳一次深度减少 \(1\),所以跳转次数为 \(O(n)\)。
考虑第二步的跳转次数。
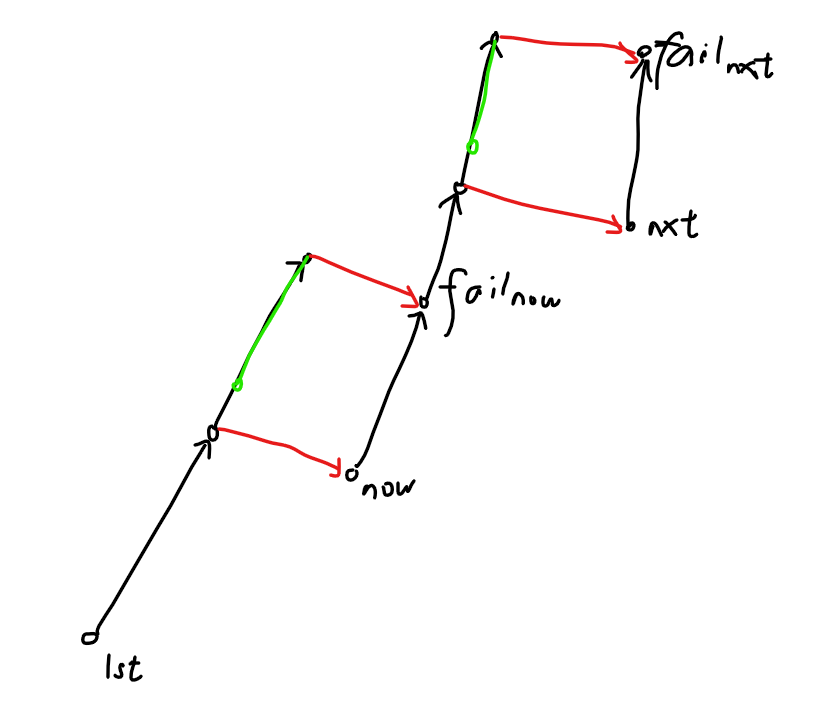
如上图,红边是一个普通边,黑边是若干个 fail 边。绿色是第二步跳转的路径。可以直观地看出,下一次跳转的起点比上一次跳转的终点的深度更低。所以跳转次数也为 \(O(n)\)。
1.4 PAM 的运用
运用 1:求本质不同回文子串个数。
就是状态数减去奇根和偶根两个状态。
运用 2:求回文子串出现次数。
考虑某一个前缀。我们知道其最长回文后缀所在的节点,并且它如果出现了,那么它的所有 fail 祖先也会出现一次。因此我们只需要对增量构造的时候走到每一个 \(now\) 的时候对 \(dp_{now}\) 增加 \(1\),然后某一个回文子串的出现次数就是其子树 \(dp\) 值的和。
这个做法的关键在于出现的所有回文串组成 fail 树上的一条链。这也可以套用到其他的应用上。
1.5 PAM 和 manacher 的运用场景对比
OI-wiki 上有一句话,“由于空间限制,PAM 不能完全替代 manacher。”也就是说,除了空间限制之外,PAM 完全可以替代 manacher?
回顾一下,manacher 求出了以每一个点为回文中心的时候,最长回文半径是什么。所有回文串可以被分成 \(2n\) 类,其中每一类的回文中心一致,并且回文半径连续。而 PAM 也隐式维护了每个回文子串的所有出现位置集合,可以认为两者等效。
而 manacher 很难求本质不同回文串为单位的信息,用上弱周期引理的话可以做到单 \(\log\),但是 PAM 可以轻松做到线性;和 SAM 一样,知道本质不同回文串为单位的信息之后你就可以乘以它的出现次数。
因此,PAM 确实可以完全替代 manacher。
P5496【模板】回文自动机
给定一个字符串,求每一个位置结尾的回文子串个数。
答案即为 \(now\) 在 \(fail\) 树上的深度,其中认为 \(dep_0 = dep_1 = 0\)。
写的时候注意一下 \(now\) 和 \(lst\) 不是一个东西。
string s;
struct PAM {
int cnt, lst, fail[500010], ed[500010][26], len[500010], occ[500010], n;
vector<int> t[500100]; int dep[500010];
PAM() {
memset(occ, 0, sizeof(occ));
memset(fail, 0, sizeof(fail));
memset(ed, 0, sizeof(ed));
memset(len, 0, sizeof(len));
memset(dep, 0, sizeof(dep));
cnt = 1; lst = 0; n = 0; fail[0] = fail[1] = 1; len[0] = 0; len[1] = -1;
}
int getfa(int x) {
while(s[n] != s[n - len[x] - 1]) x = fail[x];
return x;
}
int insert(char x) {
n++;
int p = getfa(lst);
if(!ed[p][x - 'a']) {
++cnt; len[cnt] = len[p] + 2;
int np = getfa(fail[p]);
fail[cnt] = ed[np][x - 'a']; dep[cnt] = dep[fail[cnt]] + 1;
ed[p][x - 'a'] = cnt;
}
occ[ed[p][x - 'a']] ++; lst = ed[p][x - 'a'];
cout << dep[lst] << " \n"[n==(int)s.size()-1];
return dep[lst];
}
}pam;
signed main() {
cin >> s; int k = 0; s = ' ' + s;
for(char &ch : s) {
if(ch == ' ') continue;
ch = (ch - 97 + k) % 26 + 97;
k = pam.insert(ch);
}
}
CF1827C Palindrome Partition
给定字符串 \(s\),求有多少它的子串(连续)使得它是一个偶长度回文串或者若干个偶长度回文串的拼接。两个子串不同当且仅当它们在原串里位置不同。
\(\sum |s| \le 5 \times 10^5\)
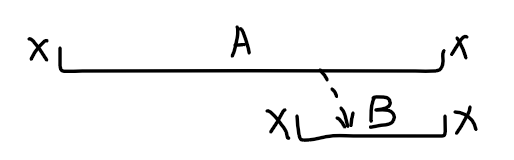
想到 \(dp_i\) 表示以 \(i\) 结尾的符合条件串的个数,用偶回文串转移。但是这是一条 fail 树上链上散点的 \(i-j\) 型转移,不可做。
突然发现,如果这样转移会算重,也就是存在不同的划分方式。但是如果选择一个最小的划分,也即取 fail 树上 \(len\) 最小的偶数回文串进行转移,貌似不会算重/漏!
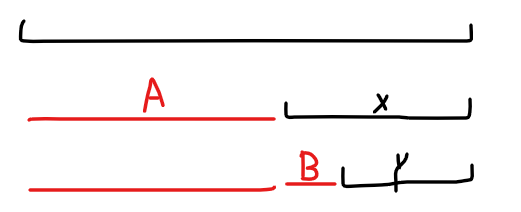
如上图:如果一个偶回文拼接可以由一个偶回文拼接 \(A\) 和一个偶回文串 \(X\) 组成,并且 \(Y\) 是回文串,那么 \(B\) 一定是偶回文拼接,于是 \(A+B\) 也是偶回文拼接,所以 \(Y\) 也是一个方案。
这样的话只需要维护最小长度的偶数回文后缀,即可转移。
初学者经常有的一个 typo 是 \(cnt\) 和 \(lst\) 的问题,写挂两次了,下次要先看看是不是这里挂了。
void insert(char ch) {
++n; int p = getfa(lst);
if(!ed[p][ch - 'a']) {
++cnt; int np = getfa(fail[p]); len[cnt] = len[p] + 2;
fail[cnt] = ed[np][ch - 'a']; ed[p][ch - 'a'] = cnt;
if(len[cnt] % 2 == 0 && mxlen[fail[cnt]] & 1) mxlen[cnt] = len[cnt];
else mxlen[cnt] = mxlen[fail[cnt]];
}
lst = ed[p][ch - 'a'];
if(mxlen[lst] % 2 == 0) dp[n] = dp[n - mxlen[lst]] + 1;
}
还有清空的时候不要重新写一个构造函数,就直接在原来的 pam 上面清空,会保留之前的 \(cnt,n\) 数据。
void init() {
f(i, 0, cnt) {fail[i] = len[i] = mxlen[i] = 0; f(j, 0, 25) ed[i][j] = 0; }
f(i, 1, n) dp[i] = 0;
cnt = 1; lst = 1; fail[0] = fail[1] = 1; len[1] = -1; n = 0; len[0] = 0;
mxlen[1] = mxlen[0] = -1;
}
2 回文串和周期
回文串的周期性质是一个很重要的考点。先回顾一下周期相关性质。
定理 1:一个串 \(s\) 有 border \(t\),那么有周期 \(|s| - |t|\)。
有 border \(t\) 意味着对于 \(i \le |t|, s_i = s_{|s| - |t| + i}\);有周期 \(x\) 意味着对于 \(i \le |s|-x, s_i = s_{i+x}\)。令 \(x = |s|-|t|\),显然两者等价。
定理 2:(周期引理)一个串 \(s\) 如果有周期 \(x, y\),\(x+y \le n + \gcd(x, y)\),那么 \(\gcd(x,y)\) 也是周期。
这个定理能证,但是不是非常 trivial,记住结论就好了,证明不重要。
定理 3:串 \(s\) 在 \((x, 2x]\) 中的所有 border 构成等差数列。
考虑这个区间内的最长的 border。将它们合并是不改变比它们短的 border 的。合并之后有新的 border-周期对应关系,而任意两个周期之和都不超过 \(2x\)。
再往下就是很深刻的性质了,往基本子串字典方向走了。
但是对于回文串有非常重要的性质:
定理 4:一个回文串 \(S\) 的所有 border 一定是回文串。
这是因为 \(pre_i S = suf_i S = rev(suf_i S)\),那么其一定是回文串。
定理 5:一个回文串的所有回文后缀都是 border。
显然有 \(pre_iS = rev(suf_i S) = suf_i S\)。
定理 6:一个回文串的最大 border 是其最大回文后缀。
由定理 4 和定理 5 显然可得。
ucup1H. P-P-Palindrome
给定 \(n\) 个字符串 \(S_1, ..., S_n\),
一个 \(\mathtt{P-P-Palindrome}\) 定义为一个有序对 \((P, Q)\),其中 \(P, Q\) 都是 \(S_1, ..., S_n\) 中某一个字符串的子串,并且 \(P,Q,P+Q\) 都是回文串。
计算不同的 \(\mathtt{P-P-Palindrome}\) 个数,其中两个 \(\mathtt{P-P-Palindrome}\) 不同当且仅当 \(P\) 不同或者 \(Q\) 不同。
\(1 \le n \le 10^6, 1 \le \sum |S_i| \le 10^6\)
这题引入了一个很深刻的性质 1:如果 \(P\) 和 \(Q\) 和 \(P+Q\) 都是回文串,那么他们有相同的最小整周期。
证明:\(|P|\) 是 \(P+Q\) 的周期,\(|Q|\) 也是 \(P+Q\) 的周期,由周期引理 \(\gcd(|P|,|Q|)\) 是 \(P+Q\) 的周期,显然它也是 \(P\) 的整周期,也是 \(P+Q\) 的整周期。
进一步地,这两个整周期的内容一定也相同,因此它们的最小整周期也相同!那么,如果 \(P\) 和 \(Q\) 能够组成 P-P-Palindrome 那么 \(P\) 和 \(Q\) 的最小整周期一定相同!
考虑我们在 PAM 上维护了什么。如果一个点连向 \(0\),那么它没有真 border,也就是说最小周期是自己;否则,最小周期是自己去除连向的那个点。
这时候我们大概知道可以对 PAM 的每一个节点(本质不同回文串个数 \(O(n)\))求出其最小整周期,然后放进等价类中,一个等价类的贡献就是其大小的平方。
但是还有一个问题,就是一个字符串的最小整周期不一定是最小周期!而如果两个回文串的最小整周期相同那么可以推出它们可以组成 P-P-Palindrome,但是如果两个回文串的最小周期相同就不一定了,举个例子:aba 的一个周期是 \(2\),而 aba + abababa 并不是一个回文串。(这个样例可以得到错误,也可以对拍出来,但是最好的方法依然是真正推出来发现没有任何死角)
所以我们只能找每一个回文串的最小整周期。那么怎么找呢?
性质 2:如果一个回文串有整 border(也就是有不等于自身的整周期),那么最小整周期一定是最小周期。
这是个非常深刻的性质,考虑回文串形如 SSSS,S 是最小整周期。如果存在 TSSS 也是回文串,那么你会发现对不准(形式化的 \(S_i = S_{(i + |T|) \% |S|}\) 需要成立)但是这是不可能的。
也就是说,如果一个回文串有整周期,我们可以从 PAM 上得到;如果 PAM 上的儿子并不是整 border,那么这个回文串没有整周期(也就是说最小整周期是自己)。
所以我们确实可以从 PAM 上找到父亲,判断父亲是否是整 border,再将其归类到其最小整周期的等价类。
这个归类过程可以使用字符串哈希,注意千万不要用自然溢出,然后满足生日悖论即可。自然溢出会 wa on 15,哈哈。
注意 PAM 不要写挂了。
map<array<int, 3>, int> mp;
int base[3] = {114514, 191981, 202009}, mod[3] = {1145141979, 998244353, 1000000007};
int powp[3][1000010];
struct PAM {
int cnt, lst, n; string s; int tot;
vector<int> fail; vector<array<int, 26>> ed; vector<int> len; vector<int> pre[3];
PAM() {
cnt = 1; lst = 1; n = 0; fail.push_back(1); fail.push_back(1);
ed.push_back({0}); ed.push_back({0}); len.push_back(0);
len.push_back(-1); f(_, 0, 2) pre[_].push_back(0);
tot = 0;
}
int getfa(int x) {
while(s[n] != s[n - len[x] - 1]) x = fail[x];
return x;
}
array<int, 3> hx(int l, int r) {
array<int, 3> ret;
f(i, 0, 2) ret[i] = (pre[i][r] - pre[i][l - 1] * powp[i][r - l + 1] % mod[i] + mod[i]) % mod[i];
return ret;
}
void input(int l, int leng) {
int r = l + leng - 1;
array<int, 3> tt = hx(l, r);
if(mp.count(tt)) mp[tt] ++; else mp[tt] = 1;
}
void insert(char ch) {
n++; int p = getfa(lst);
f(_, 0, 2) pre[_].push_back(((pre[_][n-1] * base[_]) + s[n]) % mod[_]);
if(!ed[p][ch - 'a']) {
++cnt; fail.push_back(0); ed.push_back({0}); len.push_back(len[p]+2);
int np = getfa(fail[p]); fail[cnt] = ed[np][ch - 'a'];
ed[p][ch - 'a'] = cnt;
if(len[cnt] % (len[cnt] - len[fail[cnt]]) == 0) {
input(n - len[cnt] + 1, len[cnt] - len[fail[cnt]]);
}
else {
input(n - len[cnt] + 1, len[cnt]);
}
}
lst = ed[p][ch - 'a'];
}
}pam;
signed main() {
int n; cin >> n;
f(_, 0, 2) powp[_][0] = 1;
f(_, 0, 2) for(int i = 1; i <= 1000000; i ++) powp[_][i] = powp[_][i - 1] * base[_] % mod[_];
f(i, 1, n) {
pam.lst = 1; pam.n = 0; f(_, 0, 2) {pam.pre[_].clear(); pam.pre[_].push_back(0); }
cin >> pam.s; pam.s = ' ' + pam.s;
for(char ch : pam.s) if(ch != ' ') pam.insert(ch);
}
int ans = 0;
for(auto it : mp) {
ans += it.second * it.second;
}
cout << ans << endl;
};
【要点总结】
- 双回文串的深刻性质。
- 严谨的关于周期的推导和分类讨论。


