有向图 dp
1.1 什么是有向图 dp
我们遇到的博弈问题,例如【省选联考 2023】过河卒,很多都是转化为有向图博弈,其形如:一些节点为终止节点,状态已经确定;一个点的状态由其出边所到达点的状态确定。
如果是 DAG 上,显然我们可以按照拓扑序让每个点搜索到的时候其所有出边都已经确定了状态。但是题目有时候并不是这么温柔。出现了环的时候题目就变得困难了。
对于一般情况的这种 dp,不弱于解丢番图方程,所以一般来说都有一些 adhoc 的策略在里面,但是也是有迹可循,稍微有那么一点套路的。
拓扑排序可以帮你找到环,并依然可以对能确定的状态找到答案;但如果某个点的答案可以“抛弃环上点”(并不是必须所有出边都确定),那么有可能需要使用 dijkstra 等额外工具。
CF325C. Monsters and Diamonds
【题意】
有 \(n\) 种普通材料和 \(m\) 种变换规则。普通材料编号从 \(1\) 到 \(n\),此外还有一种编号为 \(-1\) 的特殊材料。
每种变换规则均形如,消耗一份普通材料 \(x_i\),获得材料 \(p_{i,1}\dots p_{i,k_i}\) 各一份。
保证对于编号 \(1\dots n\) 的每种材料至少有一个变换规则消耗该材料,保证每种变换规则至少产生一份特殊材料。
对于每种普通材料,你需要求出,若初始时恰有一份该材料,一直进行变换直至无法变换时,最少和最多各可获得多少特殊材料。
输出规则如下:
- 若无论如何,变换均无法停止,该行输出
-1 -1。 - 若你可以停止变换,同时获得无限多的特殊材料,则该行最大值的位置输出
-2。 - 若不满足以上两点,则你输出的答案对 \(314000000\) 取 \(\min\)。
\(n,m,\sum k_i\le 10^5\)。
【分析】
考虑对每一种变换方式建立虚点,如下图:
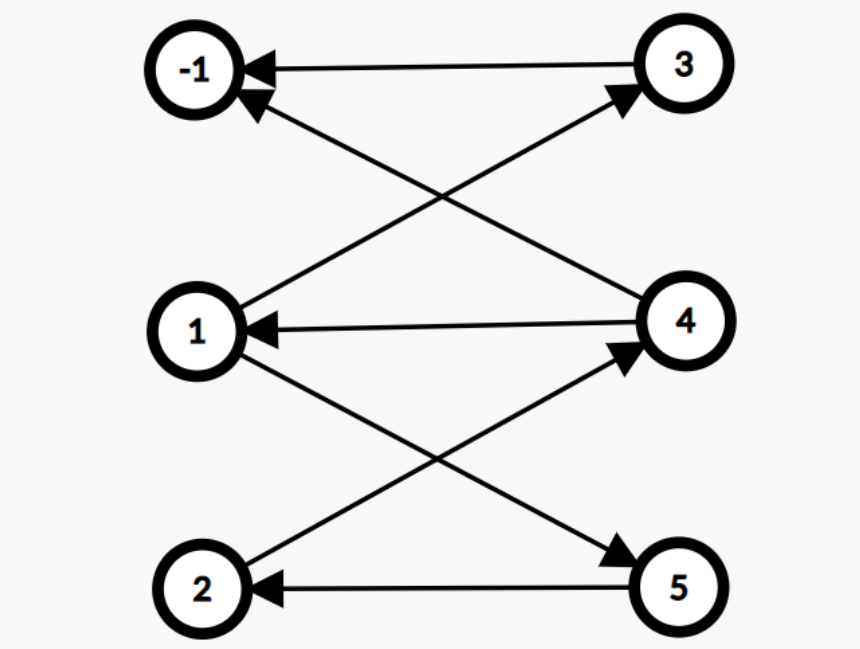
我们尝试先解决 \(\min, \max\) 其中一个问题。
我们应当选择 \(\min\) 问题,因为如果它的答案只有两种,然后求出来之后可以得到 \(-1\),这样 \(\max\) 问题答案也只剩下两种。
考虑 \(\min\) 问题。令 \(dp_i\) 表示 \(1\) 个 \(i\) 物品能换到最少的 \(-1\) 是几个。要么有值,要么 \(-1\)。其中 \(dp_{-1} = 1\),其实这个点没用。
把 \(1 \sim n\) 叫做左部点,\(n + 1 \sim n + m\) 叫做右部点,那么左部点的答案就是所有出边状态取 \(\min\),如果某一个出边的答案一直没有确定,那么它应当是能够连向自己的,说明它的答案一定比自己的答案大,没有贡献。因此把所有能够算出来的出边进行取 \(\min\) 就是自己的答案,而右部点则是所有出边状态之和,一定要所有出边算出来才能够算出自己的。最后没有赋值到的点就是 \(-1\)。
这样的问题怎么处理?看起来有 \(\min\) 也有 \(\sum\),是个拓扑排序加上 dij。其实它用 dij 可以做。
dij 的思想是当 \(u\) 算出来的时候更新所有 \(u \sim v\) 的值,然后一个一个出队。而其需要 \(dp\) 值较大的点对较小的点没有影响。这题就满足这一个条件,如果将右部点看作是一条边,而不是一个独立点的话会更好理解。
算法就是维护一个 pq,右部点 \(deg = 0\) 的时候加入 pq,左部点只要增广到都入 pq。
什么时候用 dij?dp 方程式写出来是 \(\min\),像最短路它就是最短路。(乐)例如最小斯坦纳树的 \(dp\) 方程式写出来也是最短路。
对于 \(\max\),就好做了,把 \(-1\) 的出边入边都删掉之后,能够走到环上的点就是 \(-2\),否则就可以算出来,这个可以拓扑排序。

