wqs 二分

1.1 wqs 二分简介

现在有一个函数 $f(x)$ 是凸的，需要求出其在 $x=x_0$ 处的点值。

我们先假设它是一个下凸壳。
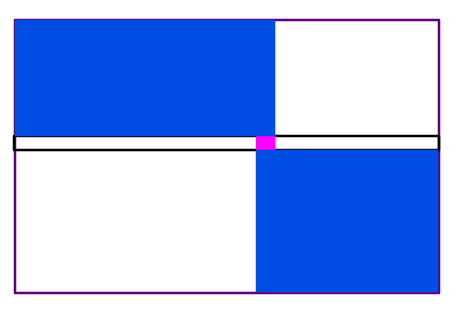
我们考虑二分斜率 $k$ ，用一条斜率为 $k$ 的直线去切这个凸包，也即求 $\min \limits_{x} f(x) - kx$ 以及取到这个点的 $x$ 。

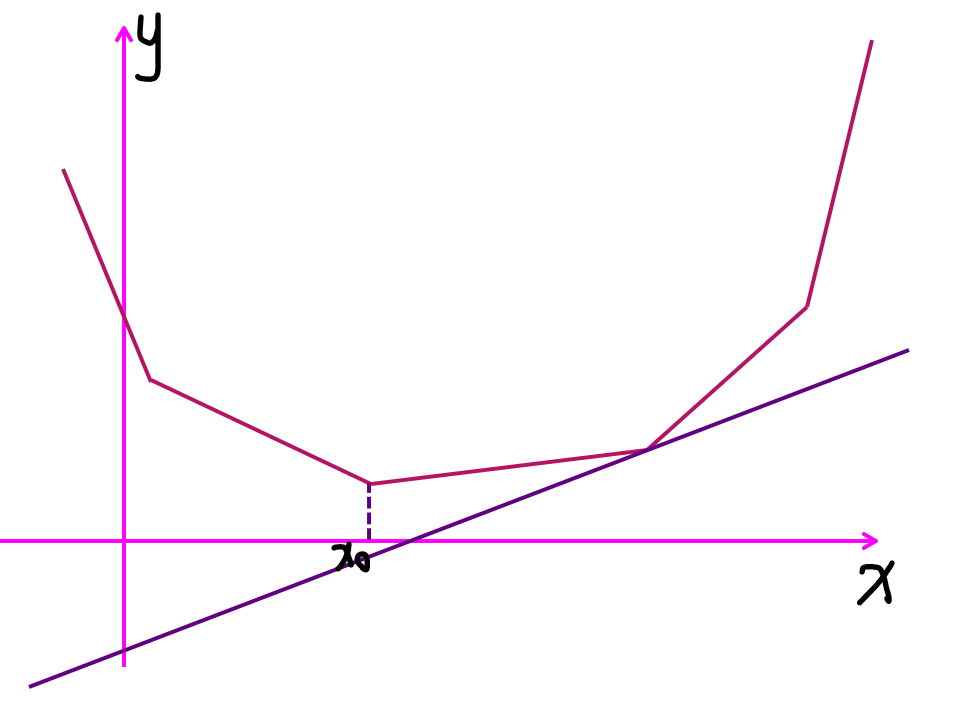
如上图，发现取到该点的 $x$ 是比 $x_0$ 大的，于是减小二分的斜率 $k$ ，直到找到 $x_0$ 。

我们把我们要求的东西变成了 $\log V$ 次 $\min \limits_{x} f(x) - kx$ 。这个式子在有些情况下比较好求：

考虑这样的问题：有 $n$ 个物品，求恰好选择 $x_0$ 个的情况下的最小代价。如果我们二分的时候将每一个物品的代价减少 $k$ ，再求一个最优解，那么就可以得到 $\min \limits_{x} f(x) - kx$ 。可能加上 $x_0$ 的限制之后不好做，但是去掉之后就很水，这时候可以用 wqs 二分。

wqs 二分就是这样的过程。在上面的问题中，凸性就是 $ans_i - ans_{i-1} \ge ans_{i+1}-ans_i$ 一定成立。这个条件满足的场景就是例如你选择两个物品，如果从 $i$ 到 $i+1$ 选择了某一个物品那么不如在 $i-1$ 到 $i$ 之间选择。

1.2 一些细节

正常情况下，如果 $f_i$ 是整数，那么 $\cfrac{f_{i} - f_{i-1}}{i-(i-1)}$ 是整数，因此二分斜率只需在整数域内二分即可。对于小数运算，可能需要在实数域内二分。实数域内二分，还是写 $100$ 次二分好一些，而不是 $l < r - 3eps$ 。后者容易死循环。

对于三点共线需要认真考虑。我们考虑这样的情形：

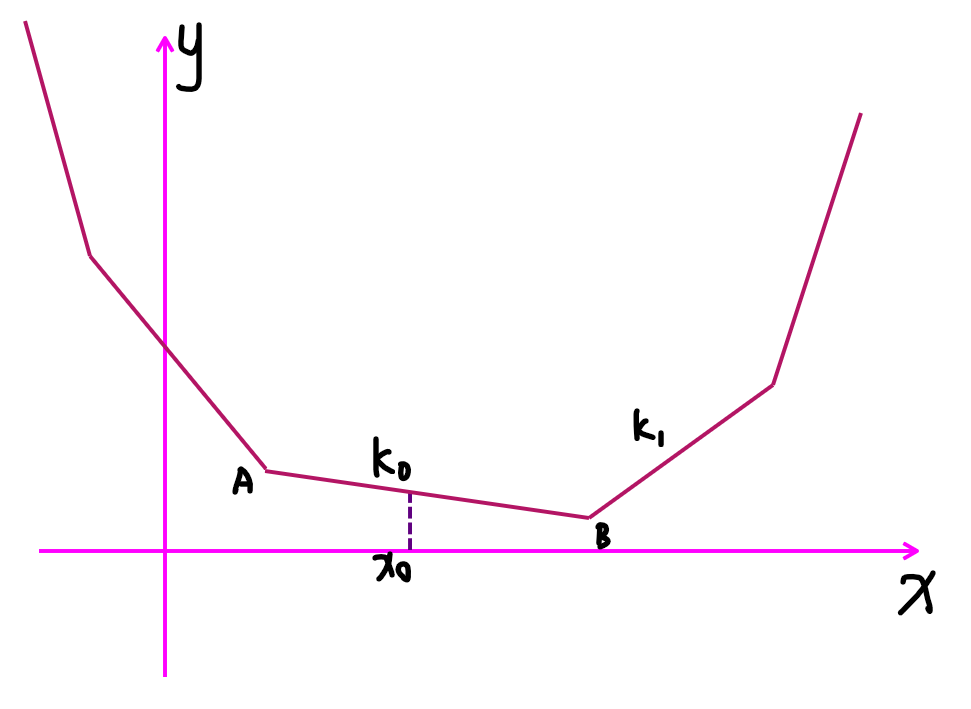
虽然我们不一定切到 $x_0$ ，但是我们一定会切到这条直线上的某一个点。这条直线都对应着唯一的截距，所以我们得到 $d, x$ 的时候只需要令答案为 $d + mid \mathbf x_0$ （就是这条直线的截距经过 $x_0$ 坐标的点）即可，而不是 $d + mid x$ 。

但是你要注意二分到实际斜率的时候程序会切到哪一个点。例如，如果我们钦定相同答案取最小个数的操作方案（也即，取最小的 $x$ 使得经过 $x$ 的某一个线段斜率为 $k$ ）那么当你二分到等于直线斜率的 $k_0$ 的时候，你会得到点 $A$ 。而你二分到的时候你会得到点。因此如果你得到的 $x \le x_0$ ，那么你需要把答案更新（赋值）为 $d + mid \mathbf x_0$ ；否则你不能更新答案。

最后，wqs 二分的条件是 $l \le r$ 而不是 $l < r$ ，否则取不到 $k_0$ 处的答案！

如果你的 dp 写挂了导致没法保证贴任何一边，还有一种方法：实数域上二分，如果 $k$ 是小数不和任何一条直线相交，那么一定会贴在某一边上。这样你可以二分到确切的 $k_0 \pm eps$ 。
一般用一个 pair 来存答案和用了几个，贴左边的话要重定义一下 cmax，但是如果你不小心写了个 max，那就寄了。

P2619 Tree I

【题意】
有一张无向图，有一些黑边和白边，要求选择一个生成树，使得恰好有 $k$ 个白边的前提下，边权和最小。

【分析】

考虑令 $ans_i$ 为有 $i$ 个白边的情况下的边权和。 $ans$ 其实是一个下凸壳。

考虑解决 $\min \limits_{x} f(x) - kx$ 的问题，其实就是给每条白边边权减去 $k$ 之后求一个最小生成树，再取其白边个数作为 $x$ 。这个是好做的。

如果我们钦定黑边比白边先选，那么就可以钦定相同答案取最小个数的操作方案。


struct edge {
    int s, t, c; 
}e[2][100010]; 
int ans; int cnt[2]; int fa[50010]; int n, m, k; 
int get(int x) {if(fa[x] == x) return x; else return fa[x] = get(fa[x]); }
void merge(int x, int y) {x = get(x); y = get(y); fa[x] = y; }
pii getans(int mid) {
    f(i, 0, n) fa[i] = i; 
    int sum = 0, dot = 0;
    for(int l = 1, r = 1; l <= cnt[0] || r <= cnt[1]; ) {
        if(l <= cnt[0] && (r > cnt[1] || e[0][l].c - mid < e[1][r].c)) {
            if(get(e[0][l].s) == get(e[0][l].t)) ;
            else { merge(e[0][l].s, e[0][l].t); sum += e[0][l].c - mid; dot++; }
            l ++; 
        }
        else {
            if(get(e[1][r].s) == get(e[1][r].t)) ;
            else {merge(e[1][r].s, e[1][r].t); sum += e[1][r].c; }
            r ++; 
        }
    }
    return {sum, dot}; 
}
signed main() {
    cin >> n >> m >> k; 
    f(i, 1, m) {
        int s, t, c, col; cin >> s >> t >> c >> col; 
        e[col][++cnt[col]] = {s, t, c};
    }
    auto cmp = [=](edge th, edge op) {return th.c < op.c; };
    f(i, 0, 1) sort(e[i] + 1, e[i] + cnt[i] + 1, cmp);
    int l = -100, r = 100; 
    while(l <= r) {
        int mid = (l + r) >> 1; 
        pii res = getans(mid); 
        int p = res.second, b = res.first;  
        if(p > k) r = mid - 1;
        else if(p == k) { ans = b + mid * k;break; }
        else {l = mid + 1;  ans = b + mid * k;}
    }
    cout << ans << endl; 
}