性质智慧题

1 性质题

1.1 寻找不变量

ucup14C LaLa and Lamp

【题意】
给定一个三角形 \(01\) 网格图，问是否能通过若干次操作将其变为全 \(0\)：选择 \(3n\) 个与三角形某一条边平行且穿过格点的边的其中一个，将其经过的所有点取反。

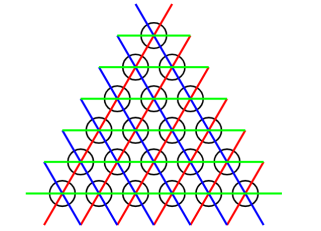
【分析】
高斯消元的元数 \(O(n)\)，条件总数 \(O(n^2)\)，显然走不通。

考虑发掘性质！发现如果只保留两条边让与它平行的边可以取反，那么每一次操作改变了一个如下菱形的其中两个点。于是若干次操作后每一个菱形的异或和都应该为 \(0\)。

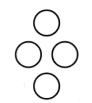
那么如果一个三角形的每一个菱形异或和都为 \(0\)，是否一定能够通过一种方式选与两条边平行的边取反，使得三角形清 \(0\) 呢？

答案是肯定的。证明如下：

首先对于一个合法的菱形，每一种都有方案使得其四个点都变成 \(0\)。那么问题就是操作间是否会有冲突呢？

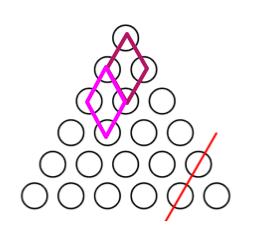
考虑消掉上面那个菱形之后，下面那个菱形只有下面的两个没有消除。这时候下面的两个要么是 \(1,1\)，要么是 \(0,0\)，这时候进行的操作对上面没有影响。

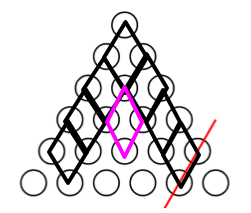
消除完黑色的所有菱形，我们发现粉色菱形已经三个点确定是 \(0\)，那么第四个点一定也是 \(0\)。以此类推，会将除了左下和右下其他的点全部确定为 \(0\)。

这两个点分别进行一次操作即可翻转。

现在回到原问题。考虑第三个方向是为了可以让为 \(1\) 的菱形改成 \(0\)。其进行一次操作会对以在它那一行的某一个点为顶/底的一个菱形取反。

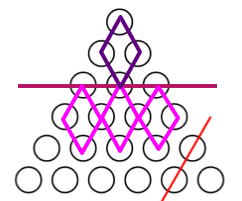
考虑从上到下判断是否操作这一行。对于第三行及以下，是否对该行进行操作是固定的，因为位于它上方的菱形只能由它取反。（如果存在状态不一样的菱形，那么直接 NO）

前两行也会影响菱形局面，但是不能马上确定。不妨直接枚举其 \(0/1\)。

时间复杂度 \(O(n^2)\)。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
char c[2020][2020]; int n; 
bool even(int x,int y){return (c[x][y]^c[x-1][y]^c[x-1][y-1]^c[x-2][y-1]) == 0;}
bool blank(int x,int y){return c[x][y]==0&&c[x-1][y]==0&&c[x-1][y-1]==0&&c[x-2][y-1]==0;}
void flip(int x,int y){return c[x][y]^=1, void();}
void modify(int x) {f(i,1,x){flip(x,i);} return;}
void judge() {f(i,3,n){int stt=even(i,2);f(j,3,i-1){if(stt!=even(i,j))return;}if(stt){modify(i);}}cout<<"YES\n";exit(0);}
signed main() {
    cin >> n; f(i,1,n)f(j,1,i){cin>>c[i][j];c[i][j]-='0';}
    judge(); modify(1); judge(); modify(2); judge(); modify(1); judge();
    cout << "NO\n";
    return 0;
}

1.2 减少分类讨论

ucup14D LaLa and Magic Stone

这题的方法是不断分讨填入方块。官方题解里面令 \((i,j)\) 为字典序最小的未填块，导致很多分讨。zky 采用的方法是找到 \(i+j\) 最小的一个块，分讨就少了很多。