纳什均衡
纳什均衡
一个游戏,\(A\) 有 \(n\) 种策略,\(B\) 有 \(m\) 种策略,两方同时出策略,当 \(A\) 出了第 \(i\) 种,\(B\) 出了第 \(j\) 种的时候,有一个结果。在这个结果集合里定义有偏序,表示某个结果在 \(A\) 看来更优/劣。
双方分别存在一个/一些策略,使得对于 \(A\) 和 \(B\) 的任何一方,如果其不改变自己的策略,那么另一个人不管如何改变策略,结果对自己不会更优。
\(A\) 的策略形如:\(\{(p_1, p_2, ..., p_n)\}, \sum p_i = 1, \forall i, p_i \in [0, 1]\),表示出 \(1,2,...,n\) 的概率分别是 \(p_1,...,p_n\)。\(B\) 同理有 \(\{(q_1, q_2, ..., q_n)\}\)。其中,如果存在 \(p_i = 1\),那么 A 一定选择出 \(i\)。
这样的策略对任何一方可能都不能达到理想情况下的最优解,但是对两个利己主义者来说,是最稳定的,是对方不管怎么选择自己都最不吃亏的一种策略。
如果纳什均衡点唯一,那么两方的策略固定,两方的期望得分固定。
例子
囚徒困境
假设有两个小偷 A 和 B 联合犯事、私入民宅被警察抓住。警方将两人分别置于不同的两个房间内进行审讯,对每一个犯罪嫌疑人,警方给出的政策是:如果一个犯罪嫌疑人坦白了罪行,交出了赃物,于是证据确凿,两人都被判有罪。如果另一个犯罪嫌疑人也作了坦白,则两人各被判刑 \(8\) 年;如果另一个犯罪嫌疑人没有坦白而是抵赖,则以妨碍公务罪(因已有证据表明其有罪)再加刑 \(2\) 年,而坦白者有功被减刑 \(8\) 年,立即释放。如果两人都抵赖,则警方因证据不足不能判两人的偷窃罪,但可以私入民宅的罪名将两人各判入狱 \(1\) 年。

关于案例,显然最好的策略是双方都抵赖,结果是大家都只被判 \(1\) 年。但是由于两人处于隔离的情况,首先应该是从心理学的角度来看,当事双方都会怀疑对方会出卖自己以求自保、其次才是亚当·斯密的理论,假设每个人都是“理性的经济人”,都会从利己的目的出发进行选择。这两个人都会有这样一个盘算过程:假如他坦白,如果我抵赖,得坐 \(10\) 年监狱,如果我坦白最多才 \(8\) 年;假如他要是抵赖,如果我也抵赖,我就会被判一年,如果我坦白就可以被释放,而他会坐 \(10\) 年牢。综合以上几种情况考虑,不管他坦白与否,对我而言都是坦白了划算。两个人都会动这样的脑筋,最终,两个人都选择了坦白,结果都被判 \(8\) 年刑期。
基于经济学中“理性的经济人”的前提假设,两个囚犯符合自己利益的选择是坦白招供,原本对双方都有利的策略不招供从而均被判处一年就不会出现。这样两人都选择坦白的策略以及因此被判 \(8\) 年的结局,纳什均衡”首先对亚当·斯密的“看不见的手”的原理提出挑战:按照斯密的理论,在市场经济中,每一个人都从利己的目的出发,而最终全社会达到利他的效果。但是我们可以从“纳什均衡”中引出“看不见的手”原理的一个悖论:从利己目的出发,结果损人不利己,既不利己也不利他。
零和博弈
定义得分:当 \(A\) 出了第 \(i\) 种,\(B\) 出了第 \(j\) 种的时候,得分为 \(M_{i,j}\),\(A\) 的目标是最大化得分,\(B\) 的目标是最小化得分,那么这是一个零和博弈。(因为 \(A\) 的得分就是 \(B\) 的得分的相反数,所以是零和的,这样可以写在一个矩阵内。如果 \(A\),\(B\) 都有得分,但是 \(A\) 目标是最大化 \(A-B\) 的得分,那么也是零和博弈)
在零和博弈中,一定存在纳什均衡,而且可以在矩阵上求出来。
定理:对矩阵 \(M_{i, j}\),每一行表示 \(A\) 选择某一个策略的所有结果;每一列是 \(B\) 选择某一个策略的所有结果。考虑 \(A\) 的均衡策略:删掉 \(B\) 不会选择的所有策略之后,对于 \(B\) 选择的每一个策略,期望得分一致的策略也就是 \(A\) 的均衡策略。
其中,不会选择的策略指:考虑每列是一个向量 \((q_1, ..., q_m)\),在 \(m\) 维空间中的凸包里(不在凸包上)的策略。
也就是一些列消掉之后,形成一个 \(n \times m'\) 的矩阵,然后对 \((p_1, ..., p_n)\) 若满足 \(C_1 = C_2 = ... = C_{m'}\),其中 \(C_i = \sum_{j} p_j M_{j, i}\),那么 \(\{p_n\}\) 是一个纳什均衡点。
这一等式显然是 \(m' - 1\) 个方程;再加上一个方程 \(p_1 + p_2 + ... + p_n = 1\),总共 \(m'\) 个方程,一定有解(证明比较复杂,运用到 Kakutani 不定点定理,略去),取其中的所有非负整数解即是所有纳什均衡点。(如果有很多解,可能要上线性规划)
做 \(m\) 维凸包是困难的。但是有的题目并没有哪个 \(B\) 的策略没用,可以这样判断:
直接对矩阵做高斯消元,得出来如果是唯一解,或者是解的每一维都是非负数,那么是纳什均衡。不然的话有凸包内的点要去掉。
P9142 [THUPC 2023 初赛] 欺诈游戏
【题意】
求两方的均衡策略。
\(n \le 4 \times 10^5\)。
【分析】
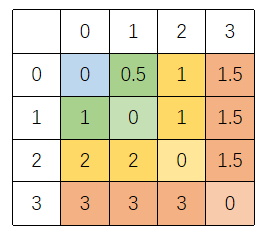
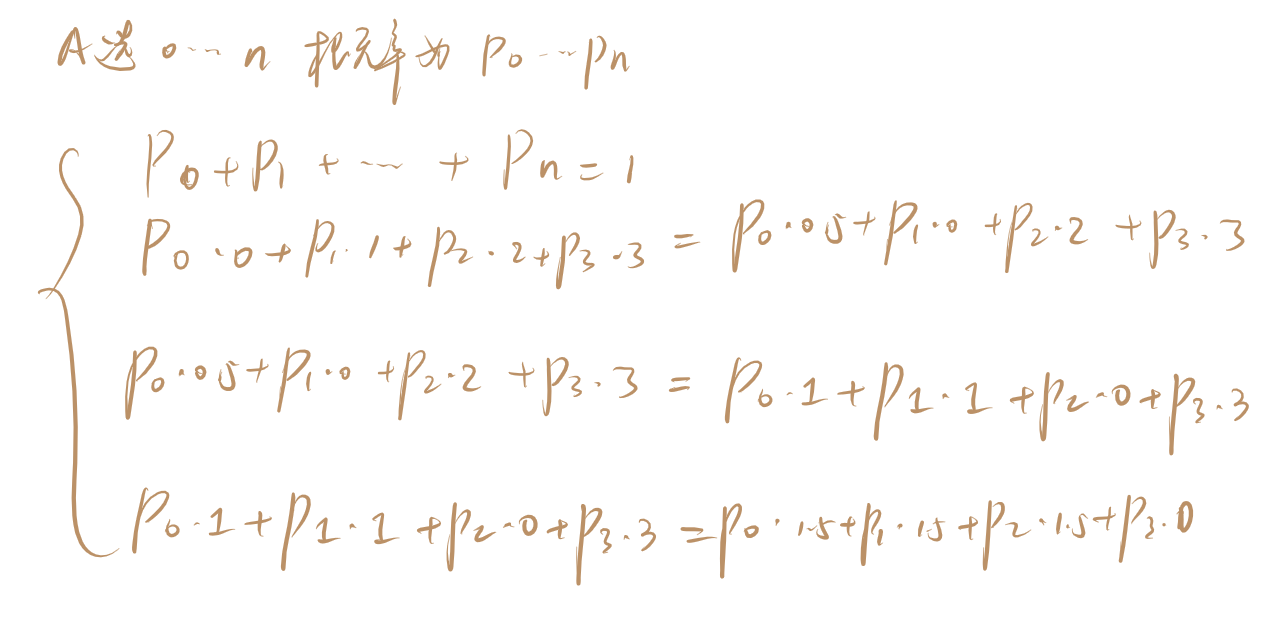
列出行列式:
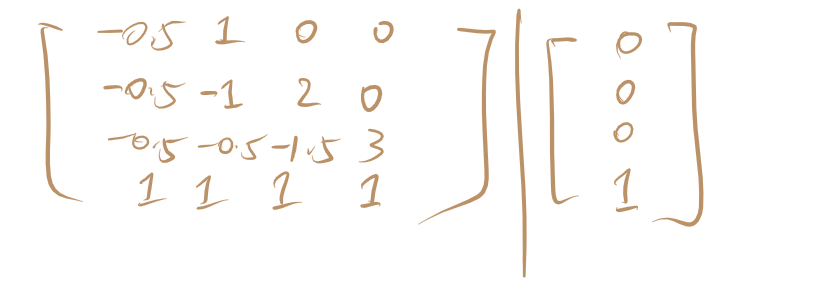
它是一个 \(d = 2\) 的类带状矩阵,可以 \(O(n^2 d)\) 的时间求出。
可能可以优化,但是我不会。而且这样太繁了。
它确实解出来是唯一解,那么就是纳什均衡点。
但是有一个比较好的解:注意到矩阵的右边和下面分数都是相同的,你可以直接认为是 \(n\) 层 \(2 \times 2\) 零和博弈,每层的两个决策是:选不选 \(i\)。
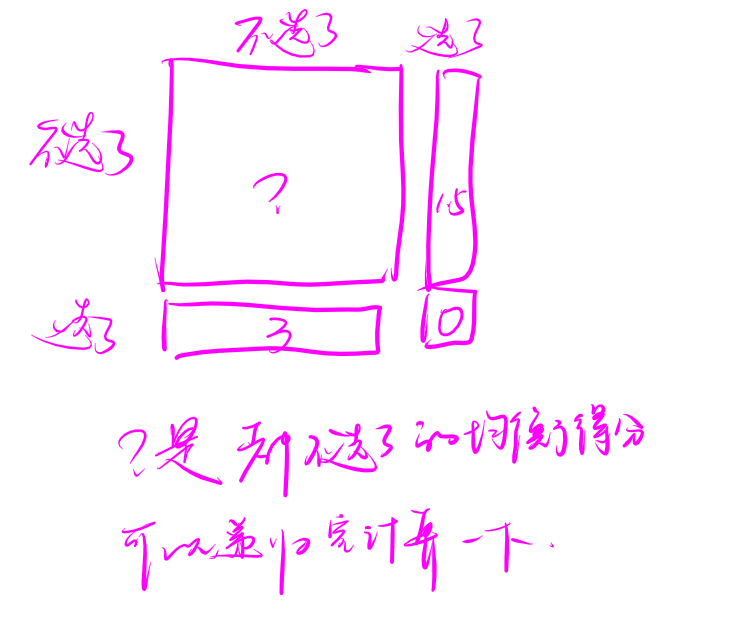
对于二维的情况,
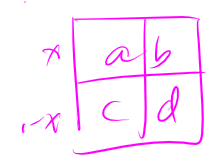
不难得到 \(x = \cfrac{c-d}{-a+b+c-d}\)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
//use ll instead of int.
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍!
//use std::array.
const int mod = 998244353;
int qpow(int x, int k) {
int res=1;
while(k) {
if(k&1)res=res*x%mod;
x=x*x%mod;
k>>=1;
}
return res;
}
int x[500050], y[500050];int p[500050],q[500050];
void qjc(int l, int r, int* a, int t) {
a[l] *= t; a[l] %= mod;
a[r+1] *= qpow(t,mod-2); a[r+1] %= mod;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n; cin >> n;
int a=0;
int inv2=qpow(2,mod-2);
// cerr <<"3/8="<<3*qpow(8,mod-2)%mod<<endl;
f(i,1,n){
// cerr << a << endl;
int b=i*inv2%mod,c=i,d=0;
int ap=a,bp=c,cp=b,dp=0;
// cerr << (c-d+mod) << " " << qpow(-a+b+c-d+mod+mod,mod-2) << endl;
x[i]=(c-d+mod)*qpow(-a+b+c-d+mod+mod,mod-2)%mod;
y[i]=(cp-dp+mod)*qpow(-ap+bp+cp-dp+mod+mod,mod-2)%mod;
a=x[i]*y[i]%mod*a%mod+x[i]*(1-y[i]+mod)%mod*b%mod+(1-x[i]+mod)*y[i]%mod*c%mod+(1-x[i]+mod)*(1-y[i]+mod)%mod*d%mod;
a %= mod;
}
// f(i,1,n)cout<<x[i]<<" "<<y[i]<<endl;
f(i,0,n+1)p[i]=q[i]=1;
qjc(0,0,p,x[1]);qjc(0,0,q,y[1]);
qjc(1,1,p,1-x[1]+mod);qjc(1,1,q,1-y[1]+mod);
f(i,2,n){
qjc(0,i-1,p,x[i]+mod);qjc(0,i-1,q,y[i]+mod);
qjc(i,i,p,1-x[i]+mod);qjc(i,i,q,1-y[i]+mod);
}
// f(i,0,n)cout<<p[i]<<" ";
// cout<<endl;
// f(i,0,n)cout<<q[i]<<" ";
// cout<<endl;
f(i,0,n) {
if(i==0);
else p[i]=p[i-1]*p[i]%mod,q[i]=q[i-1]*q[i]%mod;
}
f(i,0,n)cout<<p[i]<<" ";
cout<<endl;
f(i,0,n)cout<<q[i]<<" ";
cout<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/4/5
start thinking at 16:16
start coding at 22:11
finish debugging at 22:35
*/


