虚树
第一种定义方式
对于一棵树和若干个给定的点集,如果点集大小之和固定,这个点集的虚树是保留了点集信息的,并且点数和点集大小相关,如下图:
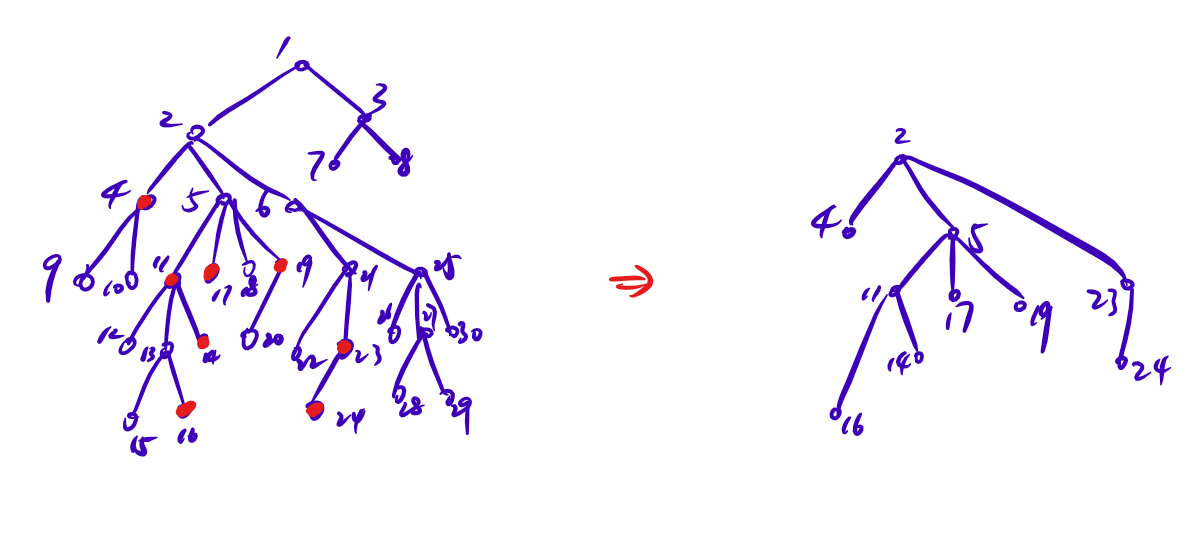
注意这里的虚树不包含点 \(11\) 和 \(16\) 中间的 \(13\),因为它并没有起到分叉的作用,如果加上这类点那么点数规模是不对的。
建立虚树
首先取出点集 \(S\),按照 dfn 排序,然后对点集加入每两个数之间的 lca,再按照 dfn 排序(先去重),然后对每两个相邻的点,取其 lca 并连接其与后一个点,如下图:
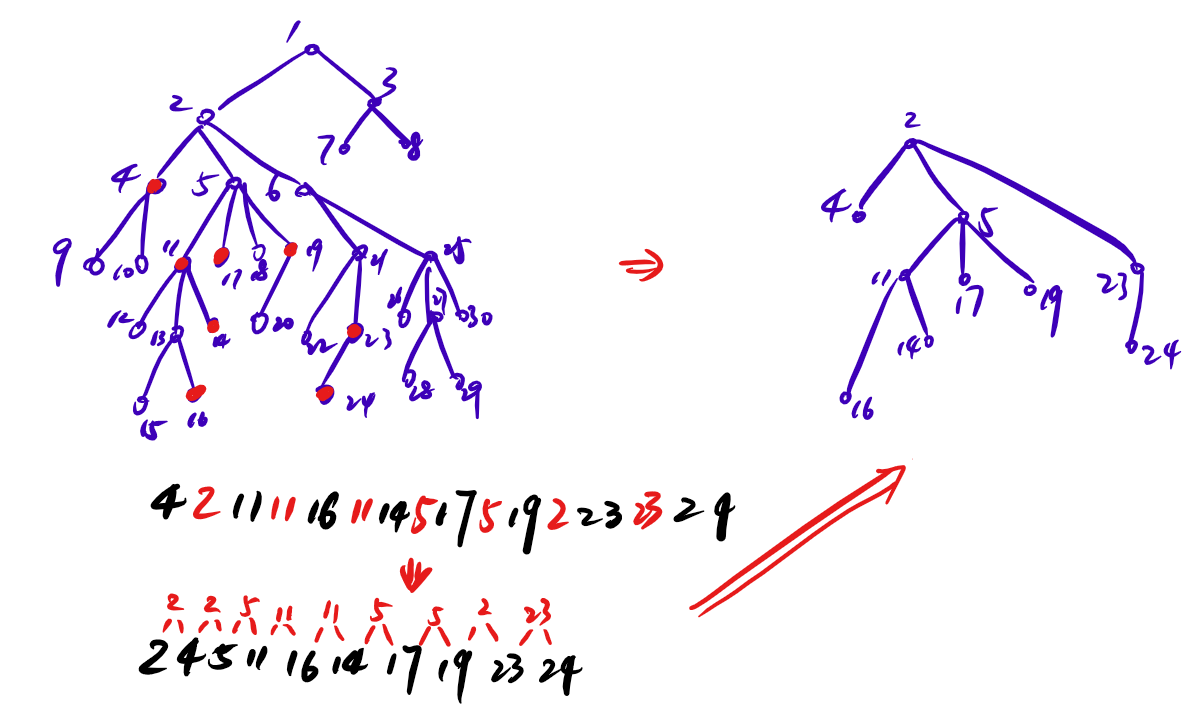
考虑证明:
首先,选出的点集就是最后虚树上的点集。
如果最后一步(取 lca)生成了某一个点:
- 如果是原树上两个点的 lca,那么显然在上一步被生成。
- 如果是上一步生成的 lca 和另一个点组成,那么这两棵子树上都有点,于是一定会生成该 lca。(区间内每一对相邻点的 lca 等于区间点 lca 等于区间两端点的 lca)
然后考虑选出的点集是否正确。
充分性:
对于虚树上的某一个点,要么其 \(\ge 1\) 个子树上有原点集点,要么其自己是原点集点。对于第一种情况,显然会被两个 dfn 相邻的点生成,对于第二种情况,显然已经选出。
必要性:
选出的点一定都是虚树上的点,显然。
最后考虑加边的正确性:
考虑某点的父亲。其一定是虚树点集内最近的一个祖先。它存在的话,要不自己存在,要不两个子树内都有点。显然这么做就是对的。
第二种定义方式
和第一种不同之处在于加入了点到其在第一种虚树祖先路径上所有的节点,如下所示:
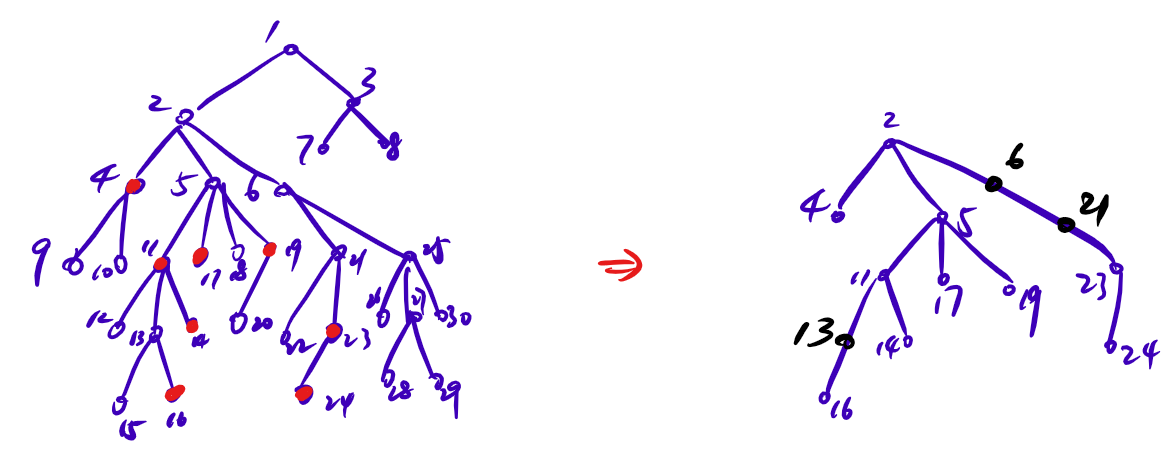
它没有点数性质,所以不是拿来维护,可能更普遍的方式是拿来考它的性质之类的。
性质
考虑对原点集 dfn 排序之后为 \(s\),假设原点集有 \(n\) 个点,那么其点数等于 \(\cfrac{\sum \limits_{i = 1} ^ n dis_{s_i, s_{i + 1}}}{2} + 1\),其中 \(i + 1\) 定义为循环加法,也即 \(i= n\) 的时候是 \(1\),其他时候是正常的 \(i+1\)。这是因为:我们考虑走一遍 \(4 \rightarrow 11 \rightarrow ... \rightarrow 4\) 的路,每条边正好走了一次,然后加上 \(1\) 就是点数。
考虑某一个点集的虚树大小的时候只需要按照 dfn 排序之后两两计算即可。不需要维护虚树。
另一种形式
考虑每一个节点到 \(root\) 的路径并,它就是虚树加上虚树的根到 \(root\) 那一段路。而那一段路也很好求,虚树的根就是所有原点的 lca,这个区间 lca 是好求的。
joisc 2023 Day 3 C
【题意】
给定一个 \(n\) 个点的树,有一个 \(m\) 个数的序列 \(a\),\(q\) 次询问,每次求从任意一个点开始走一条树上路径经过 \(a_l \sim a_r\) 中所有点的话,路径上经过至少一次的点数最少是多少。
【分析】
容易发现这题是求区间上点的虚树大小。
方法 1:
考虑莫队。
考虑加入某一个数。
如果直接加入并维护虚树,需要找到虚树上其最近祖先,二分线段树可以做到 \(\log^2\),但是显然过不去。
考虑虚树性质,可以 dfn 排序然后计算相邻两两距离之和。
如果使用不删除莫队,加入 \(\log\),用 set 维护,但是注意到这个题只需要查询 kth 的 rank,可以使用权值树状数组代替 set,具体这么做:
- 查询 rank:直接查询前缀和即可。
- 查询 kth:考虑树状数组上二分。
树状数组一种二分方式是直接模拟线段树二分(不同之处在于一个能求区间 kth,一个能求全局 kth)
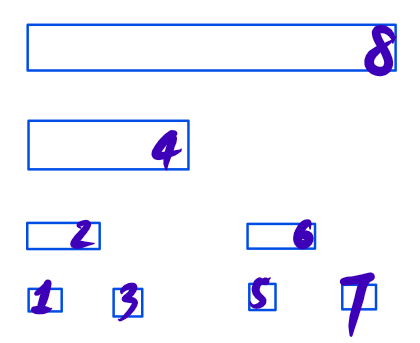
树状数组(记为 \(a\))长这样,我们考虑初始令 \(now = n, digit = \log_2 n - 1, k = k\)。这个 \(digit\) 的意思就是在哪一位。比如 \(digit = 2\) 就是在第三层(\(4\) 那一层)
如果 \(a_{now - 2^{digit}} \ge k\) 那么向左边走(\(now -= 2^{digit}\));否则向右边走(\(k -= a_{now - 2^{digit}}\))。不管往哪边走,\(digit--\)。
注意 \(n\) 要补到 \(2^n\),这个空间上要注意一下,但是由于后面的都是 \(0\),是不需要做其他事情的。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍!
//use std::array.
int n;
struct szsz {
int a[100010];
int lowbit(int x) {return x & -x;}
void add(int x, int k) {
while(x <= n) {
a[x] += k;
x += lowbit(x);
}
}
int rnk(int x) {
int res = 0;
while(x > 0) {
res += a[x];
x -= lowbit(x);
}
return res;
}
int kth(int k) {
int newn = 1 << ((int)log2(n - 1) + 1);
int now = newn, dig = log2(newn) - 1;
while(dig >= 0) {
if(a[now - (1 << dig)] >= k) {
now -= (1 << dig);
}
else {
k -= a[now - (1 << dig)];
}
dig--;
}
return now;
}
}tr;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> n; int q; cin >> q;
f(i, 1, q) {
int op; cin >> op;
if(op == 1){int x, k; cin >> x >> k; tr.add(x, k);}
else if(op == 2) {int x; cin >> x; cout << tr.rnk(x) << endl;}
else {int x; cin >> x; cout << tr.kth(x) << endl;}
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at h:mm
finish debugging at h:mm
*/
上面的这份代码,在点有权值的情况下,rnk 出来的是最大 rnk,kth 就是 kth。
于是我们成功把 set 改成了常数十分小的权值树状数组。这样 \(O(n \sqrt n \log n)\) 就可以在 4s 内卡过啦!(确信)
方法 2:
我们考虑把不删除改成不加入。(回滚莫队不仅能做不删除,也可以做不加入,具体方法就考虑某一块先计算 \(head \sim n\) 的答案,然后移动两边的指针)
这样做有什么好处呢?我们删除的时候直接用链表删除即可。(之前小瞧了这个数据结构,但是确实很有用)这样不用维护一棵平衡树,是 \(O(1)\) 的。考虑每一块插入过程。可以对 \(O(n)\) 长度的数组直接排序。暴力插入还是带一个 \(\log\),但是我们可以从右往左进行。这样做,这部分复杂度直接变成 \(O(n \log n)\),那么整体复杂度就是纯根号的。
方法 3:
考虑虚树的另一种形式:虚树根到原树根的一条链加上原树根到点集中所有点的并。
首先链是好求的,就一个区间 lca,这里不说了。重点是并怎么算。注意到这里就转化为了到根的链上问题了。如果不知道接下来干什么,接着想。
考虑扫描线的第二种形式,扫 \(r\),维护所有 \(l\) 的答案。考虑二维数点那个做法,维护最后一次出现位置。可以启发到这题上。注意到一个 \(r\) 是给 \(r\) 到 \(1\) 的链上这些点全部加入一次虚树,那么我们考虑维护时间戳,也就是每一个点是什么时候加入的虚树。
发现这个全部加入类似颜色段均摊处理的东西,考虑树剖之后是 \(\log\) 段连续段,这意味着每次扫描线右端点动了的时候只会插入 \(\log\) 段区间,所以这部分的时间复杂度是 \(O(\log^2 )\) 的。
考虑查询怎么做。额外维护一个权值树状数组拿来查询 rank。只需要实时维护颜色为某一个数的区间总大小即可。查询部分的时间复杂度是 \(O(\log)\) 的。
分几步:
- 树剖预处理。
- 扫描线,预先把所有区间打到 \(r\) 上。每次 \(r\) 动的时候,沿着 \(1 \sim c_r\) 的链走,更新颜色段,并在树状数组里更新。
- 处理查询,在树状数组里查询即可。树状数组支持 rank。
总时间复杂度 \(O(n + n \log^2 n + q \log n)\)。


