扫描线
1 扫描线
1.1 研究对象
在一个B维直角坐标系下,第i维坐标在一个整数范围[li,ri]间,内部的点集称为一个B维正交范围。
一般1维正交范围简称区间,2维正交范围简称矩形,3维正交范围简称立方体
对于B维正交范围,每一维都有两个限制,即有两条边(side),这样是一个2B-side的B维正交范围
如果部分维只有一个限制,则是一个A-side的B维正交范围
如果有一维没有限制,则这一维是平凡的,没有任何意义,可以简化到一个(B-1)维的问题
A-side的B维正交范围不能确定出是哪些维,如果维不对称的话需要特殊说明
1.2 模型
扫描线有两种模型:
- 对于一个静态的二维问题,我们可以使用扫描线扫一维,数据结构维护另一维
在扫描线从左到右扫的过程中,会在数据结构维护的那一维上产生一些修改与查询
如果查询的信息可差分的话直接使用差分,否则需要使用分治 - 另一种看待问题的角度是站在序列角度,而不站在二维平面角度
如果我们这样看待问题,则扫描线实际上是枚举了右端点r=1…n,维护一个数据结构,支持查询对于当前的r,给定一个值l,l到r的答案是什么
即扫描线扫询问右端点,数据结构维护所有左端点的答案
Notice:
其实看到任何范围修改查询问题,如果能差分的话,想都不想就差分是不会有问题的,我推荐直接这样做
典型的差分方法:
序列区间[l,r]差分为[1,r]-[1,l-1]的前缀
树上差分
二维前缀和的差分
1.3 处理二维正交范围的扫描线
问题可差分的时候,我们通过差分可以将一个4-side矩形查询问题变为两个3-side矩形查询问题的差
将第一维的1-side的区间(即前缀)扫描线扫掉,数据结构维护2-side的区间查询(这里两条边是相对的而不是相邻的),支持:
1.单点修改,区间查询
2.区间修改,单点查询
3.区间修改,区间查询
中的一种
(不要忘记了差分)
两大基础问题:
问题 1. 给一个长为n的序列,有m次查询,每次查区间[l,r]中值在[x,y]内的元素个数
我们考虑 轴表示序列, 轴表示权值。
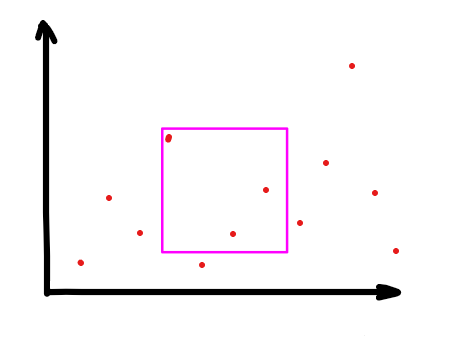
先差分,去掉序列维度的左端,然后对序列维度扫描线,维护竖着的数据结构,支持单点加点和区间查询和。
能使用树状数组尽量使用树状数组,这里可以差分(加法有逆)所以可以使用树状数组维护。
问题 2. 给一个二维平面,上面有n个矩形,每个矩形坐标[1,n]
有m次查询,每次查询一个二维平面上的点被多少矩形包含
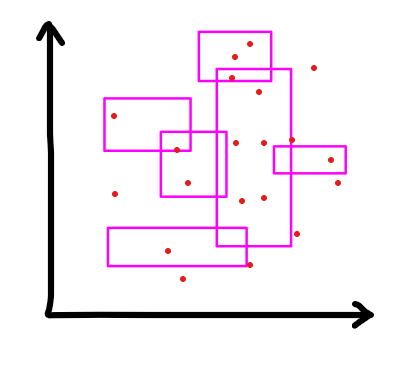
对某一维从左到右扫描线并且维护每个点被多少个矩形包含。有区间修改,单点查询,把区间修改差分掉变两个前缀修改,单点查询差分掉变两个前缀查询,可以用树状数组维护。
1.4 几个例子
一维数颜色
【题意】
给定长度为 的序列, 次查询区间中不同的数个数。
【分析】
思路 1:
我只想计算第一次在区间内出现的数的个数。考虑记 表示上一个和自己相同的数的位置,那么只统计 的 个数。两个维度分别是 ,是二维数点问题。可以扫描线树状数组。(直接用二维前缀和处理是 的,不适合本题,适合稠密的矩形)。
思路 2:
考虑扫描线扫右端点,维护所有左端点的答案。我们只对区间内第一次出现的数统计答案。也就是对 的位置的答案加上 。(也有些像 dp 数组一起进行递推,然后用数据结构维护)
思路 3:
扫描线的时候同时维护一个数组表示每个颜色最后一次出现的位置。然后修改是单点赋值为 ,查询是询问数组里面比 大的数有多少个。可以用 set 啥的做。而且插入都是从末尾插入。
思路 4:
分块,考虑每一块维护一个 bitset,线段树维护。
单次询问时间 。这个不需要打乱询问次序。
思路 5:
莫队。
支持单点修改和区间查询颜色数
现在操作中存在单点修改。怎么做:
思路 1:
依然考虑 pre 数组。
考虑一次修改造成的变化。

有三个点的 发生了改变。
考虑查询是二维平面上的数点,这些改变可以拆成一个单点 和 ,会作为基本单位对后续的询问产生影响。
对于每一个修改-询问二元组,都有一个这样的影响。但修改是不能快速找到位置的,所以我们考虑先要化简时间维度。
考虑 CDQ 分治。如果我们能够在 的时间完成所有时间位于 之前的修改和之后的询问,那么就可以解决这个问题。
注意到,这时候之前的修改和之后的询问变成了静态的。我们可以先花费 时间扫一遍修改,把每一次修改具体修改了什么点确定了。然后考虑问题变成了:平面上有 个点,每个点权值为 或者 ,有若干个矩形,求每个矩形内权值和。
这显然还是二维数点问题。把 3-side 的矩形差分为两个 2-side 的矩形,然后扫描线扫 ,树状数组维护前缀和即可。
支持区间覆盖和区间查询颜色数
操作中出现了区间覆盖(P4690)。
思路 1:
我们考虑和单点修改版本差距是什么。是修改操作,也就是 的修改换了。
考虑颜色段均摊。删除颜色段个数是有保障的。那么我们可以方便地维护颜色段。最后可以方便地计算 pre。(如果在段内但不在段首,,否则找上个颜色)但是有这个还不够。只有这个性质的话,cdq 分治的正确性依然无法保障,因为不是和分治的段数相关而是和 相关了。
我们还需要一个关于 值改变个数的结论。
考虑颜色段替代的时候有什么影响:
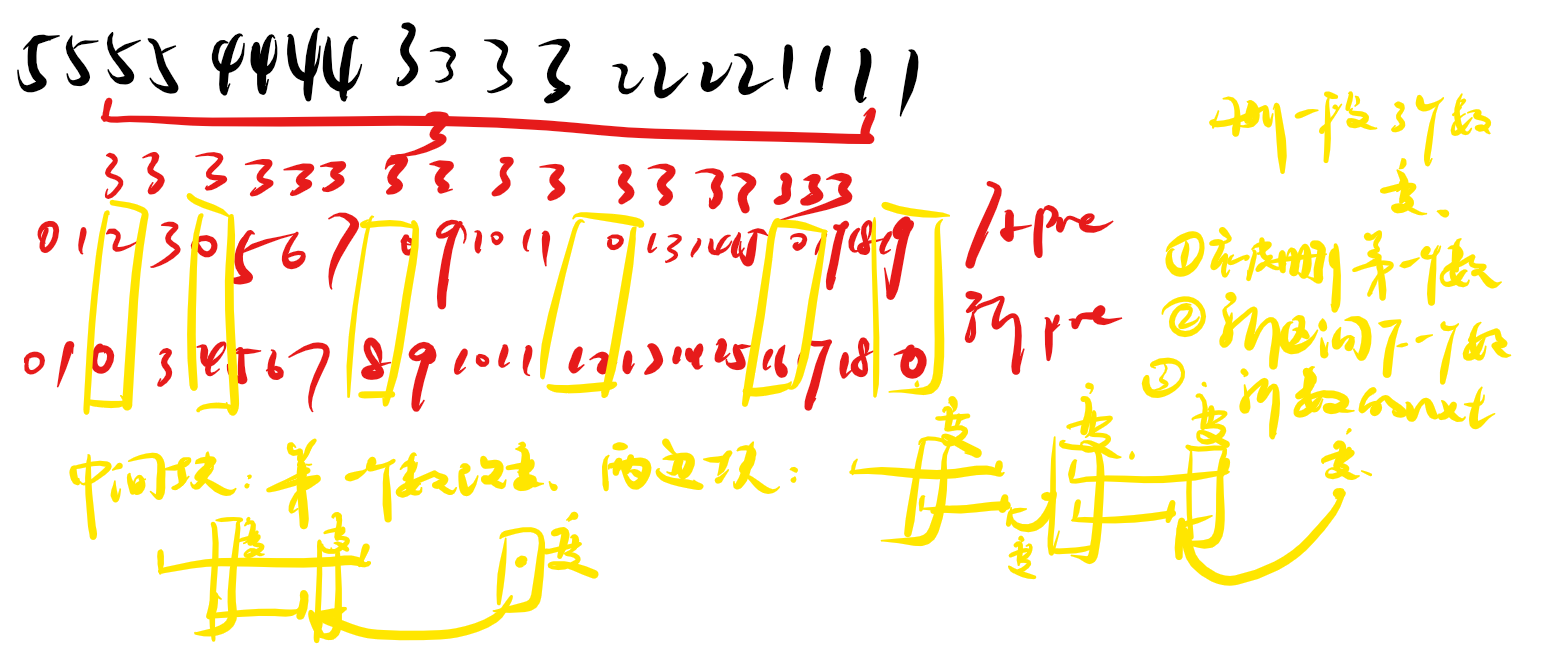
可以发现删除一个连续段最多对 产生 的影响。因此 次覆盖好像是 的?
确实是这样,但是你注意 CDQ 分治某一层的总共影响就是 的,所以我们只需要模拟 个影响。
于是时间复杂度 。
问题你怎么写 CDQ 分治,怎么维护 pre 的修改,怎么做到空间复杂度尽量好?
-
对于 pre 的修改,虽然我们删掉一次颜色之后可以得知哪些点改变了,但是这样写会有很多分讨,不好。正确的做法是,把所有可能改变的地方丢到 set 里面,把所有颜色段修改维护完,然后重新对 set 里面的点求 pre。
-
对于时间分治的 cdq 怎么写:考虑分三步走:
- 统计 内修改对 内查询的影响。并且撤销影响。
- 递归到 区间。
- 递归到 区间。
- 对 内所有修改造成实际影响。
这样,递归入某一个区间的时候, 内的修改都已经造成实际影响,而其他的没有造成影响。
一个修改最多被执行 次,是对的。
-
考虑维护什么。首先要维护颜色段,以及被修改的点的 set,然后要备份颜色段,没了。空间复杂度 。
二维数颜色
(待填坑)
一些转化
-
给定一棵 个节点的树,点和边都有编号。 次查询,每次给出 ,查询如果只保留树上点编号在 的点,边标号在 的边,有多少连通块,此时 和 连通等价于 并且 在树上简单路径中每个点和边编号都在 内。
转化:连通块个数转化为点数减边数,边 有用转化为 。转化为二维数点。 -
给定很多模式字符串,每次查询时给两个字符串s1,s2,问有多少模式字符串前缀是s1,后缀是s2
转化:字符串“前缀是 x” 转化成“是 trie 树某个节点的子树”,每个串挂在 trie 的某点上;后缀就对反串再建一个。变成子树交问题。转化成 dfn 上区间,二维数点。 -
给一个长为n的序列,m次查询:
如果将区间 [l,r] 中所有数都+1,那么整个序列有多少个不同的数?
询问间独立,也就是说每次查询后这个修改都会被撤销
转化:考虑 是两个维度。一般考虑利用不同值对答案贡献独立的性质,对每一个元素/值求贡献,然后用数据结构批处理。这题用出现的数算比较不好算,考虑算什么时候某个数不出现。
什么情况下全局没有x这个值呢?
所有原来为x的数都被加上了1;所有原来为x-1的数都没有被加上1。
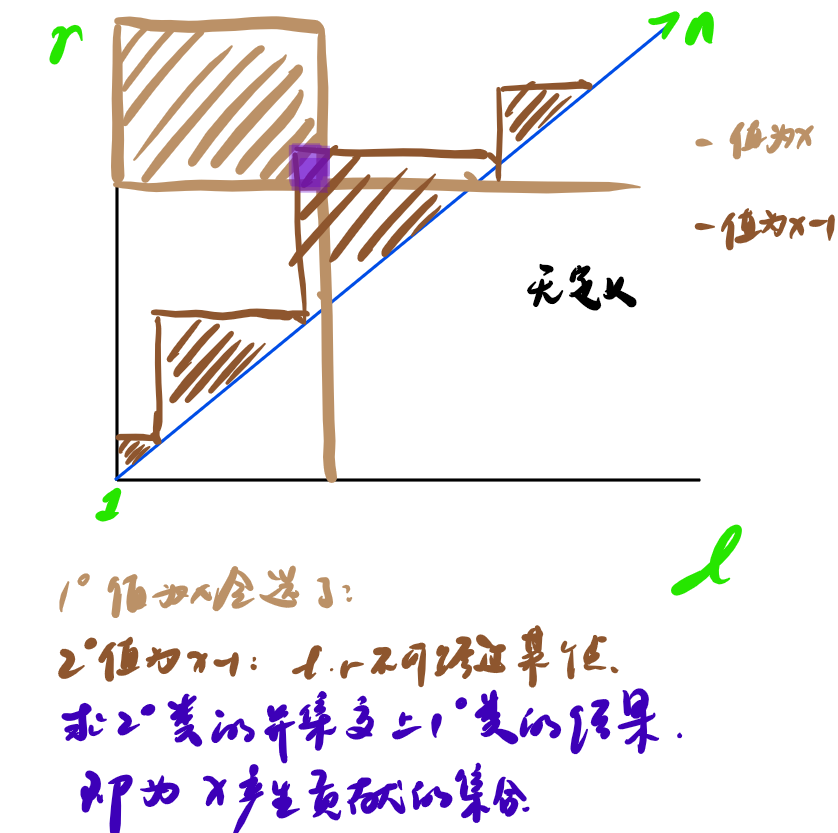
转化为了,有多少个矩形包含某个点。矩形个数就是 。 -
给定一个序列,每次查询区间中出现偶数次的数的异或和
转化:如果是奇数次,等价于区间异或和。偶数次怎么办?
可以转化为,区间所有出现过的颜色的异或和,异或上,奇数次颜色的异或和。
可以转化为区间数颜色,但是某个点带权值,是带权值二维数点问题。依然可以扫描线+树状数组解决,维护异或和即可。 -
矩形面积并
维护区间最小值和最小值出现次数,有区间覆盖。这个只能线段树维护,合并的时候,若二者min相等,则累计min出现次数,否则取一边的作为答案;如果出现次数是 ,那么 min 出现次数就是 出现次数;否则出现次数是 。
1.5 区间子区间/历史和问题
给一个序列,每次查询区间有多少子区间满足某个条件
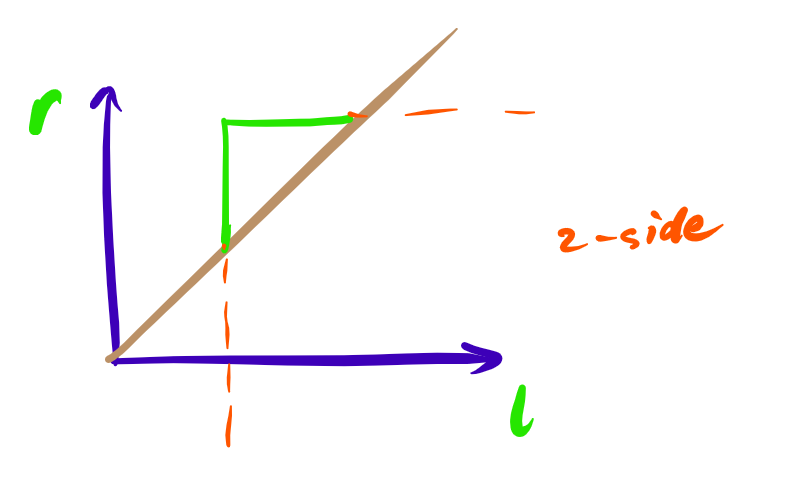
考虑区间看做二维平面上一个点,然后所有子区间转换为矩形内所有点。
由于区间 满足 ,所以实际上是一个三角部分,可以看做一个 2-side 矩形。
有的题询问所有区间的信息,这时候可能就需要条件反射想一下第二种扫描线,一般会比第一种扫描线更好做,第二种扫描线扫描了右端点提供了更多局部信息。
一些转化
- 有两个数列 , 次询问每次给定 ,求 的值。(NOIP2022 T4)
考虑最值分治,然后转化为一些矩形赋值 。不妨看成矩形乘法。然后询问是 2-side 的,所以不妨从右往左扫。
考虑可以把这个矩形乘法: 时刻内 乘以 。可以在扫描线上拆成: 时刻 乘以 , 时刻 除以 。
对于线段树部分:我们有两种标记,一种 ,一种 ( 分别是当前和和历史和)注意标记合并的时候是某个节点原本的标记先于父亲节点的标记。然后这两个标记都是可以下传的。这题标记比较少,如果多的话,可以看成矩阵乘法再去传。
注意到这个除法有点难搞。怎么办呢?有人说改成区间赋值,那样的话标记会更多。注意到答案范围 以下,一种方法是用 __float128 去做,这个相对精度是 的,最多不会 ,所以我们每个数 然后向 0 舍入即可。但是这样会非常的慢。第二种方法是三模合并,取三个质数做模数,求出答案之后 crt 合并。这种方法一定要确保取模没问题,以及 crt 合并的时候要先 mod ,否则会寄!
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
#define double __float128
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍!
//use std::array.
int ql[250010], qr[250010], qa[250010], qb[250010];
struct line{int l, r; int k;};
vector<line> li[250010]; //时间节点,从后往前做
//扫描线的时候
//在第一维是 x 的时候,第二维度 [l, r] 区间乘 k
struct rect{int l, r, x, y; int k;};
vector<rect> re;
struct query{int l, r, id;};
vector<query> qu[250010];
uint64_t ys[3][250010];
int mod;
//矩形乘 k
//41, 53, 89
int qpow(int x, int k) {
x %= mod;
int res = 1;
while(k) {
if(k & 1) res = res * x % mod;
x = x * x % mod;
k >>= 1;
}
return res;
}
struct sgt {
int sum[1000010], his[1000010], tag1[1000010], tag2[1000010];
//A, B, A*=tag1, B+=tag2A(B 先加,A 后加)
void circ1(int &a, int &b, int la, int lb, int ra, int rb) {a = la + ra; b = lb + rb; a %= mod; b %= mod;}
void circ2(int &a, int &b, int tg1, int tg2) {b += tg2 * a; a *= tg1; b %= mod; a %= mod;}
void circ3(int &t1, int &t2, int tg1, int tg2) {t2 += tg2 * t1; t1 *= tg1; t2 %= mod; t1 %= mod;}
void build(int now, int x, int y) {
//初始化为 1
if(x == y) {sum[now] = y - x + 1; his[now] = 0; tag1[now] = 1; tag2[now] = 0;return;}
int mid = (x + y) >> 1;
build(now * 2, x, mid); build(now * 2 + 1, mid + 1, y);
circ1(sum[now], his[now], sum[now * 2], his[now * 2], sum[now * 2 + 1], his[now * 2 + 1]);
tag1[now] = 1, tag2[now] = 0;
}
void pushdown(int now) {
if(tag1[now] != 1 || tag2[now] != 0) {
circ2(sum[now * 2], his[now * 2], tag1[now], tag2[now]);
circ2(sum[now * 2 + 1], his[now * 2 + 1], tag1[now], tag2[now]);
circ3(tag1[now * 2], tag2[now * 2], tag1[now], tag2[now]);
circ3(tag1[now * 2 + 1], tag2[now * 2 + 1], tag1[now], tag2[now]);
tag1[now] = 1; tag2[now] = 0;
return;
}
}
void mul(int now, int l, int r, int x, int y, int k) {
//区间 [l, r] *= k
if(l >= x && r <= y) {
// cerr << "before " << now << " " <<l << " " << r << " " <<x<<" "<<y<<" "<<k<<", sum, tag1 = " << sum[now] << ' ' << tag1[now] << endl;
sum[now] *= k; sum[now] %= mod;
tag1[now] *= k; tag1[now] %= mod;
// cerr << "fix " << now << " " <<l << " " << r << " " <<x<<" "<<y<<" "<<k<<", sum, tag1 = " << sum[now] << ' ' << tag1[now] << endl;
return;
}
if(l > y || r < x) return;
int mid = (l + r) >> 1;
pushdown(now);
mul(now * 2, l, mid, x, y, k);
mul(now * 2 + 1, mid + 1, r, x, y, k);
circ1(sum[now], his[now], sum[now * 2], his[now * 2], sum[now * 2 + 1], his[now * 2 + 1]);
}
void add(int now, int l, int r, int x, int y) {
//B += A, (x, y) always be (1, n).
if(l >= x && r <= y) {
his[now] += sum[now]; if(his[now] >= mod) his[now] -= mod;
tag2[now] += tag1[now]; if(tag2[now] >= mod) his[now] -= mod;
return;
}
return;
}
int query(int now, int l, int r, int x, int y) {
//不存在的部分都是 1, 需要减掉。
//减掉多少:(n-l+1)*r - (r-l+2)*(r-l+1)/2
if(l >= x && r <= y) {
return his[now];
}
if(l > y || r < x) return 0;
int mid = (l + r) >> 1;
pushdown(now);
return (query(now * 2, l, mid, x, y) + query(now * 2 + 1, mid + 1, r, x, y)) % mod;
}
void dfs(int now, int l, int r) {
// cerr << "node number #" << now<<", (l, r) = " << l << " " << r << endl;
// cerr << "sum, his: " << sum[now] << " " << his[now] << endl;
// cerr << "tag1, tag2: " << tag1[now] << " " << tag2[now] << endl;
if(l == r) return;
pushdown(now);
int mid = (l + r) >> 1;
dfs(now * 2, l, mid); dfs(now * 2 + 1, mid + 1, r);
}
}t;
int T, n; int q;
int rnk[250010];
void zzfz(int* x) {
set<pii> s; s.insert({n, 1}); f(i, 1, n) rnk[x[i]] = i;
for(int i = n; i >= 1; i--) {
int pos = rnk[i];
auto it = s.lower_bound({pos, 0});
int l = (*it).second, r = (*it).first;
//[l, pos], [pos, r] *= i
re.push_back({l, pos, pos, r, i});
s.erase(it);
if(pos - 1 >= l) s.insert({pos - 1, l});
if(r >= pos + 1) s.insert({r, pos + 1});
}
}
void unpack() {
for(rect i : re) {
li[i.r].push_back({i.x, i.y, i.k});
li[i.l - 1].push_back({i.x, i.y, qpow(i.k, mod - 2)});
}
}
void dealq() {
f(i, 1, q) {qu[ql[i]].push_back({1, qr[i], i});}
}
void doit(uint64_t* ans) {
re.clear(); f(i, 1, n) li[i].clear(), qu[i].clear();
zzfz(qa); zzfz(qb); unpack(); dealq();
t.build(1, 1, n);//t.dfs(1, 1, n);
for(int i = n; i >= 1; i--) {
// cerr << "lines of " << i << endl;
// for(line it : li[i]) cerr << it.l <<" " << it.r << " " << it.k << endl;
for(line it : li[i]) {
t.mul(1, 1, n, it.l, it.r, it.k); //t.dfs(1, 1, n);
}
t.add(1, 1, n, 1, n);
// t.dfs(1, 1, n);
for(query it : qu[i]) {
__int128_t res = t.query(1, 1, n, it.l, it.r);
// cerr << i << " " << res << endl;
res -= (n - i + 1) * it.r - (it.r - i + 2) * (it.r - i + 1) / 2;
res = (res % mod) + mod; if(res >= mod) res -= mod;
// cerr << "minus: " <<(n - i + 1) * it.r <<" "<< (it.r - i + 2) * (it.r - i + 1) / 2 << endl;
ans[it.id] = (uint64_t)res;
}
}
}
const __int128_t mt = ((__int128_t)~0ull + 1);
uint64_t crt(int id) {
// cerr << qpow(1000, mod - 2)
__int128_t res = 0;
__int128_t md[3] = {998244341, 998244353, 998244389};
// cout << ys[0][id] << " " << ys[1][id] << " " << ys[2][id] << endl;
__int128_t bm = md[0] * md[1] * md[2];
// cout << (uint64_t)(bm*2) << endl;
// cerr << (ll)(bm / md[0]) << endl;
// res += (__int128_t)ys[0][id] * md[1] * md[2] % mt * qpow(md[1] * md[2], md[0] - 2) % mt;
// res += (__int128_t)ys[1][id] * md[0] * md[1] % mt * qpow(md[0] * md[2], md[1] - 2) % mt;
// res += (__int128_t)ys[2][id] * md[0] * md[2] % mt * qpow(md[0] * md[1], md[2] - 2) % mt;
f(i, 0, 2) {
mod = md[i];
// cout << (ll)((bm / md[i]) * qpow(bm / md[i], md[i] - 2) % (md[i] )) << endl;
res += (__int128_t) ys[i][id] * (bm / md[i]) % bm * qpow(bm / md[i], md[i] - 2) % bm;
}
res %= bm;
res %= mt;
return res;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
freopen("match.in", "r", stdin);
freopen("match.out", "w", stdout);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> T >> n;
f(i, 1, n) cin >> qa[i];
f(i, 1, n) cin >> qb[i];
cin >> q;
f(i, 1, q) cin >> ql[i] >> qr[i];
// cerr << "rectangles: " << endl;
// for(rect i : re) cerr << i.l << " " << i.r << " " << i.x << " " << i.y << " " << i.k << endl;
mod = 998244341; doit(ys[0]);
mod = 998244353; doit(ys[1]);
mod = 998244389; doit(ys[2]);
// return 0;
f(i, 1, q) cout << crt(i) << endl;
// t.build(1, 1, n);t.dfs(1, 1, n);
// for(int i = n; i >= 1; i--) {
// cerr << "lines of " << i << endl;
// for(line it : li[i]) cerr << it.l <<" " << it.r << " " << it.k << endl;
// for(line it : li[i]) {
// t.mul(1, 1, n, it.l, it.r, it.k); //t.dfs(1, 1, n);
// }
// t.add(1, 1, n, 1, n);
// t.dfs(1, 1, n);
// for(query it : qu[i]) {
// __int128_t res = t.query(1, 1, n, it.l, it.r);
// cerr << i << " " << res << endl;
// res -= (n - i + 1) * it.r - (it.r - i + 2) * (it.r - i + 1) / 2 ;
// cerr << "minus: " <<(n - i + 1) * it.r <<" "<< (it.r - i + 2) * (it.r - i + 1) / 2 << endl;
// ans[it.id] = (uint64_t)res;
// }
// }
// cerr << "alive\n";
// f(i, 1, q) cout << ans[i] << endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
值域是 n
对区间进行最值分治,分治出来一堆矩形,拆成一些线,右边 *x, 左边 /x,放到 vector 里
从右到左去对 vector 里面的线进行操作,也就是线段树的区间 *x
线段树维护 区间和,tag(乘以多少),初始所有信息都是 1
标记:乘以多少,信息和标记:乘法,信息和信息:加法
区间内所有数乘以 k,区间和乘以 k
否则可以从下面到上面 pushup
除法直接当做 double 就好了,实际上乘完是 int,最后 +0.5,转为 int 即可。
(这就是四舍五入)
start coding at h:mm
finish debugging at h:mm
*/
CF1824D LuoTianyi and the Function
【题意】
给定序列 ,定义 为:
- 如果 , 定义为最大的 使得 。
- 否则,。
给定 ,求 。
【分析】
这个问题一看是区间子区间问题,想到在二维平面上做:对于某一个数字 ,如果其出现位置有 ,那么对于 , 这个矩形内取 。
问题转化为区间取 ,查询历史和。这个问题可以用吉老师线段树解决,但是要维护的信息一看就多(而且会被凉心出题人卡)
其实这样做是繁了。正解是不需要这个的。
正解是第二种扫描线,扫描线扫右端点,维护所有左端点的答案,然后有一些历史和。
首先观察左端点的答案长什么样。
即,每一个数的最后一次出现位置集合为 的话, 的取值为 之后第一个 中元素。
往右边移动 的时候,可能有一个数会被覆盖。有两段 会改变,可以认为是区间加历史最值线段树:
从原题到“有一些区间加,查询历史最值”的转化,用一个 set 维护即可。
下面考虑区间加历史最值线段树的实现细节,由于若干次写的时候都犯了一些错,有必要讲细一些。
首先,我们线段树的每一个节点上有信息和标记两个部分。某一个节点的信息,等于其节点本身信息 上祖先所有节点标记;祖先标记反映了对整个区间已经做过的,但是还没有在下面体现的所有操作之和。
其次,考虑一个“修改”操作。可以认为对包含的区间做了一个 (区间信息乘标记,区间标记乘标记),对象是“修改”操作代表的标记。对不是包含的区间,是在下面做完修改 pushup 的。所以 pushup 环节在修改里是很重要的不要漏掉。
考虑“pushdown”操作。可以认为是对 和 分别 上 。因此这一部分和修改操作的“包含”部分完全一致,有高度的模板性。甚至是对于比较“另类”的 (例如吉老师线段树的如果 那么直接往下递归)也是一致的,在 pushdown 函数里面长得一模一样。(“修改”向下递归到的是“修改”函数,“”向下地递归到的是“”函数,但是两者是统一的,因为一旦包含,往下在修改函数里也只是一直进入包含部分罢了。)
搞清楚这俩是同一个东西之后,我们需要实现: 个 ,以及其他细枝末节的东西(调用这三个 的接口和 pushdown)。主要错误都出现在 个 上。
现在考虑对于区间加历史和线段树,需要打什么标记?需要有什么标记不是人为规定出来的,而是我们看看若干个“修改”叠加会发生什么。
我们有这两种“修改”:。我习惯令标记含义是先 再 ,所以考虑:
所以我们规定标记由三元组 构成。但是这里注意了:对于“加法”,我们只能考虑给区间内每个 都加上一个常数,也就是 的含义其实是“区间内每个单独的位置的 加上 ”。而 的含义可以是每一个位置的 都加上该位置的 ,也可以是整个 加上整个 ,都一样(其实第一种理解方式应当是正统)。 的定义不是关键,重点是 的定义需要很注意,对信息和标记的询问很有帮助(不注意这些看似简单的细节,就是会写错掉,所以要认真思考每一个标记的含义)
以上面的理论为依据可以写出一棵这样的线段树:
struct SGT{
int A[4000200], B[4000200], k[4000200], X[4000200], b[4000200]; //B += kA + b, A += x
void circ1(int now, int lc, int rc) {
A[now] = A[lc] + A[rc]; B[now] = B[lc] + B[rc]; return;
}
void circ2(int now, int l, int r, int k0, int x0, int b0){
B[now] += k0 * A[now] + b0 * (r - l + 1); A[now] += (r - l + 1) * x0;
}
void circ3(int now, int l __attribute__((unused)), int r __attribute__((unused)), int k0, int x0, int b0){
k[now] += k0; b[now] += k0 * X[now] + b0; X[now] += x0;
}
void build(int now, int l, int r) {
if(l == r) {A[now] = 0; B[now] = 0; k[now] = X[now] = b[now] = 0; return; }
int mid = (l + r) >> 1; build(now * 2, l, mid); build(now * 2 + 1, mid + 1, r);
circ1(now, now * 2, now * 2 + 1);
}
void pushdown(int now, int l, int r) {
if(k[now]!=0 || X[now]!=0 || b[now]!=0) {
int mid=(l+r)>>1;
circ2(now*2,l,mid,k[now],X[now],b[now]);circ2(now*2+1,mid+1,r,k[now],X[now],b[now]);
circ3(now*2,l,mid,k[now],X[now],b[now]);circ3(now*2+1,mid+1,r,k[now],X[now],b[now]);
k[now]=X[now]=b[now]=0;
}
}
void add(int now, int l, int r, int x, int y, int t) {
if(l>=x&&r<=y) {
circ2(now, l, r, 0, t, 0); circ3(now, l, r, 0, t, 0); return;
}
if(l>y||r<x)return;
int mid=(l+r)>>1; pushdown(now,l,r); add(now*2, l, mid, x, y, t);add(now*2+1, mid+1, r, x, y, t);
circ1(now, now*2, now * 2 + 1);
}
void his() {
circ2(1, 1, n, 1, 0, 0); circ3(1, 1, n, 1, 0, 0); return;
}
int que(int now, int l, int r, int x, int y) {
if(l >= x && r <= y) return B[now];
if(l > y || r < x) return 0;
int mid = (l + r) >> 1; pushdown(now, l, r); circ1(now, now * 2, now * 2 + 1);
return que(now * 2, l, mid, x, y) + que(now * 2 + 1, mid + 1, r, x, y);
}
}sgt;
那么这题就结束了。但是我依然想要说一件事情:线段树写挂怎么调。首先结构上的问题是好查的,一般来说难查的是有关标记含义的问题。这时候可以先重新理一下,看看标记含义有没有错漏。然后下一步是对线段树进行 dfs。dfs 过程可以选择实时 pushdown(效果就像每次修改直接到叶子)也可以不 pushdown(这时候每一个位置的信息不一定是正确的,但是可以观察标记和信息的运作情况)。可以选择 这样的线段树来模拟,有助于快速发现错误。
1.6 分治
如果信息不支持差分为 3-side,那么我们需要分治。
考虑某一个询问矩形 ,将其在 轴上切开变成两个 3-side 矩形,转化为历史和询问。
考虑对时间轴建立分治结构 ,每一个分治结构是一个独立的部分,处理方式是从 往左扫,有一些区间修改,有一些区间查询历史信息。然后从 往右扫,一样。询问有 ,将这些信息合并到 的答案里面。
注意虽然是 往左右边扫,但是这个处理过程属于 这个区间,不要搞混了。
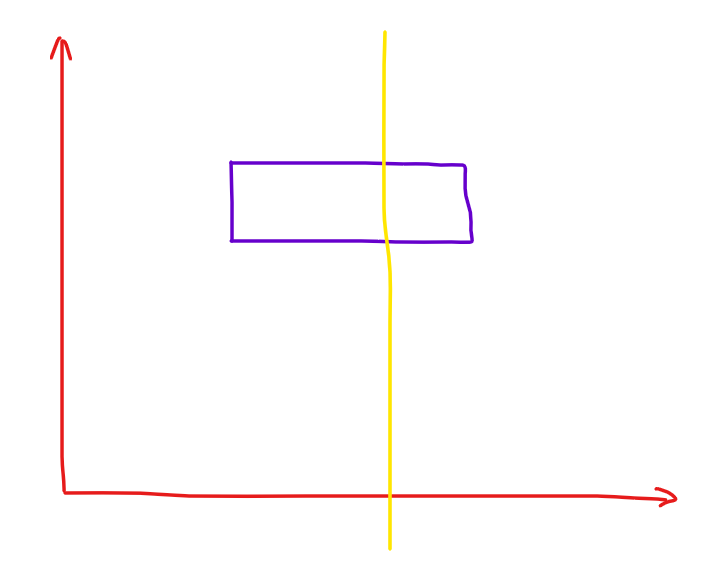
是区间查询的范围我们不关心, 这个区间在分治到 的时候处理当且仅当 跨过 并且在 内。
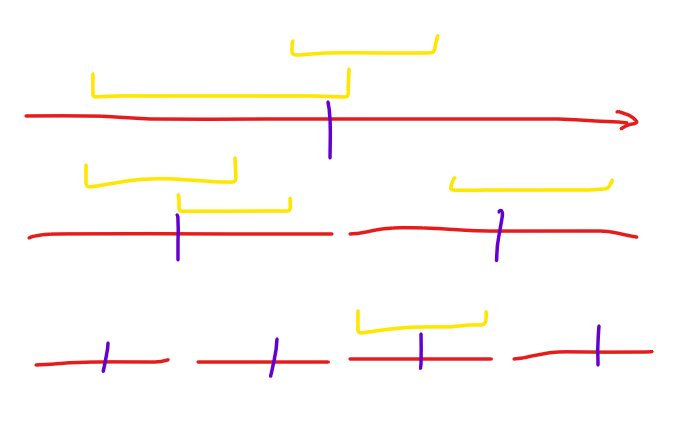
注意这个跨过的意义是可以认为没有其中一个边界,那么如果其右端点正好是 (认为两边是 )那么依然将其划分到这个位置。
注意当 轴范围 的时候不会走到 的区间,如果特判 的情况回溯会有 的常数。(注意一定要特判,不然 就寄了)
这样划分之后,每一个区间刚好被分到一次,其答案就是 两边两段历史和的信息合并。
考虑矩形修改,矩形询问。对于修改矩形,依然给它放在分治的区间上。
但是这个“放”的意义是对某一些区间上是一个区间修改。所以考虑其放的时间复杂度。对于完全被这个区间覆盖的区间,就直接打上标记,不需要处理了;对于部分覆盖的区间,需要处理。所以每一层每一个区间最多有 个要处理的位置,一个区间在整个分治结构上面会拆分为 个修改操作。
实现上,考虑下传的时候判断一下是否 ,如果是的话,就不下传到左儿子,而是放一个全局修改操作在左儿子。
但是全局修改操作是不好合并的(因为每一个修改操作其实是对 y 轴的 区间做一个修改操作)而且如果一个一个进行修改的话复杂度就不对了。所以我们考虑类似标记永久化的东西,就是走到某个点,把这个点上的全局修改做了,然后做自己的部分修改并且撤销(撤销的意思是对于一个区间修改拆成扫描线上两个单点修改,其加在一起效果对 这个量是 ),然后递归到儿子上,这时候儿子必然也需要这个全局修改,然后在线段树上只存在所有祖先的全局修改了,所以只需要对儿子这里第一次出现的区间修改做一遍,等所有儿子做完之后,递归回去的时候把所有全局修改撤销掉。
这样做就是普通的区间线段树操作,时间复杂度就是对的。
有修改也有询问的话,你可以事先把所有区间的 处理一下,然后挂上询问,挂上修改,“挂”的意思是从根递归下去找它应该在的位置。然后所有东西做完之后,再从根节点开始 dfs 这个分治结构,dfs 到一个点的时候从 向两边做扫描线,处理所有东西。
挂的时候,像正常扫描线一样把 挂在 的某一个“重新标号的时间”上,重新标号是这样的:
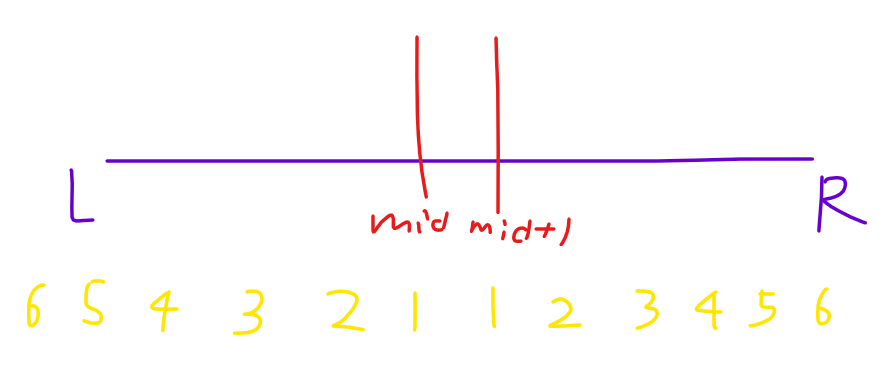
这样标号之后,只需要处理 的和 时间上的操作(注意线段树的 是 y 轴值域),之所以 左边还有一个点是为了差分之后的撤回操作,这个操作是必须要做的,否则传下去的线段树有问题。
对于 轴长度是 ,修改和询问个数分别是 的问题,时间复杂度:。
如果 同阶,可以利用多叉分治结构进行进一步平衡,但是我不会。
P6109 rprmq1
【题意】
矩形加,矩形查询最大值。
【分析】
分治的部分刚刚说过了,剩下线段树里面的东西。
考虑信息 ,标记 ,表示区间内 然后 。
三种合并很好推导,只要抓住先后顺序。
但是要注意的是,很容易出现 typo,你检查的时候一定要检查清楚。
随机数据很强,但是样例绝对很弱!
对拍显然是可以写的。
#include<bits/stdc++.h>
using namespace std;
#define int long long
//use ll instead of int.
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 1e16;
// #define cerr if(false)cerr
#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍!
//use std::array.
struct qj {int l, r; int x, y; int k; bool operator< (qj op) {return l < op.l;}}; // 原始区间
struct xw {int l, r, x, y; }; //原始询问
int n,m1,m2;
int ans[500040];
struct line {int l, r, k; }; //y 轴上 [l, r] 区间加 k
struct query {int l, r; int id;}; //询问 [l, r] 的历史和,然后 ans[id] 对这个历史和取 max
//x: [l, mid] / [mid + 1, r]
vector<line> li[50040];
vector<query> qu[50040];
struct SGT {
int A[200010], B[200010]; int k[200010], t[200200];
void build(int now,int l,int r) {
A[now]=B[now]=k[now]=0; t[now]=-inf;
if(l == r) return;
int mid=(l+r)>>1;
build(now*2,l,mid); build(now*2+1,mid+1,r);
}
void circ1(int &a, int &b, int al, int bl, int ar, int br) {a = max(al, ar); b = max(bl, br);}
void circ2(int &T, int &K, int t1, int k1, int t2, int k2) {T = max(t1, k1 + t2); K = k1 + k2;}
void circ3(int &a, int &b, int ap, int bp, int T, int K) {a = ap + K; b = max(bp, ap + T);}
void pushdown(int now) {
if(k[now]!=0 || t[now] != -inf) {
circ3(A[now*2], B[now*2], A[now*2], B[now*2], t[now], k[now]);
circ3(A[now*2+1], B[now*2+1], A[now*2+1], B[now*2+1], t[now], k[now]);
circ2(t[now*2], k[now*2], t[now*2], k[now*2], t[now], k[now]);
circ2(t[now*2+1], k[now*2+1], t[now*2+1], k[now*2+1], t[now], k[now]);
k[now]=0; t[now]=-inf;
}
}
void add(int now, int l,int r,int x,int y,int K) {
if(l>=x&&r<=y) {
circ2(t[now], k[now], t[now], k[now], -inf, K);
circ3(A[now], B[now], A[now], B[now], -inf, K);
return;
}
if(l>y||r<x)return;
int mid=(l+r)>>1;
pushdown(now);
add(now*2,l,mid,x,y,K); add(now*2+1,mid+1,r,x,y,K);
circ1(A[now],B[now],A[now*2],B[now*2],A[now*2+1],B[now*2+1]);
}
void aft(int now) {
//历史和行为
circ2(t[now], k[now], t[now], k[now], 0, 0);
circ3(A[now], B[now], A[now], B[now], 0, 0);
return;
}
int que(int now,int l,int r,int x,int y){
if(l>=x&&r<=y){return B[now];}
if(l>y||r<x)return -inf;
int mid=(l+r)>>1;
pushdown(now);
return max(que(now*2,l,mid,x,y),que(now*2+1,mid+1,r,x,y));
}
}sgt;
struct node {
int l, r; int mid; //外层的 size 是 mid - l; r - mid + 1.
vector<vector<query>> lq, rq; //在左边的询问和右边的询问,得到的答案加上 tag 和 ans[id] 取 max
vector<vector<line>> la, ra; //区间加
vector<line> qjadd; // 全局 add
};
// int eee = 0;
struct timetree {
node timeqj[200010];
void build(int now, int l, int r) {
timeqj[now].l = l; timeqj[now].r = r;
timeqj[now].mid = (l + r) >> 1;
timeqj[now].lq.resize(timeqj[now].mid - l + 2 + 1); timeqj[now].la.resize(timeqj[now].mid - l + 2 + 1);
timeqj[now].rq.resize(r - timeqj[now].mid + 1 + 1); timeqj[now].ra.resize(r - timeqj[now].mid + 1 + 1);
if(l == r) return;
int mid = (l + r) >> 1;
build(now * 2, l, mid); build(now * 2 + 1, mid + 1, r);
}
void addin(int now, int l, int r, qj x) {
int mid = (l + r) >> 1;
int lo = mid, ro = mid + 1; // 时间为 t 的在左边的编号是 mid - t, 右边是 t - mid - 1
if(x.l <= mid) {
timeqj[now].la[lo - min(mid, x.r) + 1].push_back({x.x, x.y,x.k});
timeqj[now].la[lo - (x.l - 1) + 1].push_back({x.x, x.y, -x.k});
if(l != r) {
if(x.l == l && x.r >= mid) timeqj[now * 2].qjadd.push_back({x.x, x.y, x.k});
else addin(now * 2, l, mid, {x.l, min(mid, x.r), x.x, x.y, x.k});
}
}
if(x.r >= mid + 1) {
timeqj[now].ra[max(mid + 1, x.l) - ro + 1].push_back({x.x, x.y,x.k});
timeqj[now].ra[x.r + 1 - ro + 1].push_back({x.x, x.y, -x.k});
if(l != r) {
if(x.r == r && x.l <= mid + 1) timeqj[now * 2 + 1].qjadd.push_back({x.x, x.y, x.k});
else addin(now * 2 + 1, mid + 1, r, {max(mid + 1, x.l), x.r, x.x, x.y, x.k});
}
}
}
void queryin(int now, int l, int r, xw x, int id) {
int mid = (l + r) >> 1; assert(x.l >= l && x.r <= r);
int lo = mid, ro = mid + 1;
if(x.l >= l && x.r <= r && x.l <= mid + 1 && x.r >= mid) {
if(x.l <= mid)timeqj[now].lq[lo - x.l + 1].push_back({x.x, x.y, id});
if(x.r >= mid + 1) timeqj[now].rq[x.r - ro + 1].push_back({x.x, x.y, id});
return;
}
else if(x.r <= mid) queryin(now * 2, l, mid, x, id);
else queryin(now * 2 + 1, mid + 1, r, x, id);
}
void dfs(int now, int l, int r) {
//注意要先 - 再 +,这里满足了
//处理左半边区间,右半边区间
if(l == r && n != 1) return;
int delta = sgt.B[1];
sgt.add(1, 1, n, 1, n, delta);
int llen = timeqj[now].mid - timeqj[now].l + 2;
for(line it : timeqj[now].qjadd) sgt.add(1, 1, n, it.l, it.r, it.k);
f(i, 1, llen) {
for(line it : timeqj[now].la[i]) {
sgt.add(1, 1, n, it.l, it.r, it.k);
}
sgt.aft(1);
for(query it : timeqj[now].lq[i]) {
int tmp = sgt.que(1, 1, n, it.l, it.r);
cmax(ans[it.id], tmp - delta);
}
}
sgt.add(1, 1, n, 1, n, -delta);
int rlen = timeqj[now].r - timeqj[now].mid + 1;
delta = sgt.B[1];
sgt.add(1, 1, n, 1, n, delta);
f(i, 1, rlen) {
assert((int)timeqj[now].ra.size() > i);
assert((int)timeqj[now].rq.size() > i);
for(line it : timeqj[now].ra[i]) {
sgt.add(1, 1, n, it.l, it.r, it.k);
}
sgt.aft(1);
for(query it : timeqj[now].rq[i]) {
int tmp = sgt.que(1, 1, n, it.l, it.r);
cmax(ans[it.id], tmp - delta);
}
}
sgt.add(1, 1, n, 1, n, -delta);
int mid = (l + r) >> 1;
if(l != r) {dfs(now * 2, l, mid); dfs(now * 2 + 1, mid + 1, r);}
for(line it : timeqj[now].qjadd) sgt.add(1, 1, n, it.l, it.r, -it.k);
}
}tt;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m1 >> m2;
tt.build(1, 1, n);
f(i,1,m1) {
qj x; cin >>x.l>>x.x>>x.r>>x.y>>x.k;
tt.addin(1, 1, n, x);
}
f(i,1,m2){
xw x; cin >>x.l>>x.x>>x.r>>x.y;
tt.queryin(1, 1, n, x, i);
}
tt.dfs(1, 1, n);
f(i,1,m2)cout<<ans[i]<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at 16:51
finish debugging at h:mm
*/
分段检查:线段树先写好,然后检查完线段树再去写分治。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具