莫队
算法介绍
如果有一个序列上的多个区间询问,并且可以离线,且某区间 \([l, r]\) 推到 \([l + 1, r], [l, r + 1], [l - 1, r], [l, r - 1]\) 是比较容易的,那么可以使用一种较好的排序询问方式,使得总端点位移次数达到一个较小的值。
这种排序方式是:考虑对序列分块,对于两个区间,如果块不同,那么按块排序,否则按 \(r\) 排序。
考虑这个位移次数。对于 \(l\),最坏情况是在块内左右横跳,\(S^2 \times \cfrac{n}{S}\) 的次数,并且这一部分常数小,跑不满。对于 \(r\),每块内只会从左到右跑一次,\(\cfrac{n}{S} \times n\) 的次数。
将其平衡,那么 \(S\) 取 \(\sqrt n\) 可以达到理论的界 \(n \sqrt n\)。实际上由于常数可以将 \(S\) 调大一些。至于增加和删除操作所花费的时间,乘到总时间里即可。块长可以灵活调整,如果增删时间不同,也可以改块长。
有一个优化一倍常数的方式:对奇数标号的块,\(r\) 从小到大排序,否则从大到小排序。
实现上,通常先扩张区间然后缩小区间,也就是先进行 \(r++, l--\)。然后注意缩小区间的时候要先删除当前指针位置然后移动指针。
树上莫队
考虑树上括号序(进出的时候加入一次括号序)。对于询问:路径 \((s, t)\),我们分两种情况将其转为括号序上的询问:
-
\(s\) 是 \(t\) 的祖先。那么 \(tail_t \rightarrow tail_s\)。
-
两者没有祖先关系,这代表两方括号序上区间不交,假设 \(s\) 在 \(t\) 前面。那么 \(tail_s \rightarrow head_t\)。
括号序内,出现两次的是不在路径上的子树,不做贡献。
如果询问的是点的相关信息,那么注意第二种情况并没有计算入 lca 的贡献。如果询问的是边的相关信息,考虑所有边都放到儿子的位置,这样做就是完全正确的了。
回滚莫队
对于并不支持删除操作的情况,可以这样做:
- 预处理每一个 \(l\) 到其块末尾 \(tail\) 的信息。
- 对于某一块内的询问,将 \(r\) 从小到大排序。对于块内的 \(r\) 暴力求解,对于块外的 \(r\) 维护 \([tail + 1,r]\) 的信息,然后和 \([l, tail]\) 合并。
分析时间复杂度:
- 预处理的时候,每一块从右往左每次需要复制和处理一个长度为 \(1, 2, ..., S\) 的块,总时间复杂度 \(O(nS)\)。
- 询问的时候,暴力的时间复杂度是 \(O(q_1S)\)。
- 其他的时间复杂度是 \(O(n\cfrac{n}{S})\)。
容易发现理论上最优复杂度依然是 \(O(n \sqrt n)\)。
对于“合并”的理解:有两种形式,一种是直接一个一个往左扫,这时候空间是很小的,不需要存块后缀信息,而复杂度是依然正确的,就是每次询问加了 \(O(\sqrt n)\)。还有一种就是保存后缀信息,并且合并。如果可以在 \(O(1) \sim O(\sqrt n)\) 的时间复杂度内完成合并,那么也是可以的,可能可以卡时间常数,但是空间复杂度变成了 \(O(n \sqrt n)\)(假设后缀信息的复杂度正比于其长度)。不过目前看好像大多数情况是第一种比较好。
同样,也可以是不支持插入的。(有的题就是删除更好做,用链表维护和 set 里插入的区别这样)。大概就是 \(r\) 从大到小排,然后某一块开始的时候取块首到 \(n\),然后删两头这样。
joisc 2023 Day 3 C
【题意】
给定一个 \(n\) 个点的树,有一个 \(m\) 个数的序列 \(a\),\(q\) 次询问,每次求从任意一个点开始走一条树上路径经过 \(a_l \sim a_r\) 中所有点的话,路径上经过至少一次的点数最少是多少。
【分析】
容易发现这题是求区间上点的虚树大小。
方法 1:
考虑莫队。
考虑加入某一个数。
如果直接加入并维护虚树,需要找到虚树上其最近祖先,二分线段树可以做到 \(\log^2\),但是显然过不去。
考虑虚树性质,可以 dfn 排序然后计算相邻两两距离之和。
如果使用不删除莫队,加入 \(\log\),用 set 维护,但是注意到这个题只需要查询 kth 的 rank,可以使用权值树状数组代替 set,具体这么做:
- 查询 rank:直接查询前缀和即可。
- 查询 kth:考虑树状数组上二分。
树状数组一种二分方式是直接模拟线段树二分(不同之处在于一个能求区间 kth,一个能求全局 kth)
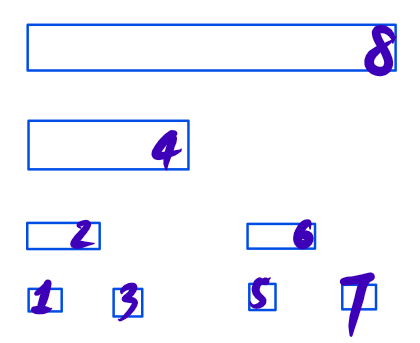
树状数组(记为 \(a\))长这样,我们考虑初始令 \(now = n, digit = \log_2 n - 1, k = k\)。这个 \(digit\) 的意思就是在哪一位。比如 \(digit = 2\) 就是在第三层(\(4\) 那一层)
如果 \(a_{now - 2^{digit}} \ge k\) 那么向左边走(\(now -= 2^{digit}\));否则向右边走(\(k -= a_{now - 2^{digit}}\))。不管往哪边走,\(digit--\)。
注意 \(n\) 要补到 \(2^n\),这个空间上要注意一下,但是由于后面的都是 \(0\),是不需要做其他事情的。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍!
//use std::array.
int n;
struct szsz {
int a[100010];
int lowbit(int x) {return x & -x;}
void add(int x, int k) {
while(x <= n) {
a[x] += k;
x += lowbit(x);
}
}
int rnk(int x) {
int res = 0;
while(x > 0) {
res += a[x];
x -= lowbit(x);
}
return res;
}
int kth(int k) {
int newn = 1 << ((int)log2(n - 1) + 1);
int now = newn, dig = log2(newn) - 1;
while(dig >= 0) {
if(a[now - (1 << dig)] >= k) {
now -= (1 << dig);
}
else {
k -= a[now - (1 << dig)];
}
dig--;
}
return now;
}
}tr;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> n; int q; cin >> q;
f(i, 1, q) {
int op; cin >> op;
if(op == 1){int x, k; cin >> x >> k; tr.add(x, k);}
else if(op == 2) {int x; cin >> x; cout << tr.rnk(x) << endl;}
else {int x; cin >> x; cout << tr.kth(x) << endl;}
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at h:mm
finish debugging at h:mm
*/
上面的这份代码,在点有权值的情况下,rnk 出来的是最大 rnk,kth 就是 kth。
于是我们成功把 set 改成了常数十分小的权值树状数组。这样 \(O(n \sqrt n \log n)\) 就可以在 4s 内卡过啦!(确信)
方法 2:
我们考虑把不删除改成不加入。(回滚莫队不仅能做不删除,也可以做不加入,具体方法就考虑某一块先计算 \(head \sim n\) 的答案,然后移动两边的指针)
这样做有什么好处呢?我们删除的时候直接用链表删除即可。(之前小瞧了这个数据结构,但是确实很有用)这样不用维护一棵平衡树,是 \(O(1)\) 的。考虑每一块插入过程。可以对 \(O(n)\) 长度的数组直接排序。暴力插入还是带一个 \(\log\),但是我们可以从右往左进行。这样做,这部分复杂度直接变成 \(O(n \log n)\),那么整体复杂度就是纯根号的。
方法 3:
考虑虚树的另一种形式:虚树根到原树根的一条链加上原树根到点集中所有点的并。
首先链是好求的,就一个区间 lca,这里不说了。重点是并怎么算。注意到这里就转化为了到根的链上问题了。如果不知道接下来干什么,接着想。
考虑扫描线的第二种形式,扫 \(r\),维护所有 \(l\) 的答案。考虑二维数点那个做法,维护最后一次出现位置。可以启发到这题上。注意到一个 \(r\) 是给 \(r\) 到 \(1\) 的链上这些点全部加入一次虚树,那么我们考虑维护时间戳,也就是每一个点是什么时候加入的虚树。
发现这个全部加入类似颜色段均摊处理的东西,考虑树剖之后是 \(\log\) 段连续段,这意味着每次扫描线右端点动了的时候只会插入 \(\log\) 段区间,所以这部分的时间复杂度是 \(O(\log^2 )\) 的。
考虑查询怎么做。额外维护一个权值树状数组拿来查询 rank。只需要实时维护颜色为某一个数的区间总大小即可。查询部分的时间复杂度是 \(O(\log)\) 的。
分几步:
- 树剖预处理。
- 扫描线,预先把所有区间打到 \(r\) 上。每次 \(r\) 动的时候,沿着 \(1 \sim c_r\) 的链走,更新颜色段,并在树状数组里更新。
- 处理查询,在树状数组里查询即可。树状数组支持 rank。
总时间复杂度 \(O(n + n \log^2 n + q \log n)\)。
三维莫队
给定 \((i_n, j_n, k_n)\) 数组,长度为 \(n\),值域 \([1, n]\),数据随机,求一组排列,使得下式比较小:
考虑对 \(x, y\) 两个维度分块,令 \(z\) 递增。由于数据随机,可以认为是均匀的。
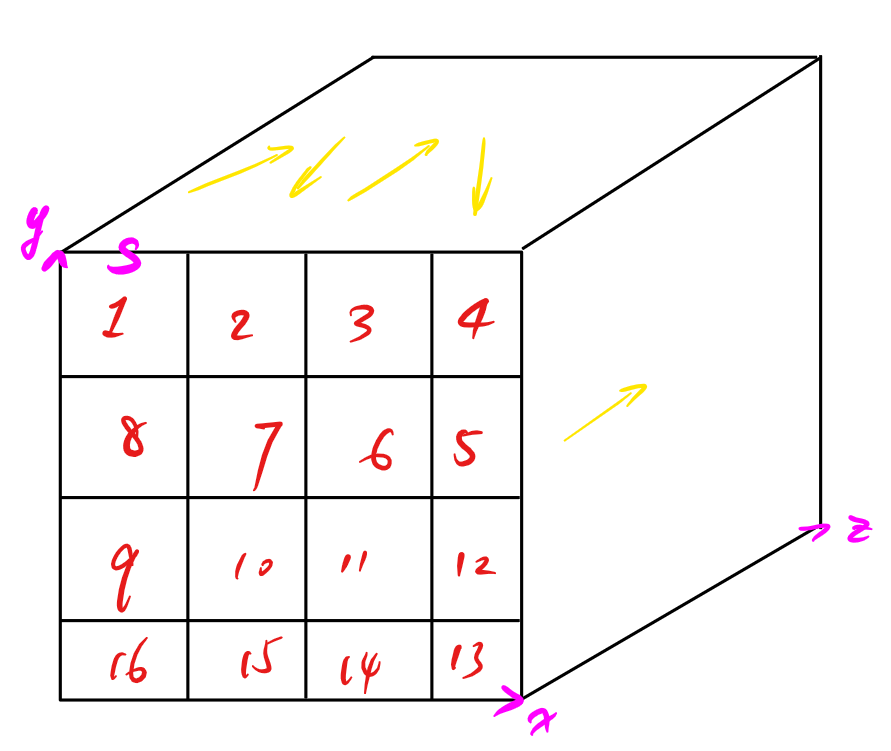
考虑块长为 \(S\),那么块数 \(O(\cfrac{n^2}{S^2})\)。\(z\) 端点移动距离 \(O(\cfrac{n^2}{S^2} \times n)\),\(x,y\) 端点移动距离 \(O(nS)\)。令其根号平衡可得 \(S = n^{\frac{2}{3}}\),算出来答案 \(O(n^{\frac{5}{3}})\)。


