树链剖分

介绍

解决树上问题的时候，对于路径问题我们会想到树分治、启发式合并。对于子树问题我们会想到在 dfs 序上转化为序列问题方便维护。

那么对于路径问题，能不能也转化为序列问题？

可以的。

这就是树链剖分在做的事情：把一棵树划分为若干段 dfn 连续的区间，使得某一个路径可以被拆分为 \(O(\log n)\) 个 dfs 序区间。（为了方便这里把拆出来的叫区间，原来的路径叫链）

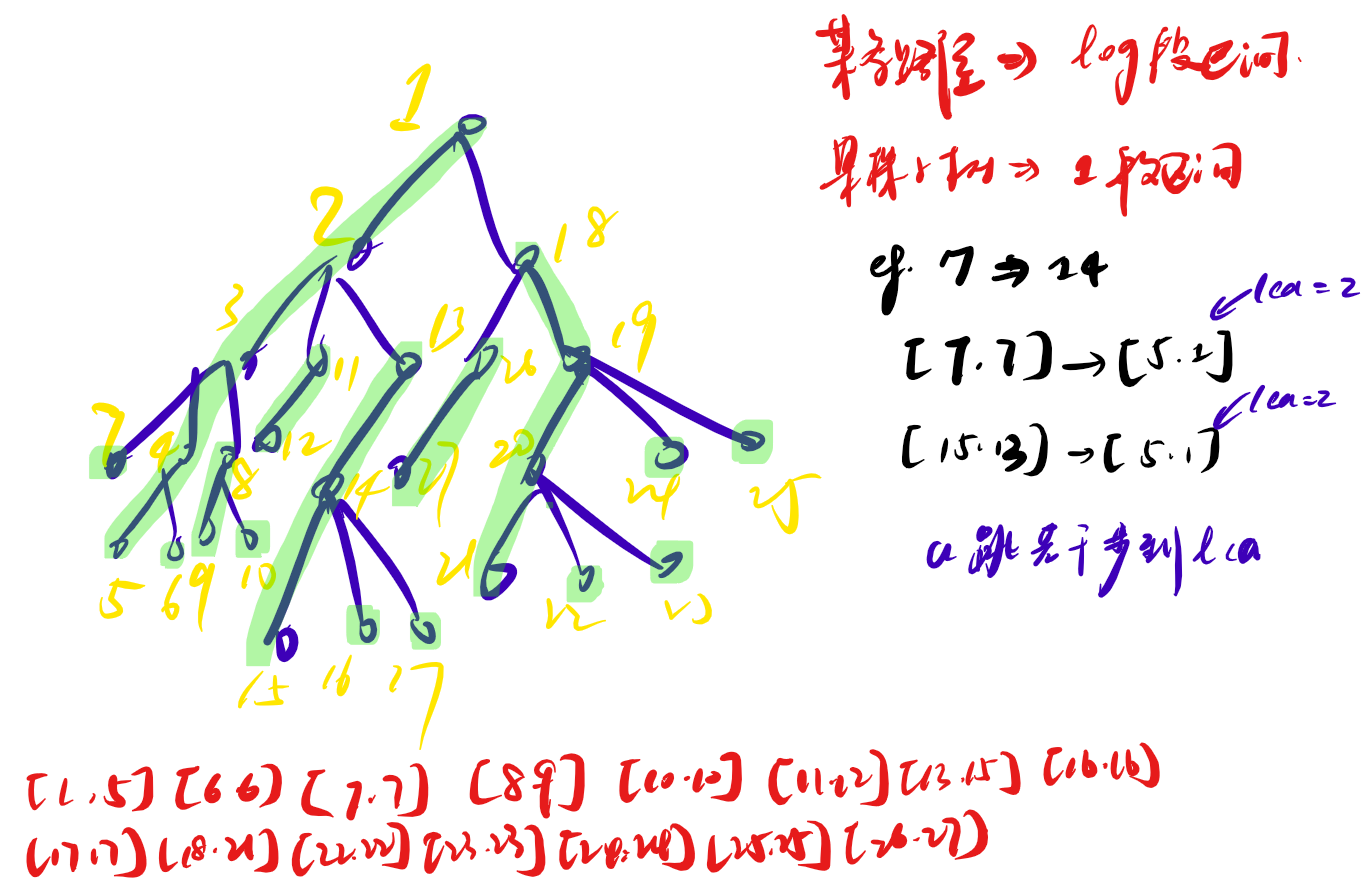
虽然一开始给你的树不一定能够做到这一点，但是我们对 dfs 的顺序进行改变，可以做到这一点。考虑每次 dfs 到一个节点之后优先向其重儿子去遍历。

我们来证明一下上面的两个结论正确性。

首先，一棵树被划分为段 dfn 连续的区间：显然，某一个节点和父亲不连续说明它不是重儿子，于是不会被分到一起。

其次，一条路径被划分为 \(O(\log n)\) 段链：首先考虑某个点到根节点的路径。考虑现在有一个从 \(1\) 开始朝着另一端行走的人，它跳到另一个区间上花费 \(1\) 的代价。考虑其子树大小，每次一定减去至少一半。因此一共花费 \(O(\log n)\) 的代价。再考虑一般的路径，显然和其同阶。

考虑我们如何找到这些拆成的区间。我们有初始节点 \((x,y)\) 代表链的两端。然后不断选择所在区间深度较大的那一个点（假设是 \(x\)），找到链顶 \(top\)，对 \((top, x)\) 区间做贡献，然后 \(x\) 跳到 \(top.fa\)。注意区间深度指的是根节点到这条链要穿过几条链，因为如果使用的是点的深度，那么上图的 \(5 \rightarrow 8\) 因为 \(5\) 深度较大要跳，但是它已经不能再跳了。

伪代码：

void gx(int x, int y) {
	while(1) {
		if(x.belong.deep < y.belong.deep) swap(x,y);
		if(x.belong != y.belong) {
			update(x.belong.top, x); //dfn 连续段
			x = fa[x.belong.top];
		}
		else break;
	}
	if(x.depth > y.depth) swap(x, y);
	update(x, y);
}

如何进行树剖

考虑需要维护什么。

• 子树大小 -> 重儿子。
• dfs 序，以及每个 dfs 序对应什么节点。
• 每个节点属于什么链上。
• 链顶和底。
• 每条链的深度。
• 点的深度。
• 点的父亲。

做两次 dfs 进行维护。

第一次 dfs 维护什么：

• 子树大小 -> 重儿子。
• 点的深度。
• 点的父亲。

第二次 dfs 维护什么：

• dfs 序，以及每个 dfs 序对应什么节点。
• 每个节点属于什么链上。
• 链顶和底（但是我们发现好像不太需要维护链底）。
• 每条链的深度。

模板题：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr  << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
    string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; } 
    reverse(s.begin(), s.end()); cerr << s << endl; 
    return;
}
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍！
int n,m,root,p;
int a[200100],sgt[800100],tag[800100]; vector<int>t[200100];
int dfn[200100],rnk[200100],fa[200100],top[200100],dep[200100],deep[200100];
int hea[200100],sz[200100],dcnt,en[200100];
void dfs1(int now) {
    //get sz, hea, dep, fa
    sz[now]=1; dep[now]=dep[fa[now]]+1; int mx=0,mxn=0;
    for(int i:t[now]) {
        if(i==fa[now])continue;
        else {fa[i]=now; dfs1(i); sz[now]+=sz[i]; if(mx<sz[i]){mx=sz[i];mxn=i;}}
    }
    hea[now]=mxn;
}
void dfs2(int now) {
    dfn[now]=++dcnt; rnk[dcnt]=now;
    if(hea[now]!=0){
        deep[hea[now]]=deep[now]; top[hea[now]]=top[now]; dfs2(hea[now]);
    }
    //get dfn, top, deep, rnk
    for(int i:t[now]){
        if(i!=fa[now]&&i!=hea[now]){deep[i]=deep[now]+1; top[i]=i;dfs2(i); }
    }
    en[now]=dcnt;
}
void pushdown(int now,int l,int r){
    if(tag[now]){
        int mid=(l+r)>>1;
        sgt[now*2]+=(mid-l+1)*tag[now]%p;tag[now*2]+=tag[now]%p;
        sgt[now*2+1]+=(r-mid)*tag[now]%p;tag[now*2+1]+=tag[now]%p;
        sgt[now*2]%=p;sgt[now*2+1]%=p;tag[now*2]%=p;tag[now*2+1]%=p;
        tag[now]=0;
    }
}
void build(int now,int l,int r) {
    if(l==r){sgt[now]=a[rnk[l]]; return;}
    int mid=(l+r)>>1;
    build(now*2,l,mid);build(now*2+1,mid+1,r);
    sgt[now]=sgt[now*2]+sgt[now*2+1];
}
void add(int now,int l,int r,int x,int y,int k) {
    // cerr<<"add "<<now<<" "<<l<<" "<<r<<" "<<x<<" "<<y<<" "<<k<<endl;
    if(l>=x&&r<=y){
        sgt[now]+=(r-l+1)*k%p;tag[now]+=k;sgt[now]%=p;tag[now]%=p; 
        return;
    }
    if(l>y||r<x){return;}
    int mid=(l+r)>>1; pushdown(now,l,r);
    add(now*2,l,mid,x,y,k); add(now*2+1,mid+1,r,x,y,k);
    sgt[now]=sgt[now*2]+sgt[now*2+1];
}
int get(int now,int l,int r,int x,int y) {
    // cerr<<"get "<<now<<" "<<l<<" "<<r<<" "<<x<<" "<<y<<endl;
    if(l>=x&&r<=y){return sgt[now];}
    if(l>y||r<x){return 0;}
    int mid=(l+r)>>1; pushdown(now,l,r);
    return (get(now*2,l,mid,x,y) + get(now*2+1,mid+1,r,x,y)) % p;
}
void addc(int x,int y,int z) {
    while(1) {
        if(top[x]!=top[y]){
            if(deep[x] < deep[y])swap(x,y);
            add(1,1,n,dfn[top[x]],dfn[x],z); x=fa[top[x]];
        }   
        else break;
    }
    if(dep[x]>dep[y])swap(x,y);
    add(1,1,n,dfn[x],dfn[y],z);
}
void quec(int x,int y){
    int res=0;
    while(1) {
        if(top[x]!=top[y]){
            if(deep[x] < deep[y])swap(x,y);
            res+=get(1,1,n,dfn[top[x]],dfn[x]); x=fa[top[x]]; res%=p;
        }   
        else break;
    }
    if(dep[x]>dep[y])swap(x,y);
    res+=get(1,1,n,dfn[x],dfn[y]); res %= p;
    cout<<res%p<<endl;
}
void adds(int x,int z){add(1,1,n,dfn[x],en[x],z);}
void ques(int x){cout<<get(1,1,n,dfn[x],en[x])<<endl;}
int qcnt=0;
void query() {
    // cerr << "query number #" << ++qcnt << endl;
    int op;cin>>op;
    if(op==1){int x,y,z;cin>>x>>y>>z;addc(x,y,z);}
    else if(op==2){int x,y;cin>>x>>y;quec(x,y);}
    else if(op==3){int x,z;cin>>x>>z;adds(x,z);}
    else if(op==4){int x;cin>>x;ques(x);}
}
void debug() {
    f(i,1,n){
        cerr<<i << " 's info: "<< "father = " << fa[i]<<", top = " << top[i]<<", dep = "<<dep[i]<<", deep = " << deep[i]<<", dfn = " << dfn[i] << ", en = " << en[i]<<", hea = " << hea[i] << endl;
    }
}
signed main() { 
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //freopen();
    //freopen();
    //time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    cin>>n>>m>>root>>p;
    f(i,1,n)cin>>a[i];
    f(i,1,n-1){int u,v;cin>>u>>v;t[u].push_back(v);t[v].push_back(u);}
    top[root]=root; dfs1(root); dfs2(root);  build(1,1,n); 
    f(i,1,m){query();}
    //time_t finish = clock();debug();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}
/*
2023/3/10
start thinking at 


start coding at 14:52
finish debugging at 15:55
*/