多项式相关

多项式，就是提供了一个代数手段解决问题。——rsy

1 多项式的次数

1.1 差分法

考虑一个数列 $\{a_n\}$。其是一个关于 $n$ 的 $v$ 次多项式。

对数列做 $d$ 阶差分之后变成一个非零常数数列（所有 $a_i$ 都是一个固定的非零常数）等价于多项式的次数为 $d$。

证明：

考虑 $a_n = \sum \limits_{i = 1}^v w_i n^i$。
那么 $a_n - a_{n-1}$ 的 $v$ 次项相减是这样的：

$$w_vn^v - w_v(n-1)^v$$

注意到 $n^v$ 系数清零。因此多项式降低一次。

归纳即可。

（对于 $n$ 你发现可以代入一些数字，但是其是多项式主元，而常数和 $n$ 无关的就不在次数里了）

CF622F The Sum of the k-th Powers

【题意】
求 $\sum \limits_{i = 1}^n i^k$。

$n \le 10^9, k \le 10^6$。

【分析】

为什么这个式子是 $k+1$ 次多项式？
考虑 $a_1 = 1^k, a_2 = 1^k + 2^k ...$
差分一次之后变成 $1^k, 2^k, ..., n^k$ 显然为 $k$ 次多项式。
证完了。

然后就可以插值。计算 $i^k$ 可以线性筛，因为它是完全积性函数。

时间复杂度 $O(k)$。

CF1817C Similar Polynomials

【题意】
给定两个多项式 $f(x)$ 和 $g(x)$，其中 $g(x) = f(x + t)$。给定多项式的次数 $d$ 以及 $0 \sim d$ 处的点值，求 $t$。

【分析】
考虑 $d-1$ 次差分之后会变成一个一次函数（等差数列）。$\Delta^{d-1} f$ 放到坐标轴上，往左平移 $t$ 个单位，就是 $\Delta^{d-1} g$ 了。

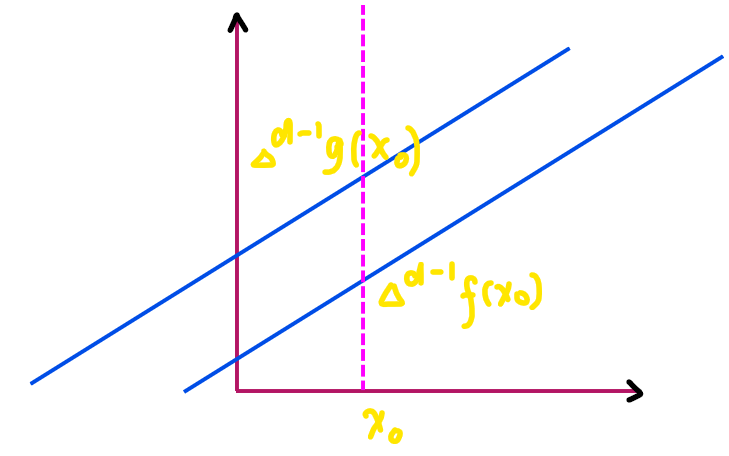
代数形式是：$ax + b \rightarrow a(x+t)+b$，$x$ 固定的情况下差值为 $at$，于是除以 $a$（斜率）即可。

你如果换成别的次数（大于 $0$）也能算，但是解的就是高次方程了。

$d-1$ 阶差分怎么做：

$$\begin{matrix} a_0 & a_1 & a_2 & a_3 & a_4\\ & a_1-a_0 & a_2-a_1 & a_3-a_2 & a_4-a_3 \\ & & a_2-2a_1+a_0 & a_3-2a_2+a_1 & a_4-2a_3+a_2 \\ & & & a_3-3a_2+3a_1-a_0 &a_4-3a_3+3a_2-a_1 \end{matrix}$$

也即 $\Delta^d f_i = \sum \limits_{j = 0}^d a_{i-j} \times \dbinom{d}{j} \times (-1)^{i-j}$。

斜率是什么？$\Delta^{d-1} f_d - \Delta^{d-1} f_{d-1}$。

CF1832E Combinatorics Problem

【题意】
给定 $n, k$ 和数组 $a_1, ..., a_n$，求出 $\{b_n\}$ 使得：

$$b_i = \sum \limits_{j = 1}^i \dbinom{j}{k}a_{i-j+1} \bmod 998244353$$

$1 \le n \le 10^7, 1 \le k \le 5$
【分析】
我们列出每一项的展开形式：

$$\begin{array}{l} b_1 = \dbinom{1}{k}a_1 \\ b_2 = \dbinom{2}{k}a_1 + \dbinom{1}{k}a_2 \\ b_3 = \dbinom{3}{k}a_1 + \dbinom{2}{k}a_2 + \dbinom{1}{k}a_3 \\ ... \end{array}$$

对于多项式 $f_n = \dbinom{n}{k}$，其是一个 $k$ 次多项式，因为它等于 $\cfrac{n_{[k]}}{k!}$。

那么我们如果对数列 $b_1, b_2, ...$ 做 $k$ 阶差分会变成常数。打表不难发现常数为 $1$。

于是我们构造：

$$\begin{array}{l} c_1 = a_1 \\ c_2 = a_1 + a_2 \\ c_3 = a_1 + a_2 + a_3 \\ ... \end{array}$$

再对 $c$ 数组做 $k$ 阶差分即可。时间复杂度 $O(nk)$。

另解：
考虑 $\dbinom{i}{j}= \dbinom{i-1}{j-1} + \dbinom{i-1}{j}$，那么如果令 $B_{i,j}$ 表示 $k=j$ 的时候 $b_i$ 是多少，那么 $B_{i,j} = B_{i-1,j-1} + B_{i-1,j} + \dbinom{1}{j}a_i$。可以递推得到，时间复杂度也是 $O(nk)$。