FFT

复数

复数的代数表示：\(a+bi\)，定义 \(i^2=-1\)。

四则运算：

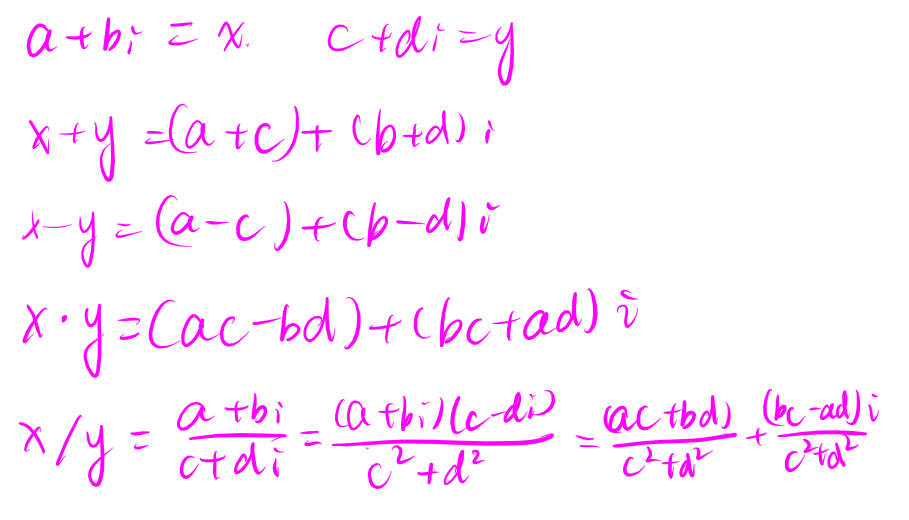
其中 \(a+bi\) 和 \(a-bi\) 是共轭复数，其乘积为 \(a^2+b^2\)。

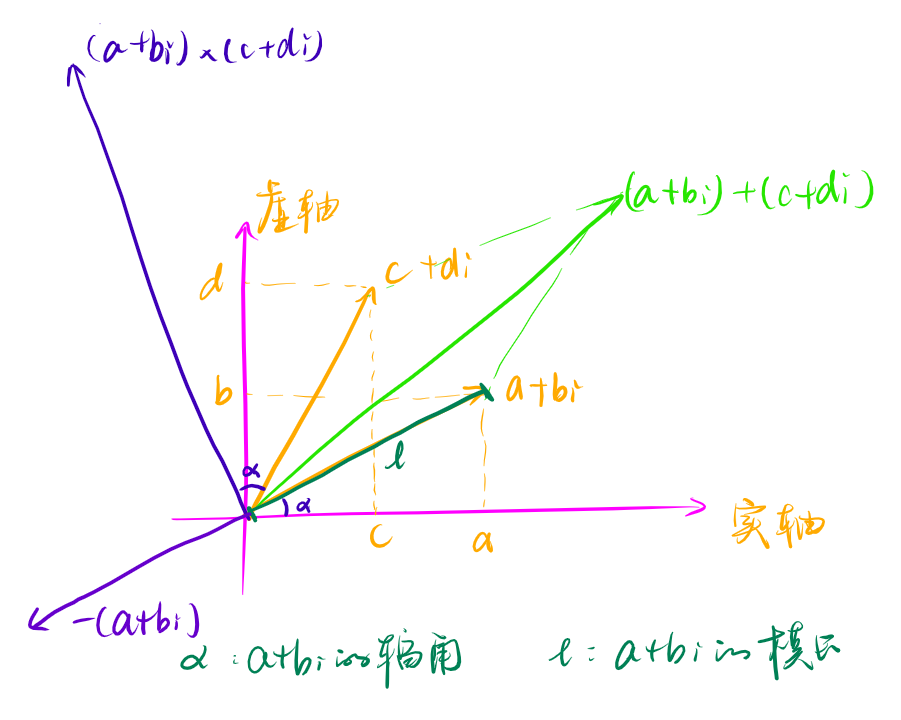
复数的几何表示：实轴和虚轴两个轴组成平面直角坐标系，构成复平面，一个复数就是复平面上的一个向量。

相反数、加法、乘法运算如下图所示。

乘法运算的性质：幅角相加，模长相乘。证明：

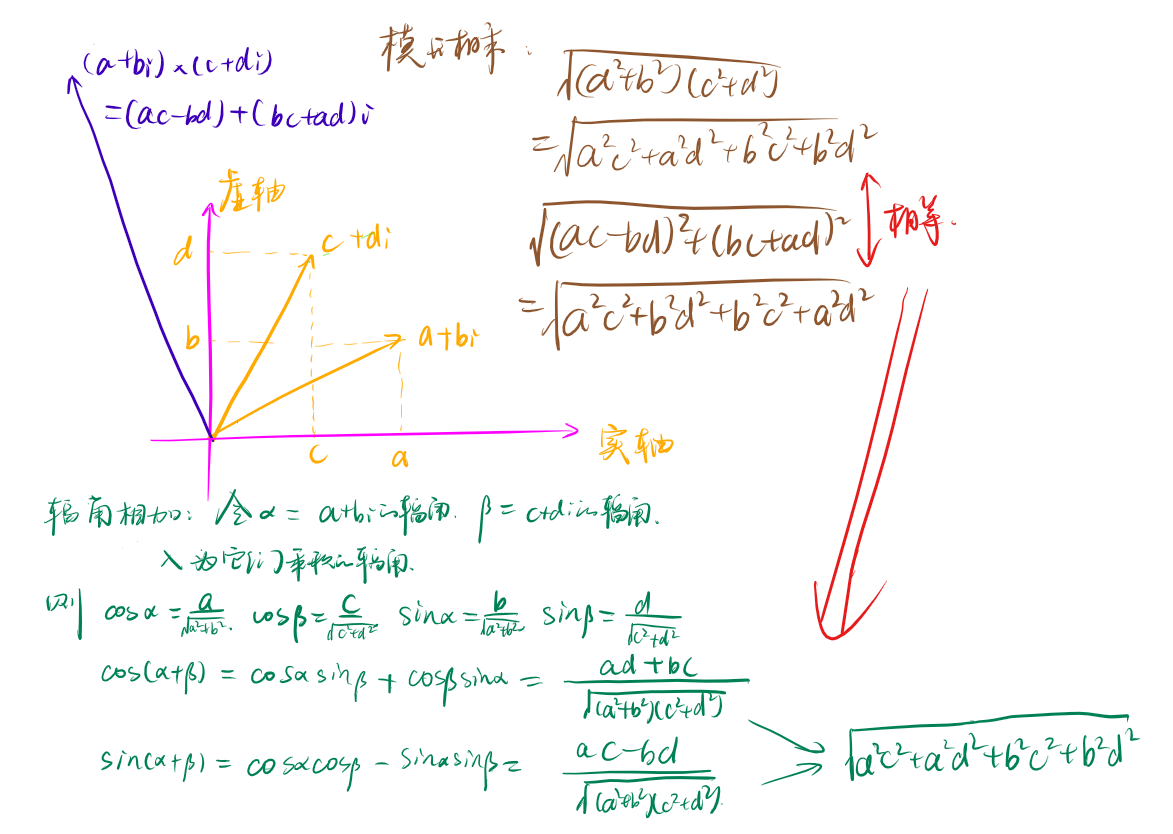
（这个角的 \(\sin\) 值和 \(\cos\) 值都等于两个向量乘积的，因此可以确定这个角）

单位根

定义 \(n\) 次单位根为方程 \(x^n = 1\) 的解，记为 \(\omega_n\)。根据代数基本定理解有 \(n\) 个，给它们编号，第 \(i\) 个记为 \(\omega_n^i\)。都是复数。考虑它们在复平面上的位置：都在单位圆上。理由是，对于模长大于 \(1\) 的向量，其 \(n\) 次方模长也大于 \(1\)，小于类似。因此只有等于的才可能做单位根。

考虑其幅角。注意到幅角为 \(\alpha\) 的角的 \(n\) 次方幅角为 \(n \alpha\)，因此幅角为 \(\cfrac{k}{n}\) 的向量可以是单位根。我们在复平面内幅角任意 \(+ 2\pi\) 得到的结果是同一个复数，因此我们只考虑角度在 \(0 \sim 2 \pi\) 之间的角。它们在圆上均匀排列，因此顺时针给它们标号，如下图所示：

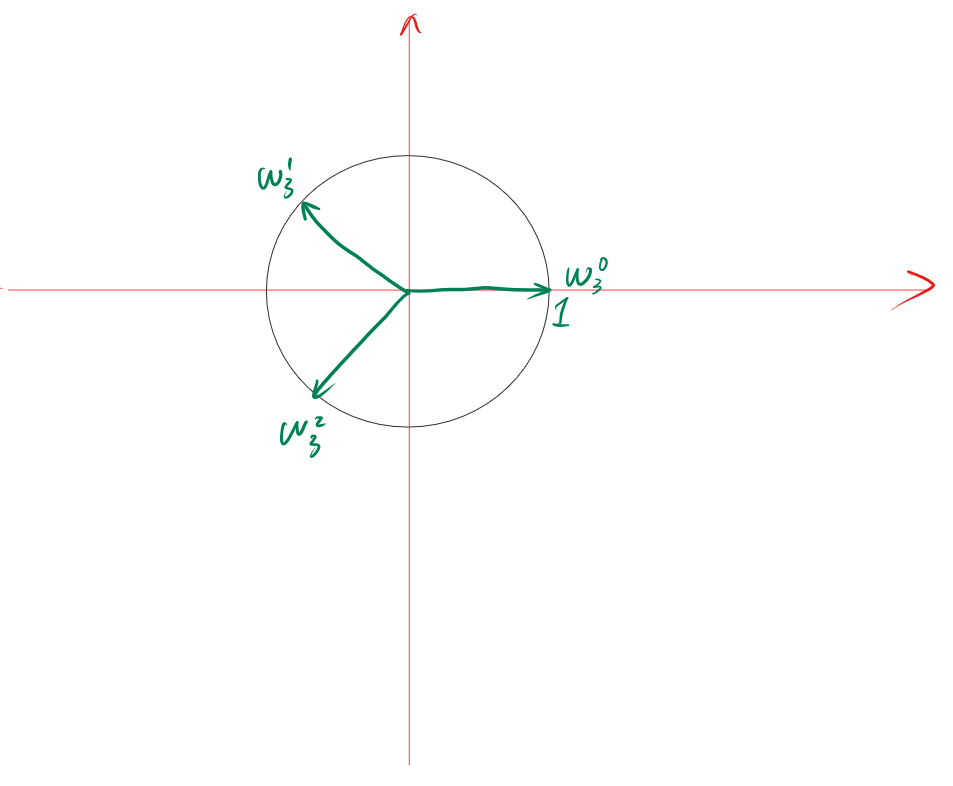
性质：

FFT

对两个多项式做乘法。

记多项式 \(F(x)\) 的 \(k\) 次项系数为 \(F[k]\)，考虑 \((F \times G)[k] = \sum \limits_{i = 0}^k F[i]G[k-i]\)。相当于对于系数是做了个卷积。

考虑另一个方面，\(n+1\) 个点确定一个 \(n\) 次多项式。找到 \(F,G\) 的点值，相乘，然后插值，可以得到一个多项式乘法的方式。当 \(x\) 是形式主元的时候，是一个求解加法卷积的方法。

这要选择 \(2n\) 个点，但是每一个点值的计算都是 \(O(n)\) 的。有没有方法加速？

傅里叶的 FFT 做到了加速，将其降为 \(O(n \log n)\)，运用了分治的方式。

怎么做到的呢？考虑 \(F(x) = \sum \limits_{i = 0}^{n-1} F[i]x^i\)，其中 \(n\) 是多项式的项数，是偶数。把它分成一个奇函数和一个偶函数并且重新赋 \(x\)：\(Fl(x) = F[0]x^0+F[2]x^1+...+F[n-1]x^{\frac{n}{2}-1}\) 和 \(Fr(x) = F[1]x^0+F[3]x^1+...+F[n]x^{\frac{n}{2}-1}\) 两部分。那么 \(F(x) = Fl(x^2) + x Fr(x^2)\)。
现在代入单位根：

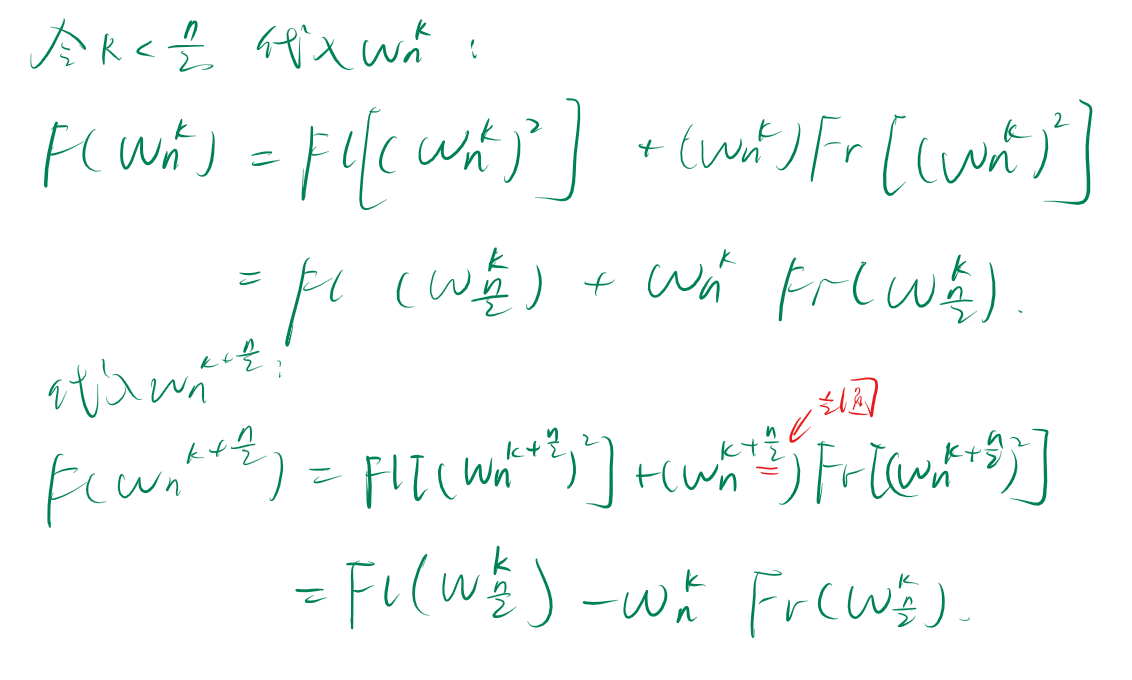
我们发现问题被划分为了两个子问题：\(Fl(w_{\frac{n}{2}}^k),Fr(w_{\frac{n}{2}}^k)\)。

（怎么想到的呢？是因为有奇偶性的函数得到点值可以得到其相反数的点值。并且单位根很有性质，于是用了它）

合并的时候，是 \(O(1)\) 的。

因此 \(T(n) = 2T(\frac{n}{2}) + O(1)\)，总时间复杂度 \(O(n \log n)\)。

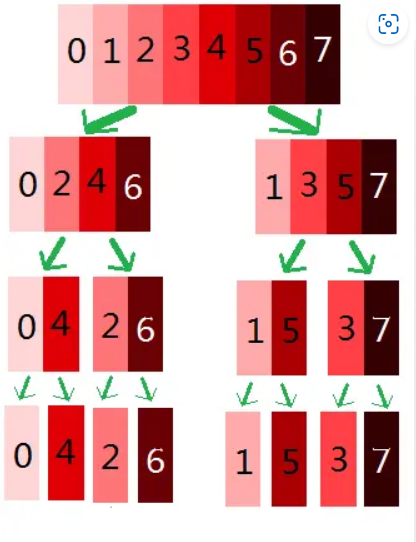
这个单位根比较麻烦，需要用到 double。

（多项式的魔盒打开啦！）