joi2023 C

JOI2023 C

【题意】
给定一个 \(n \times m\) 的 \(01\) 网格，有一个 \(k \times k\) 的印章，可以花费 \(1\) 的代价盖在任何一个地方并把这些格子都变成 \(0\)。求使得起点和终点之间有一条只由 \(0\) 组成的边花费的最小代价。

---

考虑正解：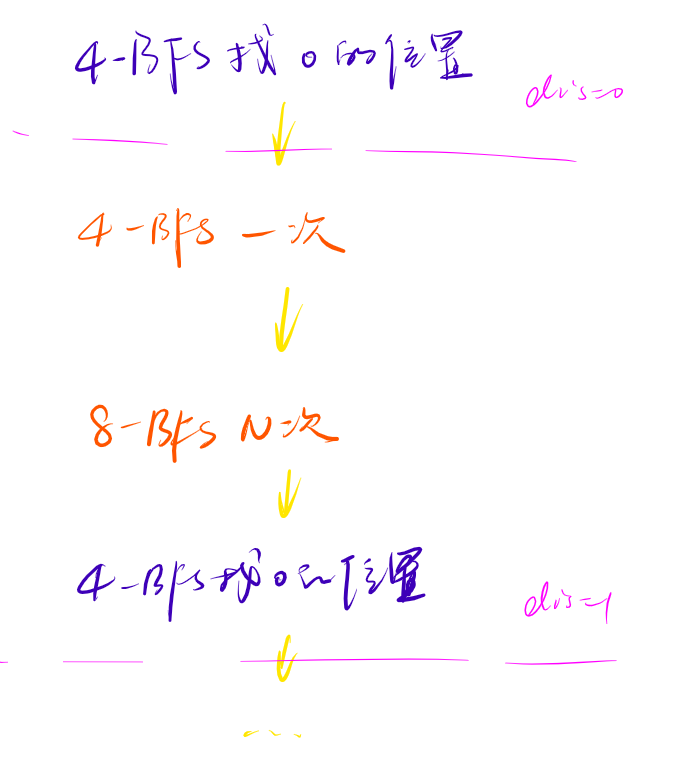

这么一个流程，我们怎么实现能够不退化地完成这个 01-BFS 呢？
先看代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr  << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
    string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; } 
    reverse(s.begin(), s.end()); cerr << s << endl; 
    return;
}
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍！
struct node{int r,c;}s,g;
bool in(int x,int l,int r){return x>=l&&x<=r;}
int r,c,n; bool ok(int x,int y){return in(x,1,r)&&in(y,1,c);}
deque<tuple<int,int,int,int>> q; 
vector<vector<int>> a,d;
int dx[]={0,0,-1,1,-1,1,-1,1};
int dy[]={-1,1,0,0,1,1,-1,-1};
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //freopen();
    //freopen();
    //time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    cin>>r>>c>>n; a.resize(r+10),d.resize(r+10);
    f(i,1,r)a[i].resize(c+10),d[i].resize(c+10);
    cin>>s.r>>s.c>>g.r>>g.c;
    f(i,1,r)
        f(j,1,c){
            char ch;cin>>ch; a[i][j]=(ch=='#'?1:0),d[i][j]=inf;
        }
    q.push_back({0,n,s.r,s.c}); //return 0;
    while(d[g.r][g.c]==inf){
        auto [i,j,k,l] = q.front();
        q.pop_front();
        
        if(d[k][l] != inf) continue;
        d[k][l] = i;//cout <<k<<" "<<l<<" "<<d[k][l]<<endl;
        if(j < n) {
            f(t, 0, 7) {
                if(!ok(k+dx[t],l+dy[t]))continue;
                q.push_back({i,j+1,k+dx[t],l+dy[t]});
            }
        }
        else {
            f(t, 0, 3) {
                if(!ok(k+dx[t],l+dy[t]))continue;
                if(a[k+dx[t]][l+dy[t]]==0){
                    q.push_front({i,j,k+dx[t],l+dy[t]});
                }
                else {
                    q.push_back({i+1,1,k+dx[t],l+dy[t]});
                }
            }
        }
    }
    cout<<d[g.r][g.c]<<endl;
    //time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}
/*
2023/x/xx
start thinking at h:mm


start coding at h:mm
finish debugging at h:mm
*/

（注意，auto [i,j,k,l] = ... 这个东西是 c++17 的，ccf 是不能用的。）

主要就是，考虑记录层数和其距离。

首先，不会出现一个点被遍历两次依然有效的情况。证明和 bfs 的证明是差不多的（前提是第一次的时候以步数为第一关键字，层数为第二关键字是最小的）：考虑该位置可以拓展到什么位置。显然步数相同的时候，层数更小的可以覆盖层数更大的范围。步数不同的时候，可以先走若干步到步数相同的时候，显然更是能覆盖了。因此一个点不会有两次有用。

其次，01bfs 的时候其实也是以步数为第一关键字，层数为第二关键字分层。这就代表了，我们步数增加的时候也要放到队尾。