数据结构优化建图
线段树优化建图
解决的是这样的一类问题:区间对区间连边,在这类图上做一些事情。(先假设是最短路,这个性质好一些)
区间问题会想到线段树。可以想到用线段树建立的虚点做这件事。具体怎么办呢?
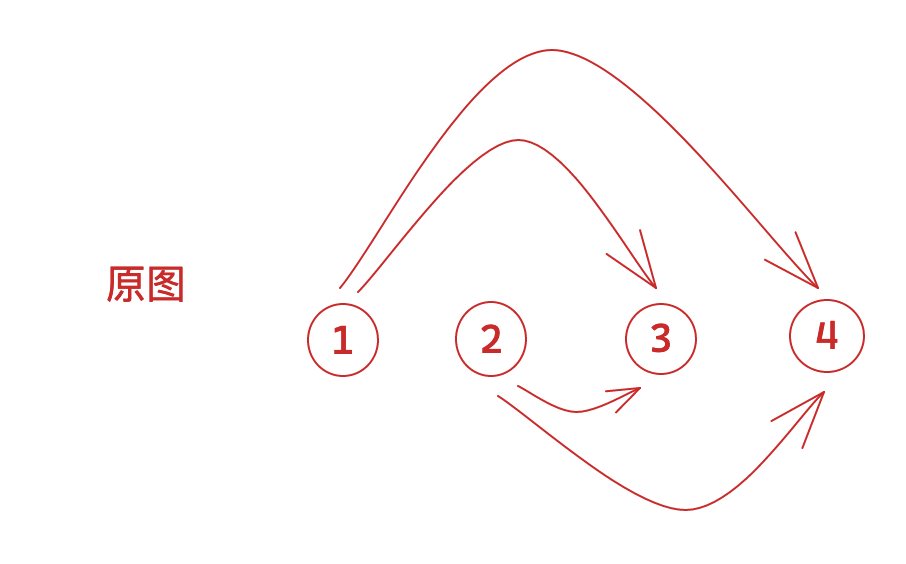
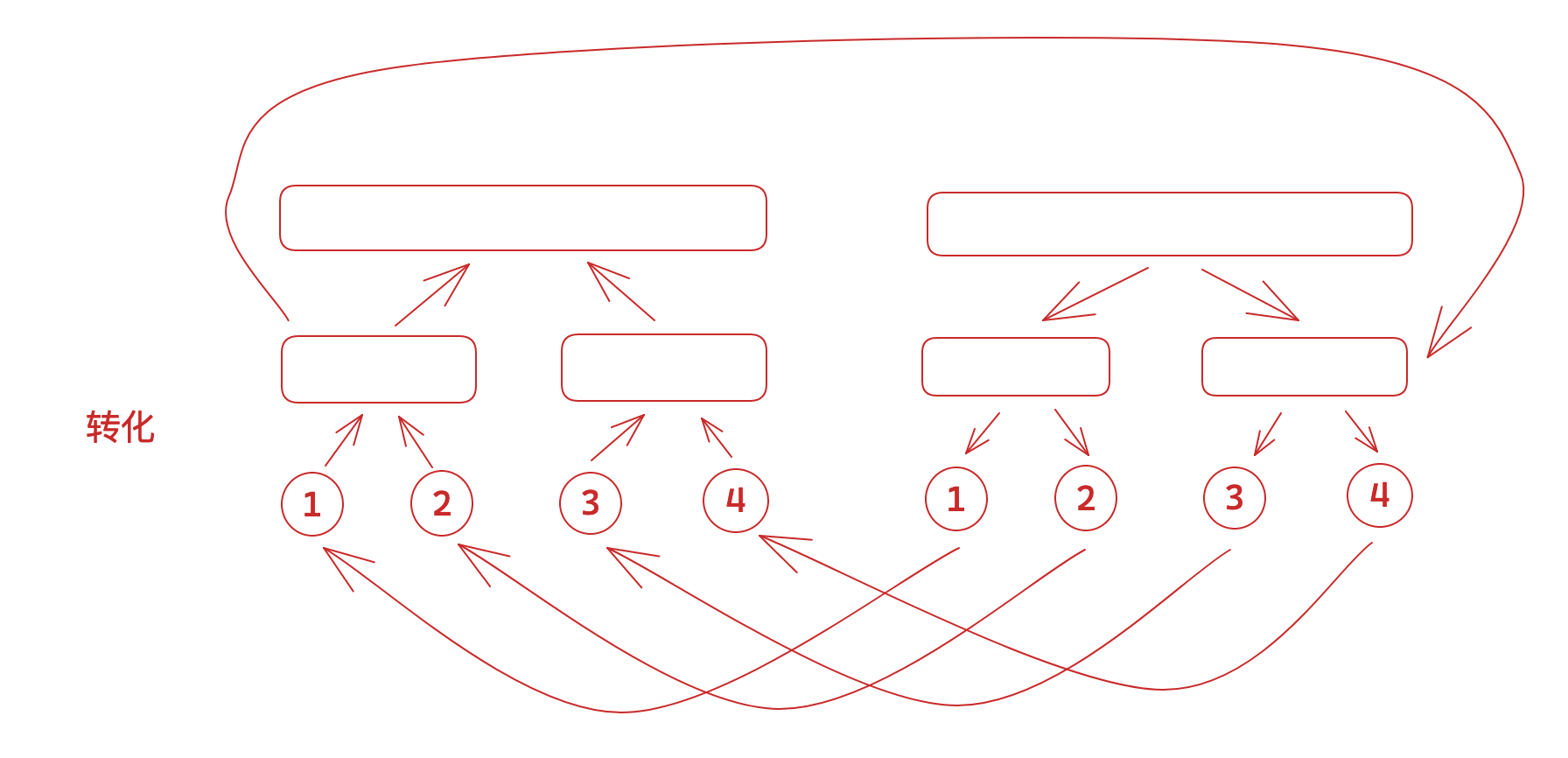
底下两排叶子其实是一样的。也可以缩成一排。看怎么使用。两排的好处也有,点权可以放到上去的边上。
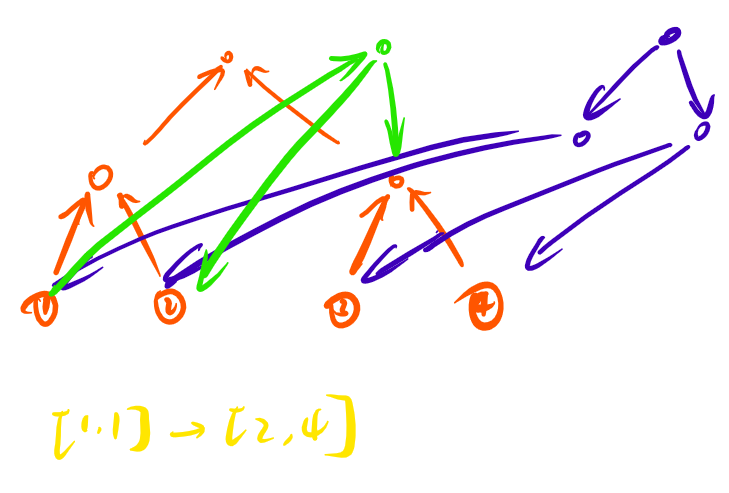
这样做了之后,每一次建边只需要增加一个点和 \(\log\) 条边。
总共 \(4n + T\) 个点,\(T \log n\) 条边。
考虑扩展到二维。
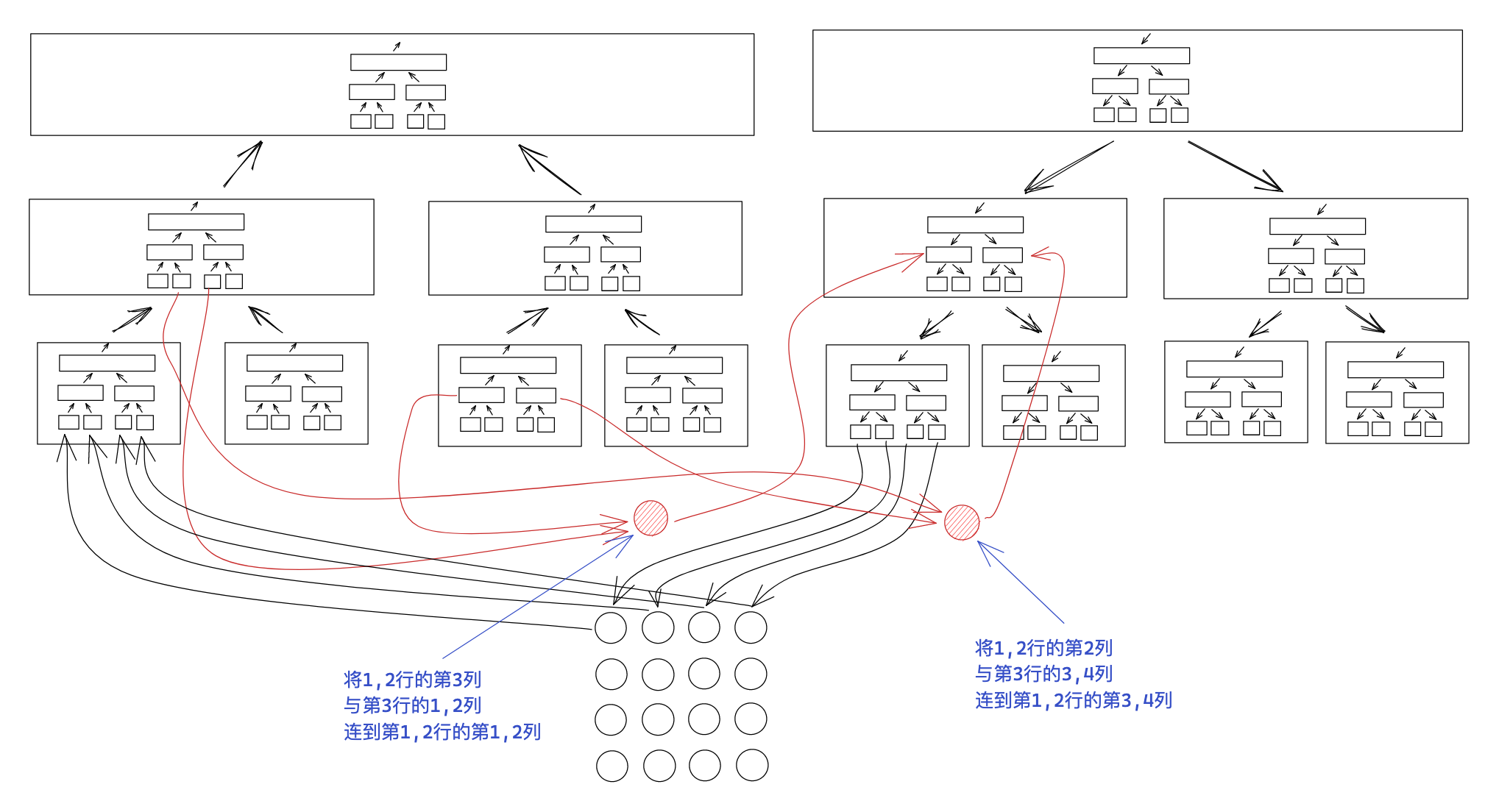
线段树套线段树优化建图。
总共 \(n \log n + T\) 个点,\(T \log n\) 条边。
这样建出来的树其实连通性方面看和原树一样。
模板题:https://codeforces.com/contest/786/problem/B
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e18;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
int cnt;
int root[2];
int lc[1000010], rc[1000010];
vector<pii> g[1000010];
int build(int l, int r, int t) {
if(l == r) {return l;}
int now = ++cnt;
int mid=(l+r)>>1;
lc[now] = build(l, mid, t);
rc[now] = build(mid + 1, r, t);
if(t == 0) {
g[lc[now]].push_back({now,0}); g[rc[now]].push_back({now,0});
}
else {
g[now].push_back({lc[now],0}); g[now].push_back({rc[now],0});
}
return now;
}
void add(int now, int l, int r, int x, int y, int c, int w, int t) {
if(l >= x && r <= y) {
if(t == 0) {g[now].push_back({c,w});}
else {g[c].push_back({now,0});}
return;
}
if(l > y || r < x) return;
int mid=(l+r)>>1;
add(lc[now], l, mid, x, y, c, w, t); add(rc[now], mid + 1, r, x, y, c, w, t);
}
int dis[1000010];
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n, q, s; cin >> n >> q >> s; cnt = n;
root[0] = build(1,n,0); root[1] = build(1,n,1);
// cout << root[0] << " " << root[1] << endl;
f(i, 1, q) {
int op; cin >> op;
if(op == 1) {
int v, u, w; cin >> v >> u >> w;
add(root[0], 1, n, v, v, ++cnt, w, 0);
add(root[1], 1, n, u, u, cnt, w, 1);
}
else if(op == 2) {
int v, l, r, w; cin >> v >> l >> r >> w;
add(root[0], 1, n, v, v, ++cnt, w, 0);
add(root[1], 1, n, l, r, cnt, w, 1);
}
else {
int v, l, r, w; cin >> v >> l >> r >> w;
add(root[0], 1, n, l, r, ++cnt, w, 0);
add(root[1], 1, n, v, v, cnt, w, 1);
}
}
// f(i, 1, cnt) {cout << i << ":" << endl; for(pii j : g[i]) {cout << j.first << " " << j.second << endl;}}
priority_queue<pii> que; f(i, 1, cnt) dis[i] = inf; que.push({0, s});
while(!que.empty()) {
pii nc = que.top(); int now = nc.second, cost = -nc.first; que.pop();
if(dis[now] <= cost) continue;
dis[now] = cost;
for(pii i : g[now]) {
if(dis[i.first] > dis[now] + i.second) {
que.push({-dis[now] - i.second, i.first});
}
}
}
f(i, 1, n) cout << (dis[i] == inf ? -1 : dis[i]) << " ";
cout << endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at 10:05
线段树建实点,两棵,cnt
start coding at
finish debugging at h:mm
*/
前缀优化建图
如果允许弱化版的功能,比如对 \([l,r]\) 以外的点连边,也就相当于前缀后缀连边,那么可以用树状数组的结构简化。
建 \(n\) 个虚点,表示 \(1 \sim n\) 的前缀。建边过程中不需要再建立虚点。只需要连边。
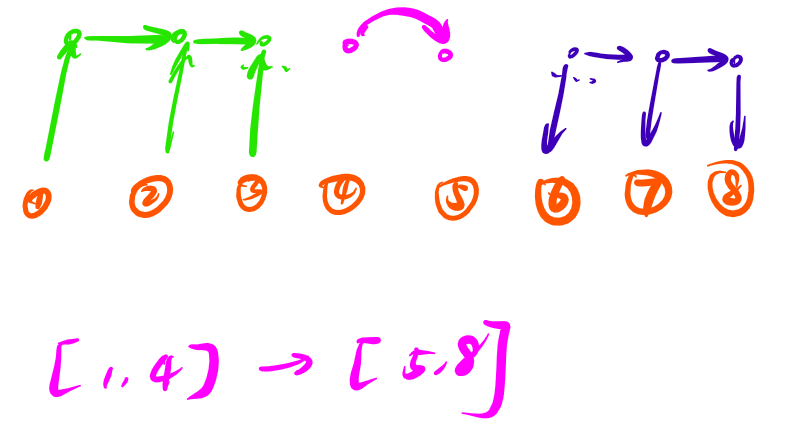
一共 \(2 n\) 个点,\(2n + m\) 条边。
区间拆前后缀优化建图
考虑这样建虚点连边。
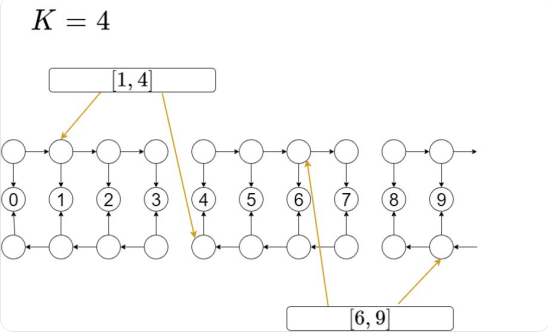
注意到当区间长度固定的时候,可以拆成一个前缀和一个后缀。从而可以优化到 \(O(n)\)。如果区间长度不固定,可能拆成若干个前后缀,是不能这样做的。
应用
最短路:可以求出到区间的最短路。显然是和原图一样的。
拓扑序:可以建立一个包含实点和虚点的拓扑序(实点的拓扑序可以应用)
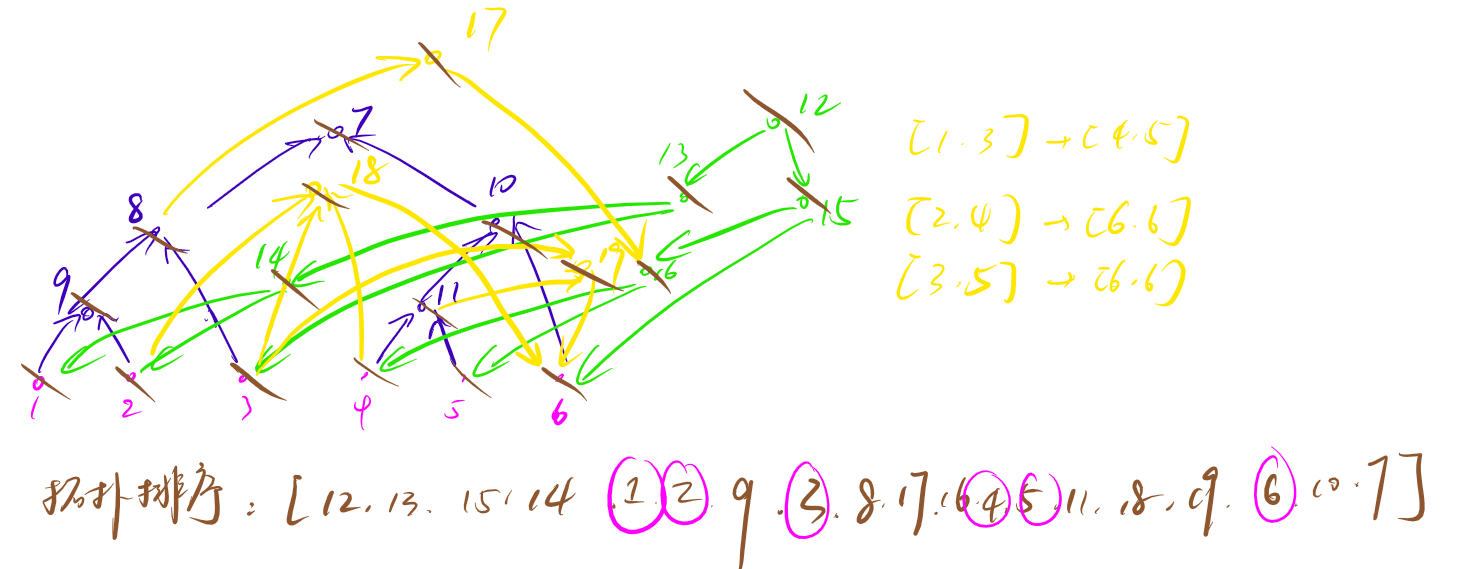
拓扑序的最后一个位置一定是第一棵线段树的根,第一个位置一定是第二棵线段树的根。
如果原图上没有环,那么新图上也不会出现环。
最小生成树:和点有关系,没有那么好搞。
强连通分量:可以在新图上缩点做强连通分量。

