群论初步

在数学和抽象代数中，群论（Group Theory）主要研究叫做「群」的代数结构。

1 群论简介

1.1 定义

在数学中，群（group）是由一种集合以及一个二元运算所组成的，符合「群公理」的代数结构。

一个群是一个集合 $G$ 加上对 $G$ 的二元运算。二元运算用 $\cdot$ 表示，它结合了任意两个元素 $a$ 和 $b$ 形成了一个属于 $G$ 的元素，记为 $a\cdot b$。

群公理包含下述四个性质（有时略去封闭性，只有三个性质）。若集合 $G\neq\varnothing$ 和 $G$ 上的运算 $\cdot$ 构成的代数结构 $(G,\cdot)$ 满足以下性质：

封闭性：对于所有 $G$ 中 $a, b$，运算 $a·b$ 的结果也在 G 中。
结合律（associativity）：对于 $G$ 中所有的 $a, b, c$，等式 $(a \cdot b)\cdot c = a \cdot (b \cdot c)$ 成立。
单位元（identity element，也称幺元）：$G$ 中存在一个元素 $e$，使得对于 $G$ 中的每一个元素 $a$，都有一个 $e \cdot a=a\cdot e=a$ 成立。这样的元素是独一无二的。它被称为群的单位元。
逆元（inverse element）：对于每个 $G$ 中的 $a$，总存在 $G$ 中的一个元素 $b$ 使 $a \cdot b = b \cdot a = e$，此处 $e$ 为单位元，称 $b$ 为 $a$ 的逆元，记为 $a^{-1}$。

则称 $(G,\cdot)$ 为一个群。例如，整数集和整数间的加法 $(\mathbb{Z},+)$ 构成一个群，单位元是 0，一个整数的逆元是它的相反数。

1.2 群的衍生结构

若代数结构 $(G,\cdot)$ 满足封闭性、结合律性质，则称 $(G,\cdot)$ 为一个半群（semigroup）。
若半群 $(G,\cdot)$ 还满足单位元性质，则称 $(G,\cdot)$ 为一个 幺半群（monoid）。
若群 $(G,\cdot)$ 还满足 交换律（commutativity）：对于 $G$ 中所有的 $a,b$，等式 $a\cdot b=b\cdot a$ 成立。则称 $(G,\cdot)$ 为一个 阿贝尔群（Abelian group），又称 交换群（commutative group）。

这些性质对在群上做研究得到的结论有很重要的影响。

1.3 一些特殊的群

整数集合和加法构成群 $(\Z, +)$。
模 $m(m \in \N^*)$ 的整数集合和加法构成群，叫做 $m$ 阶循环群。
所有 $n$ 元置换构成的群，叫做 $n$ 元对称群（Symmetric group）。
所有 $n$ 元偶置换构成的群，叫做 $n$ 元交错群（Alternating group）。
一个正 $n$ 边形的旋转/翻转群有 $2n$ 个元素，被称为 $2n$ 阶二面体群。

1.4 环

环是由一个集合和两个二元运算组成的对象。

形式上，环（ring）是一个集合 $R$ 及对 $R$ 的两个二元运算：加法 $+$ 和乘法 $\cdot$（注意这里不是我们一般所熟知的四则运算加法和乘法）所组成的，且满足如下性质的代数结构 $(R,+,\cdot)$：

$(R,+)$ 构成交换群，其单位元记为 $0$，$R$ 中元素 $a$ 的加法逆元记为 $-a$。
$(R,\cdot)$ 构成半群。
分配律（distributivity）：对于 $R$ 中所有的 $a,b,c$，等式 $a\cdot(b+c)=a\cdot b+a\cdot c$ 和 $(a+b)\cdot c=a\cdot c+b\cdot c$ 成立。

Warning

在有的定义中，环必须存在乘法单位元；相对地，不存在乘法单位元的则被称为伪环（rng 或 pseudo-ring）。遇到的时候需根据上下文加以判断。

维基百科采用的就是这种定义：¹

In the terminology of this article, a ring is defined to have a multiplicative identity, while a structure with the same axiomatic definition but without the requirement for a multiplicative identity is instead called a rng (IPA:/rʊŋ/). For example, the set of even integers with the usual + and ⋅ is a rng, but not a ring. As explained in § History below, many authors apply the term "ring" without requiring a multiplicative identity.

在抽象代数中，研究环的分支为环论。

1.5 环的衍生结构

若环 $R$ 上的乘法还满足交换律，则称 $R$ 为 交换环（commutative ring）。
若环 $R$ 存在乘法单位元 $1$，则称 $R$ 为幺环（ring with identity）。
若幺环 $R$ 的所有非 $0$ 元素 $a$ 存在乘法逆元 $a^{-1}$，则称 $R$ 为除环（division ring）。

1.6 域

域（field）是一个比环性质更强的代数结构，具体地，域是交换除环。

域的研究方法和环大不相同。在抽象代数中，研究域的分支为域论。

2 群的基本性质

群的子群：对于一个群 $(S, \circ)$，一个集合 $S' \in S$ 若和 $\circ$ 也可以构成一个群，那么称群 $(S', \circ)$ 是群 $(S, \circ)$ 的子群。

一个判断有限群的子群的方式：
对于有限群（$S$ 是有限集的群）的一个非空封闭集合，是一个子群。
形式化地说，如果 $S' \in S, S \neq \emptyset, \forall x, y \in S', x \circ y \in S'$，那么 $(S', \circ)$ 是 $(S, \circ)$ 的一个子群。（定义保证群的集合非空）

证明：封闭性由定义得到。单位元存在性：如果不存在单位元，那么对于集合中某元素 $a$，进行任意次 $\circ$ 任意数，均不可以回到 $a$，那么这个子群是无限群。矛盾。（有限群的用处在这里）逆元存在性：考虑 $a^t = e$ 一定存在。

生成子群：对于有限群 $S$ 内的任意一个元素 $a$，定义其在 $S$ 中的生成子群为 $(T, \circ)$，其中 $T = \{a, a \circ a, ..., a \circ a \circ a ... \circ a\}$。$a$ 称为这个子群的生成元。为了方便，记 $a^{(k)} = a \circ ... \circ a$，也就是 $k$ 个 $a$ 进行 $\circ$ 运算的结果。
阶：群 $S$ 中 $a$ 的阶 $ord_S a$ 表示满足 $a^{(k)} = e$ 的最小正整数 $k$。

定理：群 $S$ 中 $a$ 的阶等于其生成子群的规模。

陪集：对于群 $S$ 的一个子群 $T$，考虑 $g \in S$，定义 $g \circ T$ 为 $T$ 在 $S$ 中导出的一个左陪集，同理可以定义右陪集。

容易发现陪集的大小为 $|T|$，陪集可以推出拉格朗日定理，这个定理非常重要。

拉格朗日定理：对于有限群 $G$ 以及其子群 $H$，有 $|G| = |H| \cdot [G:H]$，其中 $[G:H]$ 是 $H$ 在 $G$ 中导出的陪集个数。

证明：首先两个 $H$ 在 $G$ 中导出的陪集一定是无交集或者完全相同的。因为如果 $a \circ h_0 = b \circ h_1$，那么有 $a = b \circ h_1 \circ h_0^{-1} \in bH$（运用了群的封闭性）于是 $aH \subseteq bH$，同理 $bH \subseteq aH$，因此 $aH = bH$。

这个定理的变形：有限群 $G$ 的任何一个子群的大小都被 $|G|$ 整除。

2.1 模运算导出的群

对模 $n$ 运用加法和乘法运算，可以得到两个有限交换群，其中 $n$ 是正整数。
考虑模 $n$ 等价类，$x = [x \% n]_n$。
定义模 $n$ 加法和乘法如下（分别用 $+_n$ 和 $\cdot_n$ 表示）：

\[[a]_n + [b]_n = [a+b]_n [a]_n \cdot_n [b]_n = [ab]_n \]

定义模 $n$ 加法群 $(\Z_n, +_n)$，其规模为 $n$；模 $n$ 乘法群 $(\Z_n^*, \cdot_n)$，$\Z_n^*$ 中元素是和 $n$ 互质的数，其规模为 $\varphi_n$。它们都是有限交换群。

对于某个元素的生成子群，定义阶。其存在周期性，也即 $a^{(1)}, a^{(2)}, ...$ 是周期的。

对其的任意真子群，大小 $\le \cfrac{n}{2}$。这对 miller-rabin 方法的证明有作用。

对任意 $n >1 $ 和任意 $a \in \Z_n^*$，定义 $f_x = ax \mod n$，则其是 $\Z_n^* \rightarrow \Z_n^*$ 的一个映射，是其的一个置换。

3 置换环和染色

定义：

置换：一个一一映射：$\{1,2,...,n\} \rightarrow \{1, 2, ..., n\}$ 或称一个排列。大小为 $n$ 的置换是一个 $n$ 元置换。一般表示为一个上一行为 $1,...,n$，下一行为 $a_1,...,a_n$ 的矩阵。这里简写为 $a_1, ..., a_n$。
置换的循环指标：表示一个置换有多少个置换环。
置换的复合（主要研究的 operation）：对一个置换作用上另一个置换。
置换的逆：为 $rank_1, rank_2, ..., rank_n$。
置换的单位元：为 $1,...,n$。

先来看一些关于置换的性质：

3.1 逆序对交换性质

冒泡排序的时候我们会交换一些相邻的数字，最小交换次数就是逆序对数。这是因为，相邻两个数之外的逆序对数不会改变，只有两个数本身 $(i, j)$ 这一对的一定会发生 $1$ 的变化。没有排好序的时候我们一定能够找到 $i > j$ 进行交换，逆序对 $-1$。

如果我们可以交换任意两个数字，那么排序的最小次数是什么？是置换环个数。考虑对于某一个置换环，我们交换一条环边，可以让 $a_x = y, a_y = z$ 变成 $a_y = y, a_x = z$，增加了一个连通块。最后要 $n$ 个连通块，所以 $n - $ 连通块个数 $=$ 操作次数。

交换任意两个数还有一个性质：考虑逆序对数奇偶性。对于夹在 $i,j$ 中间的数 $k$，考虑 $k, i, j$ 的四种关系，可以推出，交换 $i,j$ 之间的位置不会使得 $ik, jk$ 的逆序对和奇偶性变化；所以所有中间的数不会对奇偶性造成影响。只有 $(i,j)$ 影响了。

因此序列的逆序对个数奇偶性可以看置换环个数，因为任意构造一组交换序列变成 $1 \sim n$ 都可以，准确来说 $n - $ 连通块个数 $=$ 逆序对数。

一个置换的奇偶性定义为其逆序对奇偶性。置换的复合对奇偶性的影响与加法相同：

两个奇置换的复合为偶置换。
两个偶置换的复合为偶置换。
一个偶置换和一个奇置换的复合为一个奇置换。

3.2 置换的 $k$ 次方

考虑一个置换如果做两遍会形成什么。先把置换转换为置换环，然后观察性质。

\[(4235176)^2 = 5231467 \]

\[(4-5-1(-4...))^2 = ((4-1-5(-4...)) \]

\[(7-6(-7...))^2 = (7(-7...)), (6(-6...)) \]

也就是说，置换环变成了从一个点开始每次在原来的环上跳 $2$ 得到的新环，也就是奇数长度的还是 $1$ 个环，偶数长度的破成两个新环，其大小都是 $\cfrac{n}{2}$。

拓展到 $k$ 也是对的。对于每一个数，跳 $k$ 步形成新的置换环。一个长度为 $t$ 的环会变成 $\gcd(k,t)$ 个长度为 $\cfrac{k}{\gcd(k, t)}$ 的环。

3.3 置换群

显然所有 $n$ 元置换组成一个群，称为 $n$ 元对称群。其任意一个子群称为一个置换群。

染色：一个 $n$ 元染色是一个长度为 $n$，元素为数字的数组，表示给每个位置分配一个物品（颜色）的方案。通常用 $c$ 表示染色，$c[i]$ 表示 $c$ 染色给第 $i$ 个位置安排的是什么颜色。
作用：置换作用于染色，意思是将染色按照置换换一下。记作 $p \cdot c$，得到的是一个染色。
染色的结合律：$(p \circ q) \cdot c = p \cdot(q \cdot c)$。
染色的单位性： $e \cdot c = c$

满足这两个性质的群 $G$ 以及染色集合 $C$ 称为广义染色（不需要其他性质，不需要置换环等）

包含集合/群的“乘积”：一般表示集合/群内每个元素的乘积取并集。

3.4 轨道-稳定子群理论

轨道：对于一个置换群 $G$ 和一个染色 $c$，定义 $c$ 在 $G$ 中轨道为 $G \cdot c = \{g \cdot c|g \in G\}$。是一个染色集合。
稳定子群：对于一个置换群 $G$ 和一个染色 $c$，群中满足 $g \cdot c = c$ 的置换构成的是一个群，称为 $c$ 的稳定子群，记为 $G_c$。

为什么是一个群：考虑单位性和逆元存在性显然。并且有结合律，因此 $(f \circ g) \cdot c = c$。有封闭性。

固定：如果染色集合 $X$ 满足 $G \cdot X = X$，那么称 $X$ 在 $G$ 下固定。
轨道-稳定子群定理：对于置换群 $G$ 染色 $c$ 有 $|G \cdot c| \cdot |G_c| = |G|$。

证明：任取 $g \in G$，对于左陪集 $gG_c$ 中的元素 $f = g \times h_0$，有 $f \cdot c = g \cdot c$，因此 $gG_c$ 中每一个元素作用于 $c$ 产生相同元素。另一方面对于不同的两个陪集 $g_1G_c, g_2G_c$，作用于 $c$ 不能产生相同元素，因为如果 $g_1 \cdot c = g_2 \cdot c$ 那么 $c = g_1^{-1} \circ g_2 \cdot c$，那么 $g_1^{-1} \circ g_2 \in G_c \rightarrow g_2 \in g_1G_c$，那么有 $g_2 e = g_1 h_0 e \in g_1 G_c$，与无交矛盾。

因此如果群导出的陪集数量为 $K$，每一个陪集作用于 $c$ 可以得到一个独一无二的染色，因此 $K$ 等于 $c$ 的轨道容量，带入拉格朗日定理得到 $|G| = |G_c| \times |G \cdot c|$。

（简化为一句话：稳定子群导出的一个陪集对应了一个染色方案，于是轨道的容量就是可以导出陪集的个数）

3.5 Burnside 引理和 Polya 定理

是轨道-稳定子群定理的直接推论。

定义两个染色等价：对于置换群 $G$ 和两个染色 $c_1,c_2$，如果存在 $g$ 使得 $gc_1 = c_2$ 那么这两个染色等价。

置换的不动点：对于置换 $g$ 和染色集合 $X$，定义其不动点集合为满足 $g \cdot c = c$ 的 $c$ 的集合。记为 $X^g$。

Burnside 引理：考虑计算对于 $G$ 固定的染色集合 $X$，不等价的染色个数 $K$：

\[K = \cfrac{\sum \limits_{g \in G} X^g}{|G|} \]

其中固定的作用是，令 $G \cdot c$ 一定在 $X$ 中。也就是说和式收集了所有轨道上的染色。

证明：考虑计算 $(g,c) | g \cdot c = c$ 的点对个数。一方面它等于 $\sum \limits_{c \in C} G_c$，一方面它等于 $\sum \limits_{g \in G} X^g$。我们考虑变形第一部分。需要用到轨道-稳定子群定理。

\[\begin{array} \left ~~~~\sum \limits_{c \in C} G_c \\ = \sum \limits_{c \in C} \cfrac{|G|}{|G \cdot c|} \end{array} \]

考虑这个和式，一个轨道上每个数都贡献了 $\cfrac{|G|}{|G \cdot c|}$，那么一个轨道贡献了 $|G|$。（禚级反演）

于是这个和式算出来就是 $|G|K$。除以 $|G|$ 即可得到 $K$。

计算不等价的染色个数是经典问题。并且这个证明只是用到了群的性质，单位性，以及结合性，适合广义染色。

Polya 定理：（就是把不动点个数改写成染色的置换环个数次方）

考虑 $G$ 是置换群，$C$ 是染色群时，burnside 引理的计算方式。

于是这个不动点个数转化为置换环个数。

置换环个数是我们最终要算的东西（虽然还是得找办法算）。

3.6 特殊 $n$ 元置换群的置换环个数和

我们考虑看一些常见的置换群：

完全 $n$ 元置换群
旋转 $n$ 元置换群
旋转/翻转 $n$ 元置换群
二维（以上三种）$n \times m$ 维置换群

计算其 $\sum \limits_{g \in G} X^g$ 的值。

发现这个问题会转化为计数问题：一个群内有多少个置换满足其置换环的个数是 $x$ 个？

完全 $n$ 元置换群

结论：该群内置换环的个数是 $x$ 的排列数就是第一类斯特林数 $\begin{bmatrix}
n \
x
\end{bmatrix} $（$n$ 轮换 $x$）。

我们先明确几个事实：

一个排列可以用若干个置换环表示。
每一个置换环是一个轮换，即顺时针从任意位置开始读都是同一个置换环，而环内元素不能随意交换。
一个置换环唯一确定了置换环内每一个位置的元素，例如 $(4 6 2 3)$ 代表了 $a_4 =6, a_6=2,a_2=3,a_3=4$。（如果环内元素进行交换/翻转则不同，例如 $(3246)$ 代表了 $a_3 = 2$ 而不是 $a_2=3$。
一个排列分成的若干个置换环没有顺序。

对轮换这个数学对象进行计数的就是第一类斯特林数。原问题其实是需要对 $n$ 个数排成 $x$ 个无序轮换计数，这恰好对应了第一类斯特林数的定义。

所以 $\sum \limits_{g \in G} X^g$ 其实强于第一类斯特林数的行求和。这个离了多项式不能做，所以直接暴力做是最好的了。

旋转 $n$ 元置换群（P4980）

多测，给定一个 $n$ 个点，$n$ 条边的环，有 $n$ 种颜色，给每个顶点染色，问有多少种本质不同的染色方案，答案对 $10^9+7$ 取模。

群是 $(1,2,3,...,n)$ 经过若干次顺时针旋转一格操作得到的群，可以发现做 $i$ 次旋转得到的置换的置换环个数是 $\mathrm{gcd}(i, n)$。这可以由是 $(1234...n)$ 这个置换环的 $i$ 次方直接得出。

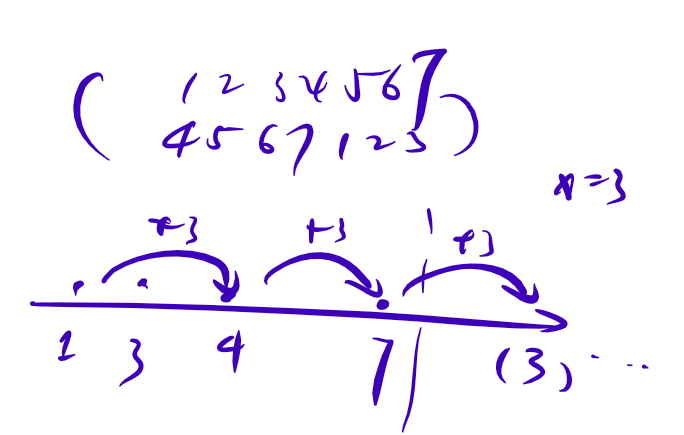
因此要求的是 $\sum \limits_{i = 1} ^ n n^{\gcd(i, n)}$。

考虑 $\gcd(i, n) = d$ 的方案数即为 $\varphi_\frac{n}{d}$。

因此可以预处理 $\varphi$，同样用 $O(n)$ 时间得到答案。

旋转/翻转 $n$ 元置换群

翻转，意思是可以将整个置换进行翻转，或者说，可以逆时针旋转。但是顺逆时针并没有什么比较好的关联，所以我们分类。

没有旋转的是上面这一部分，有旋转的你会发现其实很简单。

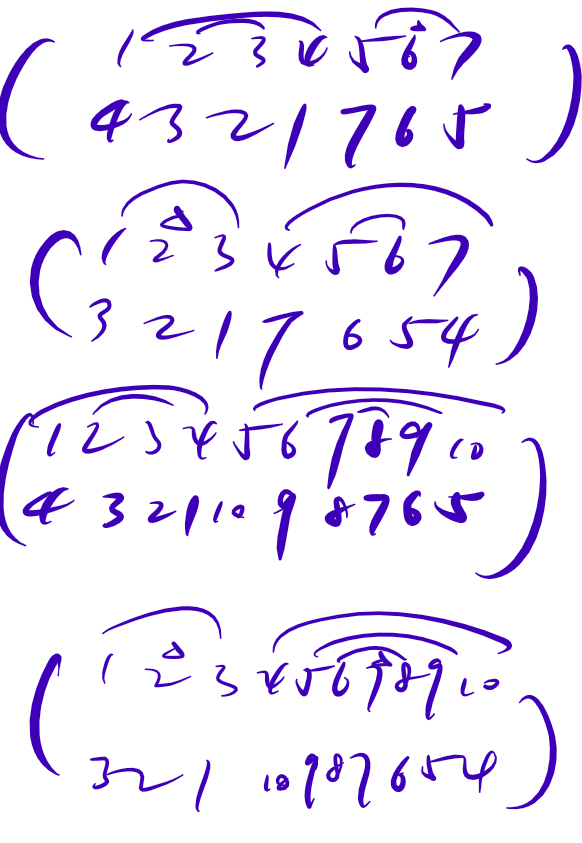
对于奇数：$n$ 种长度为 $\lfloor\cfrac{n+1}{2} \rfloor$ 的。

对于偶数：$\cfrac{n}{2}$ 种长度为 $\lfloor\cfrac{n}{2} \rfloor$ 的以及$\cfrac{n}{2}$ 种长度为 $\lfloor\cfrac{n}{2} \rfloor + 1$ 的。

二维置换群

给定一个矩阵染色，先对 $x$ 轴作用上一个置换，然后对 $y$ 轴作用上一个置换。

考虑每个环之间是独立的，因此对于两个维度上一对长度为 $(a, b)$ 的环，其生成的一个环的长度为 $\mathrm{lcm}(a,b)$（证明好做，就是考虑每次跳，什么时候回到原点），于是可以生成 $\gcd(a,b)$ 个环。因此对于两个维度上分别可以表示成若干个长度为 $(a_1,a_2,...,a_x),(b_1,b_2,...,b_y)$ 的置换环两对置换，其环个数为 $\sum \limits_{i, j} \gcd(a_i, b_j)$。

对于两个完全 $n$ 元置换群的复合，利用一维的结论就不好做了，因为完全没有对长度的研究。但是你注意到式子对每一个长度是独立的，所以你只要计算所有排列中长度为 $x$ 的环出现的次数，就可以计算这个式子。而这个次数也是一个组合数乘以第一类斯特林数的形式罢了。

对于旋转置换群和翻转置换群，由于长度最多两种，所以很好办的。反正遇到了推推就好了。

4 生成子群结构

生成子群结构是一个高效的维护一个生成集的生成子群或者其所有子集的生成子群，并支持在生成集中加入元素的结构。

考虑一个群 $|G|$，对于其的一个子集 $|H|$，其生成子群定义为仅用 $|H|$ 内元素进行 operation 即可生成的所有元素所构成的子群，不妨记为 $G_H$。

设想如果将子群 $H$ 扩充一个元素 $x$，那么其生成子群会有什么变化呢？

你可能会想到 $x$ 的生成子群 $G_x$ 和 $G_H$ 进行一些什么样的操作使得其能够变成一个更大的生成子群，例如，对 $G_x$ 和 $G_H$ 中的每一对元素做 operation 形成一个新的集合？很遗憾，这样并不是正确的：

我们不妨考虑 $H$ 中某一个元素 $y$ 和 $x$ 做 operation 的结果，例如 $y\circ y\circ x\circ y \circ x$。假设先前的结果成立，那么 $G_H$ 中可能有 $y, y \circ y, y \circ y \circ y, ...$，$G_x$ 中可能有 $x \circ x \circ ... \circ x$。那么对它们进行一次 operation 可能得到 $\epsilon, y, y \circ y, ..., x, y \circ x, y \circ y \circ x, x \circ x, y \circ x \circ x, ...$。但是 $y \circ y \circ x \circ y \circ x$ 并不会被获得！你也许会说，它生成了 $y \circ y \circ y \circ x \circ x$。但是由于没有交换律，这两个并不相等。于是这个方式就错了。（如果有交换律，那么这个方式是对的）

这里介绍一个比这样暴力操作时间复杂度更好，并且能做没有交换律的情况的一个结构：生成子群结构。一个子群在该结构里被描述为一张有所有元素的图，其中有一些连边，这些连边将整张图划分为了若干个连通块。特别地，一条直接连边表示其中一个端点可以由另一个 operation 上生成集内的某一个元素直接到达。那么一个连通块代表了一个子群/子群的陪集，所有子群/陪集大小相等，因此一个子群的大小就是集合大小除以子群个数。其中含有幺元的一个连通块是这个子群，其他连通块都是陪集。

这个结构显然可以方便地维护每一个子群以及其大小。但是最重要的是它能够直接合并向生成集中加入元素的过程。加入元素的时候，直接从全集 $G$ 中的每一个元素和其 op 上该元素得到的节点连边。例如上述的结构就可以证明得到了任何 $x$ 和 $y$ 的组合：假设存在一个元素它由 $xyx^3y^4x$ 组成，那么在加入 $y$ 之前，有 $\epsilon \rightarrow x, xy \rightarrow xyx, xyx^3y^4 \rightarrow xyx^3y^4x...$ ，加入 $y$ 的时候将所有需要使用 $y$ 组成的东西连接上了，这样就可以保证一定得到了所有包含 $x$ 和 $y$ 的组合。

这样一次合并的时间复杂度为 $O(|G|)$，并且由于拉格朗日定理，每一次合并必然使得其中一个子群大小乘以 $2$（并不是较小的那个子群大小乘以 $2$，而是任意子群大小必然都乘以 $2$，这是由于合并一个陪集，陪集的大小就等于子群的大小）所以任何一个子群必然最多被合并 $O(\log |G|)$ 次。这意味着如果从生成集中没有元素一直扩充，并且实时维护子群大小，那么时间复杂度是 $O(|G| \log^2 |G|)$ 的，如果按秩合并那么可以减少一个 $\log$ 因子。

要点：判断加入一个元素后某一个子群是否扩张，就只需要考虑这个元素是否在子群内部即可，相当于询问这个元素和幺元是否位于同一个集合内部，这可以 $O(\log |G|)$ 判断，如果你不按秩合并而是编号比较小的做父亲，那么可以 $O(1)$ 判断。

【要点总结】

一个子群对应一张图。
判断是否需要扩张就是判断是否在群内。

求一个群的本质不同子群个数

考虑扫描线扫描每个元素，维护第一个元素到这个元素的这段区间内，选择其中一些元素成为生成集，形成的所有子群。容易发现增加一个元素的时候可以将每一个子群拉出来判断是否可以扩张，如果可以扩张那么就扩张出去。

发现这样做会扩张到相同的位置，我们使用异或哈希可以方便地求出是否有与之相同的子群，但是笔者目前还不知道没有求出整个群的条件下如何发现会扩张到已有的元素。

如果不会扩张到已有元素，那么时间复杂度为 $O(n|G| \log ^2 |G|)$，其中 $n$ 是不同子群的个数。但是这个限制比较松，所以加上可能扩张到已有元素的也能跑。

例如，求 $k$ 阶对称群的本质不同子群个数，可以这样求：

vector<int> p[140]; map<vector<int>, int> pid; int sum; int val[140]; map<int, int> s; 
int mul(int x, int y) {
    vector<int> th = p[x], op = p[y]; vector<int> res = th; f(i, 0, (int)th.size() - 1) res[i] = op[th[i]]; 
    return pid[res]; 
}
struct subgroup {
    int fa[140], cnt, hx[140];
    subgroup() {cnt = sum; f(i, 0, sum - 1) fa[i] = i, hx[i] = val[i]; }
    int getfa(int x) {if(fa[x] == x) return x; else return fa[x] = getfa(fa[x]); }
    void merge(int x, int y) {
        x = getfa(x), y = getfa(y); if(x != y) {if(x < y) swap(x, y); cnt--, fa[x] = y; hx[y] ^= hx[x]; }
    }
    bool isin(int x) {x = getfa(x);int y = getfa(0); return x == y; } //0 是幺元
}sg[250];
signed main() {
int k; cin >> k; vector<int> v; f(i, 0, k - 1) v.push_back(i); 
    do {pid[v] = sum; p[sum ++] = v; } while(next_permutation(v.begin(), v.end())); 
    f(i, 0, sum - 1) val[i] = rng(); 
    int amt = 1; sg[1] = subgroup(); s[sg[1].hx[0]] = amt; 
    f(i, 0, sum - 1) {
        int tmp = amt;
        f(j, 1, tmp) {
            if(!sg[j].isin(i)) {
                subgroup newsg = sg[j]; f(t, 0, sum - 1) newsg.merge(t, mul(t, i));
                if(!s.count(newsg.hx[0])) {s[newsg.hx[0]] = ++amt; sg[amt] = newsg; }
            }
        }
    }
cout << amt << endl; 
}

$k=5$ 的时候得到 $156$，所以遇到 $k \le 5$ 的对称群 hard 问题可以往这上面想（？

CF1229D. Wojtek and Card Tricks

给定一组长度为 $k$ 的排列 $p_1, ..., p_n$，求 $\sum \limits_{1 \le l \le r \le n} f(l,r)$，其中 $f(l,r)$ 是 $a_l, a_{l+1}, ..., a_r$ 构成集合的生成子群个数。

$n \le 200000, k \le 5$

扫描线扫右端点，维护每一个左端点的生成子群。扩张的时候我们可以二分出一个 $l$ 使得 $l \sim i$ 处的答案需要更新。判断是否需要更新的过程上面说过了可以看 $a_i$ 是否在子群里。

这样做的时间复杂度是 $O(n \log n \log k! + n \log k! k!)$，还不能通过，但是我们可以用上述求一个群的本质不同子群的方法，预处理所有子群以及它扩张上一个元素的结果。这样时间复杂度变为 $O(n \log n \log k! + n \log k! +amt \times k \log k!)$，可以通过，其中 $amt = 156$。

vector<int> p[140]; map<vector<int>, int> pid; int sum; int val[140]; map<int, int> s; 
int mul(int x, int y) {
    vector<int> th = p[x], op = p[y]; vector<int> res = th; f(i, 0, (int)th.size() - 1) res[i] = op[th[i]]; 
    return pid[res]; 
}
struct subgroup {
    int fa[140], cnt, hx[140];
    subgroup() {cnt = sum; f(i, 0, sum - 1) fa[i] = i, hx[i] = val[i]; }
    int getfa(int x) {if(fa[x] == x) return x; else return fa[x] = getfa(fa[x]); }
    void merge(int x, int y) {
        x = getfa(x), y = getfa(y); if(x != y) {if(x < y) swap(x, y); cnt--, fa[x] = y; hx[y] ^= hx[x]; }
    }
    bool isin(int x) {x = getfa(x);int y = getfa(0); return x == y; } //0 是幺元
}sg[250];
int tran[250][140]; int cur[200010]; 
signed main() {
    int n, k; cin >> n >> k; vector<int> v; f(i, 0, k - 1) v.push_back(i); 
    do {pid[v] = sum; p[sum ++] = v; } while(next_permutation(v.begin(), v.end())); 
    f(i, 0, sum - 1) val[i] = rng(); 
    int amt = 1; sg[1] = subgroup(); s[sg[1].hx[0]] = amt; 
    f(i, 0, sum - 1) {
        int tmp = amt;
        f(j, 1, tmp) {
            if(!sg[j].isin(i)) {
                subgroup newsg = sg[j]; f(t, 0, sum - 1) newsg.merge(t, mul(t, i));
                if(!s.count(newsg.hx[0])) {s[newsg.hx[0]] = ++amt; sg[amt] = newsg; }
            }
        }
    }
    f(i, 1, amt) {
        f(j, 0, sum - 1) {
            if(sg[i].isin(j)) tran[i][j] = i; 
            else {
                subgroup newsg = sg[i]; f(t, 0, sum - 1) newsg.merge(t, mul(t, j));
                tran[i][j] = s[newsg.hx[0]]; 
            }
        }
    }
    int ians = 0, ans = 0; 
    f(i, 0, n - 1) {
        vector<int> ai; ai.resize(k); f(j, 0, k - 1) {cin >> ai[j]; ai[j]--; } int tid = pid[ai]; 
        int l = 0, r = i - 1;
        while(l < r) {
            int mid = (l + r) >> 1; 
            if(!sg[cur[mid]].isin(tid)) r = mid;
            else l = mid + 1; 
        }
        f(j, l, i - 1) {
            ians += sum / sg[tran[cur[j]][tid]].cnt - sum / sg[cur[j]].cnt; 
            cur[j] = tran[cur[j]][tid];
        }
        cur[i] = tran[1][tid];
        ians += sum / sg[cur[i]].cnt;
        ans += ians; 
    }
    cout << ans << endl; 
}

posted @ 2023-02-18 21:28 OIer某罗阅读(291) 评论(0) 编辑收藏举报

刷新页面返回顶部

Zeardoe