数论卷积相关
积性函数
如果函数是积性函数,那么只需要知道其在 处的取值,那么已经完全了解了这个函数。这极大简化了问题。
随便看个例子:求因子和函数 是什么。
首先证明是积性函数。考虑 ,因此是积性函数。
其次考虑其在 处取值: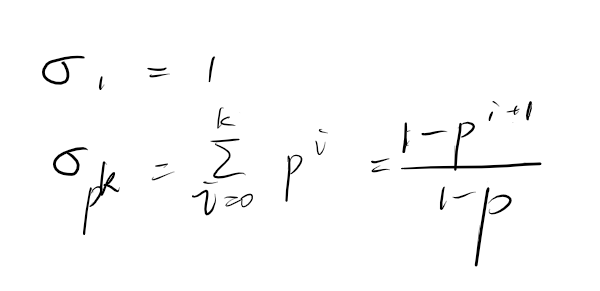
因此可以乘起来就知道了。
接下来再看看欧拉函数是什么。怎么证明积性函数:
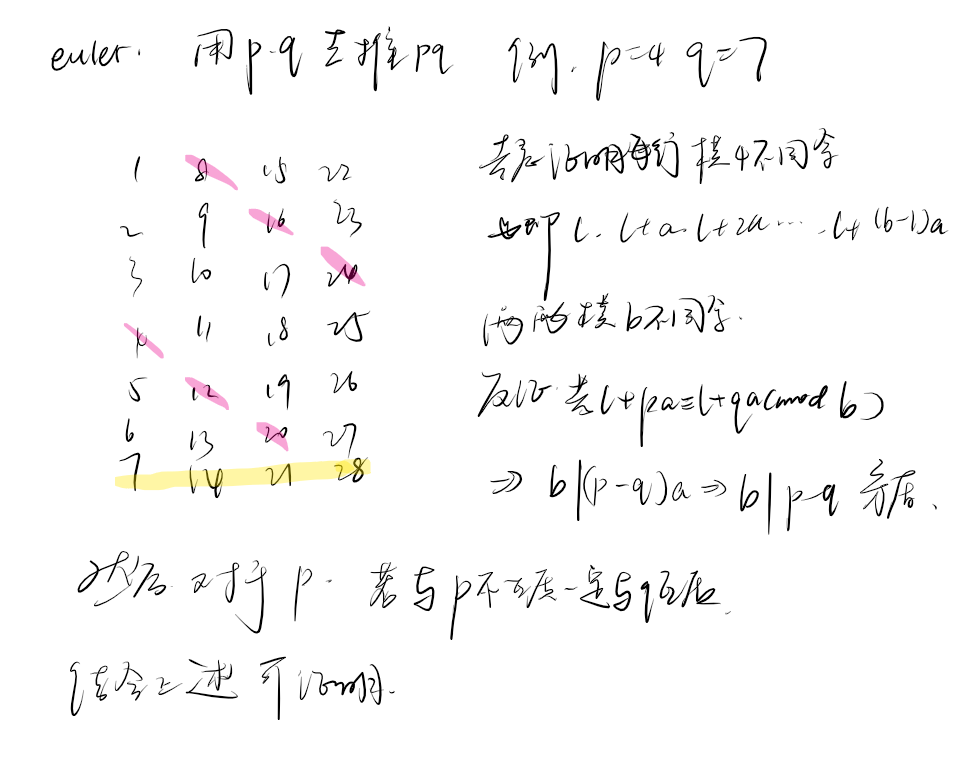
那是什么就乱证。
逆元,单位元的定义
单位元 ,也叫做幺元。其在一个半群 (前一个是元素集合,后一个是运算符)中被定义的话,半群被称作幺半群。
某一个元素 的逆元 ,意思是 。
例如,
对于 ,,因此 。
对于 ,,因此 。
对于 (矩阵乘法), 单位矩阵(主对角线是 其他都是 )。
Dirichlet 卷积
也叫乘法卷积。
对于两个数列 ,定义 为 做狄利克雷卷积的结果。也称 。那么 。朴素地进行一次狄利克雷卷积,时间复杂度为 。
性质:
对于两个积性函数 , 是积性函数。容易证明。(有什么用?积性函数有一些牛逼的筛法和性质)
在此基础上,定义一些特殊函数。
函数:,是完全积性函数。
函数:半群 的单位元。考虑其性质:
当 时,,显然 。
当 时,,显然 。
因此 。
函数:也叫做莫比乌斯函数。是 函数的逆元。也即,
当 时,,显然 。
当 时,,显然 。
为了简便,我们发现可以省去 。接着看看。
当 时,,那么当 的时候 。
当 时,,那么 。
二项式反演得,。
当 时,需要 。
验证一下,确实能对的上。
因此
有一个东西是要注意到的。 等于 。
莫比乌斯反演
,第二个过程就是莫比乌斯反演。
有什么作用?对于某一项的性质可以追踪。例如 ,可以判断 。
莫比乌斯函数是积性函数,可以通过线性筛求。其中素数赋 ,最小质因子乘上的时候赋 ,否则赋相反数。
POI2007 Zap(BZOJ1101)
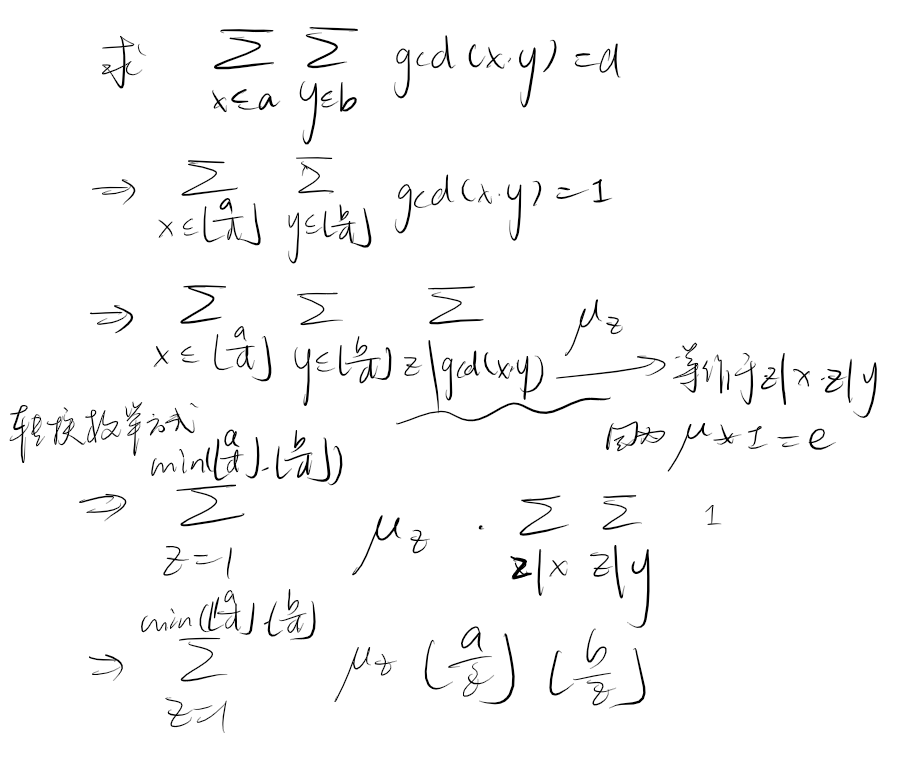
整除分块即可。这是非常经典的应用。虽然在 的时候具有 的简便方法,但是这个推法显然是更为能够推广的。
拓展式子
,其中 。
证明:
首先这三个都是积性函数,因此只需证明对任意 都成立,那么对所有正整数均成立。
考虑 。
因此
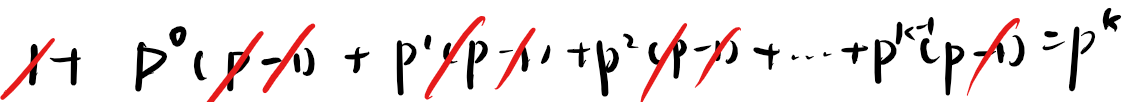
得证。
狄利克雷前缀和
更优秀的求 的方式。用 进赋值序列的视角看待,是一个高维前缀和。注意 没啥特别的,没有 这一维度。
时间复杂度 ,比一般的 要好。
P5495
f(i, 1, cnt) for(int j = p[i]; j <= n; j += p[i]) a[j] += a[j / p[i]];
类似地,可以卷 ,也就是前缀和的逆运算。还不用筛。
f(i, 1, cnt) for(int j = n / p[i]; j >= 1; j --) a[j * p[i]] -= a[j];
P2714
gcd 卷积。
这个算超集和,就是 FMT。不需要显式的 进赋值序列,只需要直接枚举 即可。
注意卷积里面 分别是多少。
最后容斥做的时候一定要推清楚。系数是一个组合数行求和形式。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
const int v = 10000;
int p[10010]; bool c[10010]; int cnt; int a[10010], b[5][10010];
void euler() {
f(i, 2, v) {
if(!c[i]) {p[++cnt] = i;}
for(int j = 1; j <= cnt && p[j] * i <= v; j ++) {
c[p[j] * i] = 1;
if(i % p[j] == 0) break;
}
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
euler();
int n;
while(cin >> n) {
memset(a, 0, sizeof(a)); memset(b, 0, sizeof(b));
f(i, 1, n) {cin >> a[i]; b[1][a[i]] ++;}
//对 b 做 gcd 卷积
f(i, 1, v) b[0][i] = b[1][i];
f(j, 1, cnt) { //维度
for(int k = v / p[j]; k >= 1; k --) {
b[0][k] = b[0][k * p[j]] + b[0][k];
}
}
f(i, 1, 3) {
//FWT
f(j, 1, v) b[i + 1][j] = b[i][j];
f(j, 1, cnt) { //维度
for(int k = v / p[j]; k >= 1; k --) {
b[i + 1][k] = b[i + 1][k * p[j]] + b[i + 1][k];
}
}
//点值乘法
f(k, 1, v) b[i + 1][k] *= b[0][k];
//IFWT
f(j, 1, cnt) {
for(int k = 1; k <= v / p[j]; k ++) b[i + 1][k] = b[i + 1][k] - b[i + 1][k * p[j]];
}
}
b[2][1] -= b[1][1]; b[2][1] /= 2;
b[3][1] -= b[1][1]; b[3][1] -= 6 * b[2][1]; b[3][1] /= 6;
b[4][1] -= b[1][1]; b[4][1] -= 14 * b[2][1]; b[4][1] -= 36 * b[3][1]; b[4][1] /= 24;
cout << b[4][1] << endl;
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at h:mm
finish debugging at h:mm
*/
狄利克雷除法
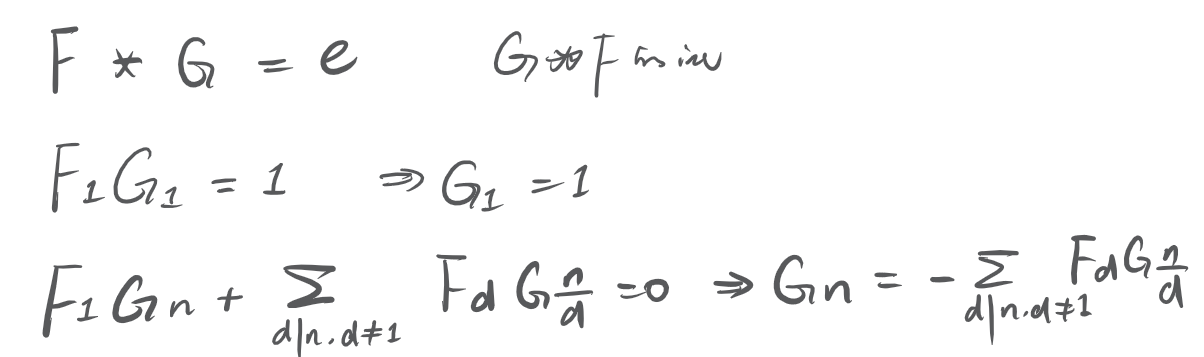
递推,先解出 ,时间复杂度 ,然后卷。
总时间 。
性质
狄利克雷卷积有交换律和结合律。(这个乱证)
两个积性函数做狄利克雷除法的结果是积性函数。
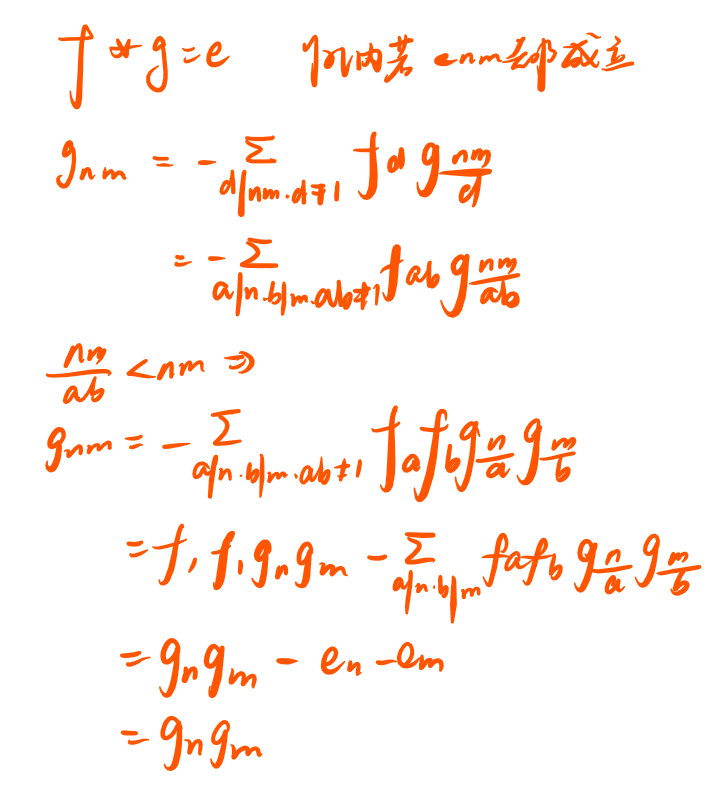
powerful number 筛
powerful number,是没有非平方因子的数。 的 powerful number 的规模是 的。
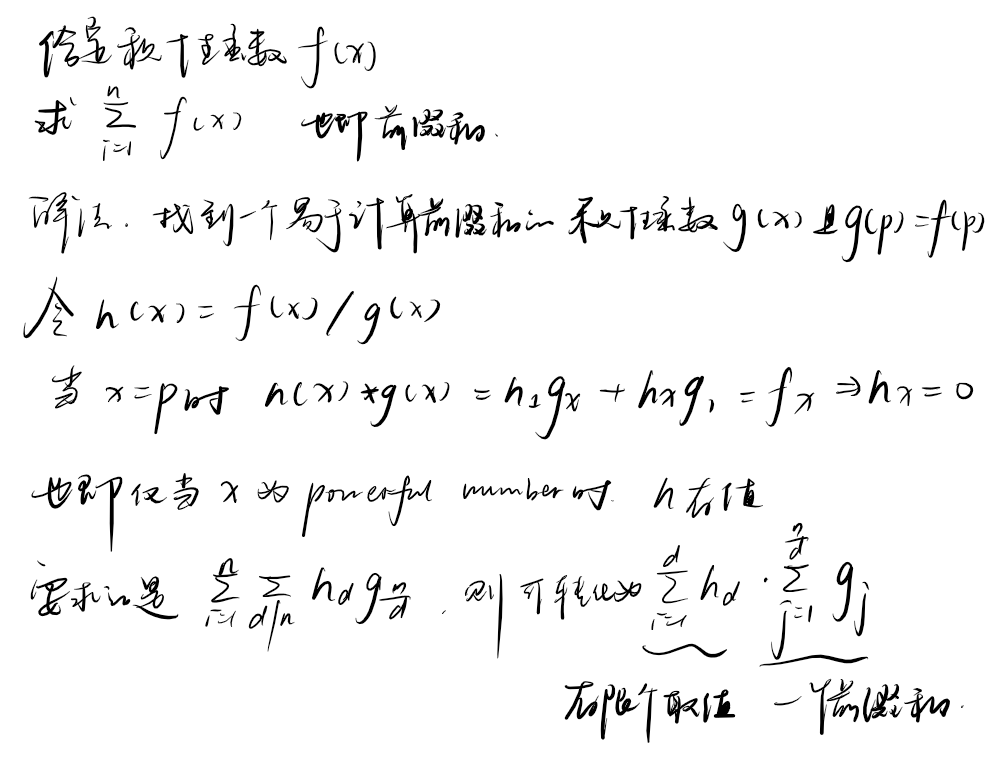
时间复杂度 , 是查询一次 前缀和的时间。
2.2 模拟赛 T2 数论导数
【题意】

【分析】

怎么求 在 的时候的取值?首先 是积性函数。因此只需要知道 和 的取值就可以乘出所有取值。注意 对所有 都成立。
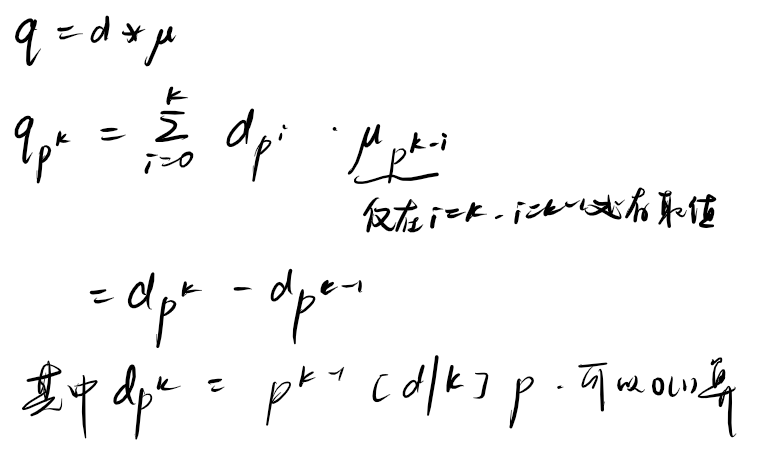
积性函数的性质非常神奇,一定要懂得用。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· 什么是nginx的强缓存和协商缓存
· 一文读懂知识蒸馏
· Manus爆火,是硬核还是营销?