NP 理论
算法导论，第 34 章。
P：Polynomial Problem，指的是确定可以在多项式时间内解出的问题。
NP：Non-Deterministic Polynomial Problem，非确定性多项式问题。指的是其解的正确性可以再多项式时间内被检查的问题。（能被检查说明什么呢？我们可以找到所有可能解的集合然后验证它们。）
NP-Complete：一类特殊的 NP 问题，特殊之处在于所有 NP 问题都可以多项式归约到 NP-Complete 问题上。
NP-Hard 问题，所有 NP 问题都可以多项式归约到 NP-Complete 问题上。但是不一定是 NP 问题。
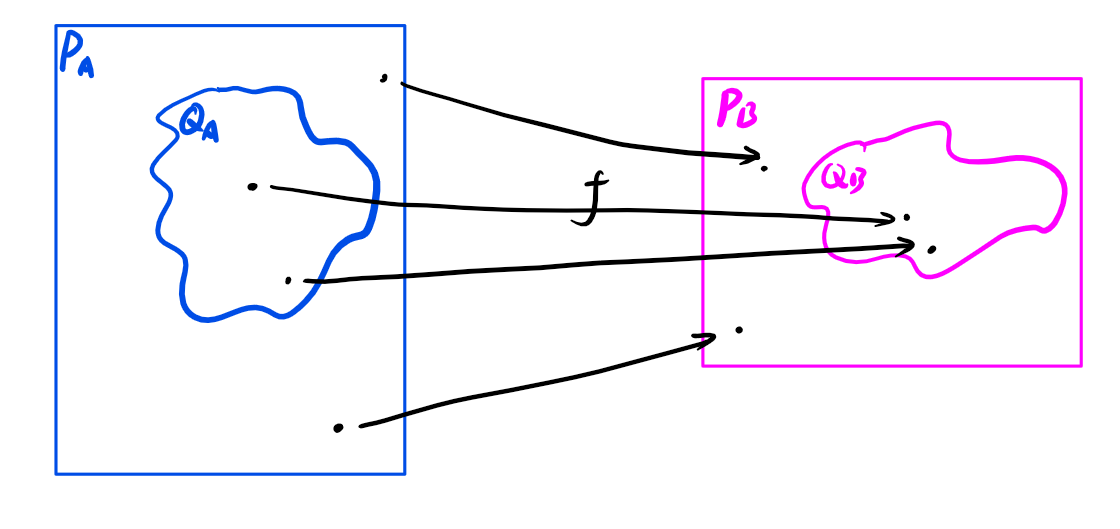
什么是归约（Reduction）：对于问题（看成函数）\(A\) 和问题 \(B\)，考虑它们可能解的集合 \(P_A\) 和 \(P_B\) 和它们解的集合 \(Q_A\) 和 \(Q_B\)（显然 \(Q_A \subseteq P_A\) 且 \(Q_B \subseteq P_B\)）。如果存在一个多项式时间算法映射 \(f: P_A \rightarrow P_B\) 使得可能解 \(i \in Q_A\) 当且仅当 \(f(i) \in Q_B\)（也就是说，如果存在 \(x \in Q_A\)，则 \(f(x) \in Q_B\)；如果存在 \(x \in \complement_{P_A}Q_A\)，则 \(f(x) \not \in Q_B\)），那么如果求出了 \(Q_A\) ，那么可以求出 \(Q_B\)；如果知道是否存在 \(f(x) \in Q_B\)，那么知道是否存在 \(x \in Q_A\)。（对于 \(Q_A\) 内每个解映射一次即可）也就是说，如果能解决问题 A，那么一定能解决问题 B。那么也就称 问题 B 可以归约为问题 A。（A 的解稍作处理可以变成 B 的解，解 B 的一个方法是先解 A；想解决问题 B，可以交给问题 A 来处理）
如果 A 解出来了就可以解出来 B 了（B 可以归约为 A），但是 B 是 NP 问题，那么 A 肯定也是 NP 问题。
如何证明 NP-Complete
有两个方法：
- 找到一个 NP-Complete 问题，归约到这个问题。也就是你的解法可以解决这个 NP-Complete 问题。
- 所有的 NP 问题都可以归约到你的问题。
显然在第一个 NP-Complete 问题被找到之前，不能用第一种方法。而这个问题就是 Circuit-SAT Problem。这个问题被证明是 NP-Complete 的。
Circuit-SAT Problem：一个包含 Xor, Or, And 等的门电路，输入一些 \(0/1\) 使得输出为 \(1\) 是否有解。
从它开始推出来（被归约）了很多 NP-Complete 问题，知道即可，不需要会证明：
-
SAT 问题：\(n\) 个布尔变量，\(m\) 个布尔连接词：具有一个/两个输入，一个输出的任何布尔函数，例如：ans, or, \(\rightarrow\), \(\leftrightarrow\)，一些括号组成的表达式 \(\phi\) 是否可能为真。
-
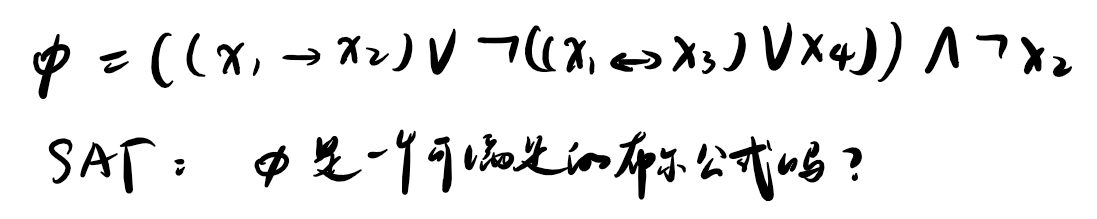
3-CNF-SAT 问题：\(n\) 个布尔变量，\(m\) 个语句，每个语句恰好三个变量 or 构成，语句之间用 and 连接。问其是否能够为真。
-
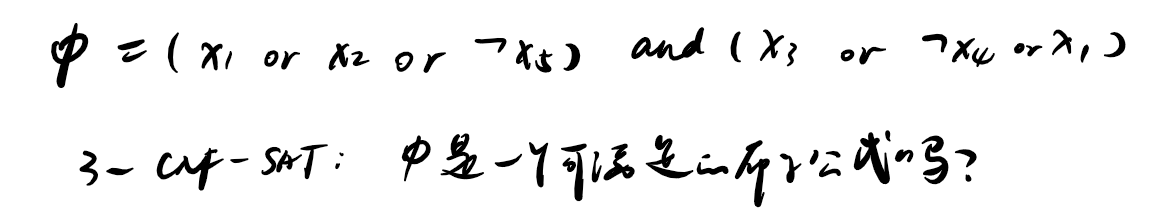
团问题：简单无向图 \(G = (V, E)\) 中的团是点集 \(V' \in V\)，满足其中每对点之间都有边连接。求是否存在大小为 \(k\) 的团。（或者，最大团大小是什么）
-
顶点覆盖问题：简单无向图 \(G = (V, E)\) 中的顶点覆盖是点集 \(V' \in V\)，满足 \(E\) 中的每条边，其中至少一端在 \(V'\) 中。求是否存在大小为 \(k\) 的顶点覆盖。
-
子集和问题：给定正整数有限集合 \(S\) 和一个整数目标 \(t > 0\)，问是否存在一个子集 \(S' \in S\)，使得其元素和为 \(t\)。
-
哈密顿回路问题：无向图存在哈密顿回路吗？
-
旅行商问题：\(n\) 点 \(m\) 边无向图，边有边权，求最小权哈密顿回路。
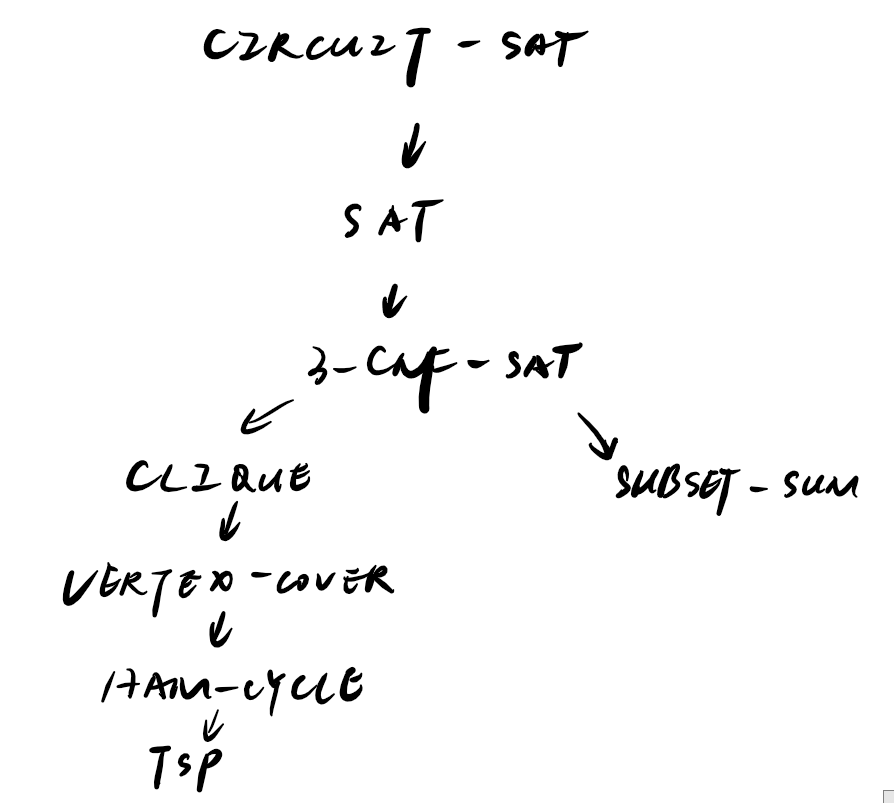
上述问题的证明关系大致是这样的：
-
子图同构问题：两个无向图 \(G_1, G_2\)，\(G_1\) 是否和 \(G_2\) 的某一个子图同构？
-
0-1 整数规划问题：给定 \(m \times n\) 的整数矩阵 A 和一个整数 \(m\) 维向量 b，是否有一个整数 \(n\) 维向量 \(x\)，其取值为 \(0\) 或者 \(1\)，满足 \(Ax \le b\)。
-
整数线性规划问题：\(x\) 的取值为任意整数。其他同上。
-
集合划分问题：输入集合 \(S\)，问是否可以划分为两个集合使得它们的和相等。
-
最长简单回路问题：一个图中找到最长的简单回路。（或者说，子图上的哈密顿路。）
-
独立集问题：求图上最大独立集。
-
图的着色问题：给定无向图，给每个点覆盖一个颜色，使得不存在一对颜色一样的相邻点。求最少使用多少个颜色可以。具体地，判定 3-着色 是 NP 完全问题。
-
二分图完美匹配数。
