括号序列问题
括号序列,是一些由左右括号组成的序列(字符集很小)可以转化为树形结构,或者是一个二维折线图。
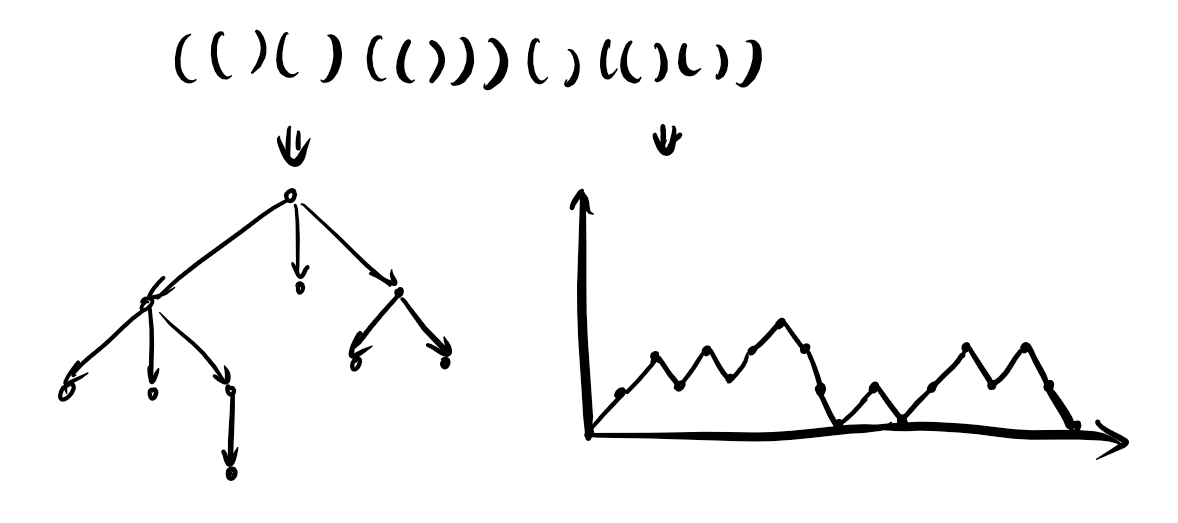
这两种方式各有长处,三种形态变化丰富。其中树的类型其实是给括号定了一个欧拉序。
P8293 [省选联考 2022] 序列变换
【题意】
你手里有一个长度为 \(2 n\) 的合法括号序列 \(s\)。\(s\) 的每一个左括号有一个权值。
在你眼中,不同的括号序列带来的视觉美感不尽相同。因此,你对具有某一种结构的括号序列特别喜欢,而讨厌具有其他一些结构的括号序列。你希望对 \(s\) 进行一些变换,以消除掉一些自己不喜欢的结构。
具体而言,形如 \(\texttt{(A()B)}\)(其中 \(\texttt{A}\)、\(\texttt{B}\) 均为合法括号序列,下同)的结构是你喜欢的,
而形如 \(\texttt{(A)(B)}\) 的结构是你不喜欢的。你有两种操作来改变括号之间的位置。
这两种操作如下:
- 操作 1:交换形如 \(\texttt{p(A)(B)q}\) 的串中 \(\texttt{A}\) 和 \(\texttt{B}\) 之间的两个括号,变换为 \(\texttt{p(A()B)q}\)(其中 \(\texttt{p}\)、\(\texttt{q}\) 为任意串,可以为空,但不一定分别为合法括号序列,下同),它的代价为 \(x\) 乘 \(\texttt{(A)}\) 中第一个左括号的权值加上 \(y\) 乘 \(\texttt{(B)}\) 中第一个左括号的权值,其中 \(x, y \in \{0, 1\}\);
- 操作 2:交换形如 \(\texttt{pABq}\) 的串中的 \(\texttt{A}\) 和 \(\texttt{B}\),变换为 \(\texttt{pBAq}\),这个操作不需要代价。
注意:交换的时候所有左括号的权值是跟着这个括号一起交换的。
你现在想知道的是,将 \(s\) 变换为一个不包含你不喜欢的结构的括号序列至少需要多少代价?
保证 \(2 \le n \le 400000\),\(0 \le x, y \le 1\)。
保证所有的权值在 \([1, {10}^7]\) 之内。
称一个字符串 \(s\) 为合法括号序列,当且仅当 \(s\) 仅由数量相等的字符 \(\texttt{(}\) 和 \(\texttt{)}\) 组成,且对于 \(s\) 的每一个前缀而言,其中 \(\texttt{(}\) 的数量均不少于 \(\texttt{)}\) 的数量。特别地,空串也是合法括号序列。
【分析】
首先很容易想到的是,将括号转成树上结构。然后分析一下操作:对于两个兄弟节点 \(i,j\),做一次操作相当于将 \(j\) 作为 \(i\) 的儿子,并且将 \(j\) 的子树作为 \(i\) 的子树。
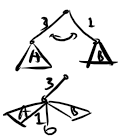
这是表象。接下来分析一下性质。每一次操作是将一个节点下放一个深度,其他节点深度不变。最后要将其变成一条链(换一种说法,每一层留下一个节点)。
注意到 \(x,y\) 的取值影响了花费。
首先一个定序性关键结论:一定是将某一层全部下放再处理下一层。为什么呢?首先它对下一层的操作没有影响:对于某一个节点留下来,那么上面放下来的节点一定都在其儿子上,操作空间/自由度最大。
然后考虑如何最优化权值。我们首先发现 \(x=y=0\) 的情况直接输出 \(0\)。然后思考 \(x=0,y=1\) 的部分分。可以发现权值等于 被下放的节点的下放深度之和,和下放顺序无关。那么显然在每一层留下最大的节点。
接下来看看 \(x=y=1\)。考虑某一层的花费:(这时候和下方顺序有关系)
首先有个策略,对于每一层,是将其他节点(除了留下来的)挂在最小值节点上,然后将最小值挂在留下来的上。(证明:效果都一样,但是你不挂在最小值上就会在 \(x\) 上有损失)容易算出来答案是 \(\sum val + minvalue(size - 2)\)。
注意到将最大值留下一定是好的。不仅之后 \(\sum val\) 小,\(minvalue\) 也小。(\(size-2\) 这个是固定值)
那 \(x=1,y=0\) 的情况就稍微复杂。考虑每一层的花费:
- 留下的节点的一倍花费。
- 最小值的 \((size-2)\) 倍花费。
对其求和,我们发现第一个花费一定加起来等于 \(sum\)!也就是说根本不需要考虑这个值,只需要考虑最小化第二个花费之和(下只考虑这一部分,计算的时候也只需要计算这一部分)。
考虑 \(size\) 的变化,一定是 \(1,...,1,2,...,2,\ge 3,...,\ge 3,3,2,1\) 这样。注意到最早的一段 \(1\) 没有任何抉择余地。之后的花费,除了最后一层是负的,其他都是正的。
考虑全局最小值,一定是从它加入开始一直贡献直到倒数第二层被踢出(牢记贡献的格式!)。这给了我们一个策略的转机。我们希望把最大值留在最后,又希望把最小值传到后面继续用。
先考虑没有那一串 \(3\) 的情况。这时候贡献等于(\(-\)留下来的那个)。显然将最大值传下去,其他都随便传。
有 \(3\) 呢?对于 \(size \ge 3\) 的一段之后的东西,我们仍然有唯一正确的操作:每次取次大值。(这样就算最大值传不到最下面也不会造成任何贡献)如果这个最大值在最后没起到任何效果(不会留在最后)的话,那传最大值不如传最小值。并且可以证明传其他值都没用(如果留在了最后不如用最大值,否则不如用最小值)。
于是模拟即可。
时间复杂度 \(O(n \log n)\)。
【反思】
手玩性质非常重要。并且要向所有方向积极拓展,争取找到新性质。
这题非常多策略。只有你了解了这个题目的全貌,才可以窥见正确的美妙的那个策略。
【实现】
注意到树的结构只和深度有关。因此不需要显式建树,省去 bfs。
Alex_Wei
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 5;
int n, x, y, v[N], stc[N];
char s[N << 1];
vector <int> buc[N];
multiset <int> t;
long long ans, sum;
int main() {
cin >> n >> x >> y >> (s + 1);
for(int i = 1; i <= n; i++) scanf("%d", &v[i]);
for(int i = 1, top = 0, cnt = 0; i <= n << 1; i++)
if(s[i] == '(') stc[++top] = ++cnt;
else buc[top].push_back(v[stc[top]]), top--;
if(x == 0 && y == 0) ;
else if(x == 0 && y == 1) {
for(int i = 1; i < n; i++) {
for(int it : buc[i]) t.insert(it), sum += it;
ans += sum -= *--t.end(), t.erase(--t.end());
}
}
else if(x == 1 && y == 1) {
for(int i = 1; i < n; i++) {
for(int it : buc[i]) t.insert(it), sum += it;
ans += *t.begin() * (t.size() - 2) + sum;
sum -= *--t.end(), t.erase(--t.end());
}
}
else {
static int sz[N] = {1}, mx[N], mn[N], p = 1, q = 1;
memset(mx, 0, sizeof(mx)), memset(mn, 0x3f, sizeof(mn));
for(int i = 1; i <= n; i++) sz[i] = sz[i - 1] + buc[i].size() - 1;
while(p <= n && sz[p] == 1) p++, q++;
while(q <= n && sz[q] == 2) q++;
for(int i = p; i < n; i++) {
if(i != q) mn[i] = mn[i - 1], mx[i] = mx[i - 1];
for(int it : buc[i]) mn[i] = min(mn[i], it), mx[i] = max(mx[i], it), sum += it;
}
long long res1 = sum - mx[n - 1], res2 = sum - max(mx[q - 1], mx[n - 1]); // res1 是下放最小值,res2 是下放最大值
for(int i = q; i < n; i++) res1 += 1ll * (sz[i] - 2) * min(mn[q - 1], mn[i]), res2 += 1ll * (sz[i] - 2) * mn[i];
ans = min(res1, res2);
}
cout << ans << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号