多项式插值

一个 \(n-1\) 次多项式，可以用 \(n\) 个点 \((x_i,y_i)\) 表示。
知道了某个多项式上 \(n\) 个点的点值，可以用拉格朗日插值公式还原出多项式，或者求给定 \(x\) 的函数值。朴素做法时间复杂度 \(O(n^2)\)。可以运用分治+NTT优化到 \(O(n \log n)\)。如果给定要求的点是一个点，并且你可以选择一段有特殊性质的点值（例如 \(x_i = i\)），可以用预处理的方法做到线性快速插值。

基本柿子

\[f(x) = \sum \limits_{i} \cfrac{\prod \limits_{j \neq i} (x-x_j)}{\prod \limits_{j \neq i} (x_i-x_j)} \times y_i \]

根据“第 \(i\) 项点的值为 \(y_i\)，其他为 \(0\)”构造。注意下方为 \(\prod(x_i - x_j)\)，推的时候不要犯迷糊。

显然是一个 \(n-1\) 次多项式。
注意负数。

P4781

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
#define watch(x) cerr  << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
const int mod=998244353;
int qpow(int n,int k){
    int ans=1;
    while(k){
        if(k&1)ans=ans*n%mod;
        n=n*n%mod;
        k>>=1;
    }
    return ans;
}
int x[100010],y[100010];
//调不出来给我对拍！
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    int n,k;cin>>n>>k;
    f(i,1,n)cin>>x[i]>>y[i];
    int ans=0;
    f(i,1,n){
        int tmp=1;
        f(j,1,n){
            if(j==i)continue;
            tmp=tmp*(k-x[j])%mod+mod;tmp%=mod;
            tmp=tmp*qpow(x[i]-x[j],mod-2)%mod+mod;tmp%=mod;
        }
        tmp=tmp*y[i]%mod;
        ans=ans+tmp;
        ans%=mod;
    }
    cout<<ans<<endl;
    //time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}

快速求点值

如果是单点求值，并且自由选点，那么选择 \(x_i = i\)，原式可以预处理前缀后缀相关柿子做到每一项 \(O(1)\) 计算。

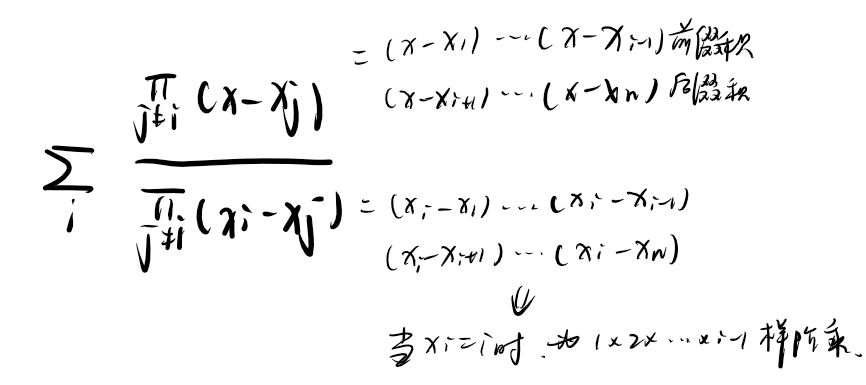
例题

【题意】
求

\[\sum \limits_{i=1}^n i^k \]

其中 \(n \le 10^9, k \le 10^6\)

---

【分析】
首先有个观察得到的性质，\(k\) 次方和是 \(k+1\) 次多项式。

然后前 \(k+1\) 项可以递推得到。

于是插值可以做。