ARC153 ABC 题解

A

【题意】
给定 $N$，求第 $N$ 个满足以下条件的数：

• 它是一个 $9$ 位数，没有前导 $0$。
• 它的第一位等于它的第二位。
• 它的第五位等于它的第六位。
• 它的第七位等于它的第九位。

例如 $998244353$。

保证存在第 $N$ 个这样的数。

---

【分析】
本质不同的数只有 $10^6$ 个。可以直接枚举。

也可以按位直接求，显然第 $\mathtt{ABCDEF}$ 个满足条件的数是 $\mathtt{(A+1)(A+1)BCDDE(F-1)E}$。

B

【题意】
给定 $N\times M$ 的字符矩阵。做 $Q$ 次操作，每次形如把矩阵竖着和横着切两刀，形成的四个区域分别翻转 $180°$。

求操作之后的矩阵。

$N,M,Q \le 2 \times 10^5$

---

首先考虑一维怎么做。手玩一下如下图：（我们只关心每个位置最后跑哪里去了，不妨设 $c_i = i$）

注意到不管怎么翻转，都是一个 $1 \sim 7$ 正或反着循环放在某一个位置上。进一步地，如果操作次数为奇数，那么是反的。否则是正的。位置怎么考虑？考虑追踪 $1$ 和 $7$ 的分界线，不难发现进行左端点为 $x_1,x_2,...,x_k$ 的操作之后，它在什么位置上：
$x_1-x_2+...+x_k$（$k$ 为奇数）
$-x_1+x_2+...+x_k$（$k$ 为偶数）

然后就能做一维的情况了。

接下来推广的时候我们会发现两维之间是独立的，根本不需要其他什么考虑就可以推广了。

因此我们得到了一个做法：每一维分别考虑，每一维只需要维护形如 $x_1-x_2+...+x_k$ 的一个数，最后按顺序放置标记位置的数字即可。

时间复杂度 $O(NM + Q)$。

C

【题意】给定数列 $A_1,A_2,...,A_n$，其中每个数都是 $1$ 或者 $-1$。试图构造 $B_1,B_2,...,B_n$ 使得 $B$ 严格递增并且 $\sum \limits_{i = 1}^{n} A_i B_i = 0$。

---

先给 $B$ 随便赋值，然后调整一下。

考虑随便赋值之后，得到的数是 $k$。我们可以给某一个前缀减去某个数，或者给后缀加上某个数，使得总共变化了 $-k$。如下图所示。

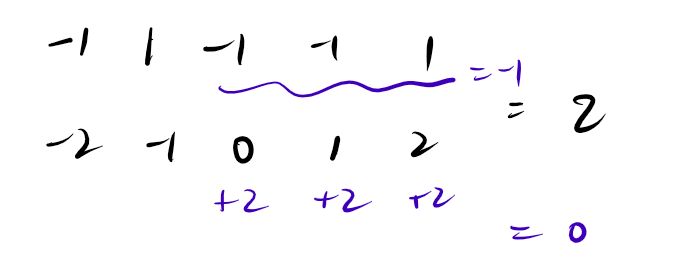
令选出的位置的 $A$ 之和为 $t$。不难发现 $t$ 取 $1$ 或者 $-1$ 的时候是最好的（灵活性最大，并且限制也最少）。

如果 $k>0$，需要总共加上一个负数。那么可以选择一段 $t = 1$ 的前缀，给它们分别减去 $k$；或者选出一段 $t=-1$ 的后缀，给它们分别加上 $k$。

$k<0$ 同法。

如果选不出来怎么办？其实这些情况都是无解的。考虑证明。

因为选不出来的串首先长度是偶数，其次形如下面这样的数列，可以让 $1$ 表示左括号或者右括号，$-1$ 表示另一种括号，得到一个合法括号序列。

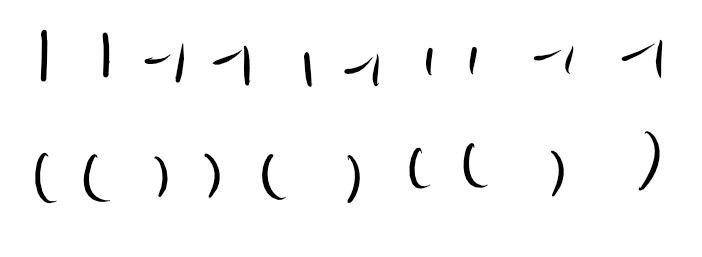
我们会发现这样的时候选不出 $<0$ 的前缀，也选不出 $>0$ 的后缀。

其实我们考虑一一匹配的括号。不妨考虑左括号是 $1$，右括号是 $0$ 的情况。令一对匹配括号的下标是 $i,j$。这时候由于 $B$ 数组左边永远比右边小，因此 $B_iA_i = B_i < B_j= -B_jA_j$。

因此这样得出来的一定是个小于 $0$ 的数，因为每一对数字加起来都小于 $0$。

因此有解构造，无解输出就行。