AC自动机

简介

AC 自动机是对多模式串压缩 LCP 形成的结构。其每一个节点代表了这些模式串的一个前缀。其 fail 树上父亲是儿子的后缀。因此前缀和后缀匹配的问题可以考虑 AC 自动机。

AC 自动机之于 KMP 类似广义 SAM 之于 SAM，都是在 trie 上做一个自动机。

AC 自动机的结构

是在一个 trie（每一个节点有若干个普通边）上，增加了一些 fail 指针，fail 指针对于每一个节点只有一个，其含义是指向所有前缀里，这个节点代表的前缀的最长后缀。特别地，起始点 \(1\) 认为是空串，是任意字符串的前缀；认为 \(fail_1 = 0\)，而 \(0\) 走任何普通边均到达 \(1\)。（这是为了统一需要）

首先在有主串进行匹配的时候，如果这个点失配，那么可以认为是跳到 fail 然后再进行匹配；然后这些 fail 形成了一棵树，其中每一个节点代表的前缀都是其所有子孙的后缀。如果有一个串在 AC 自动机上跑匹配，经过了某一个点相当于出现了其和其所有祖先：

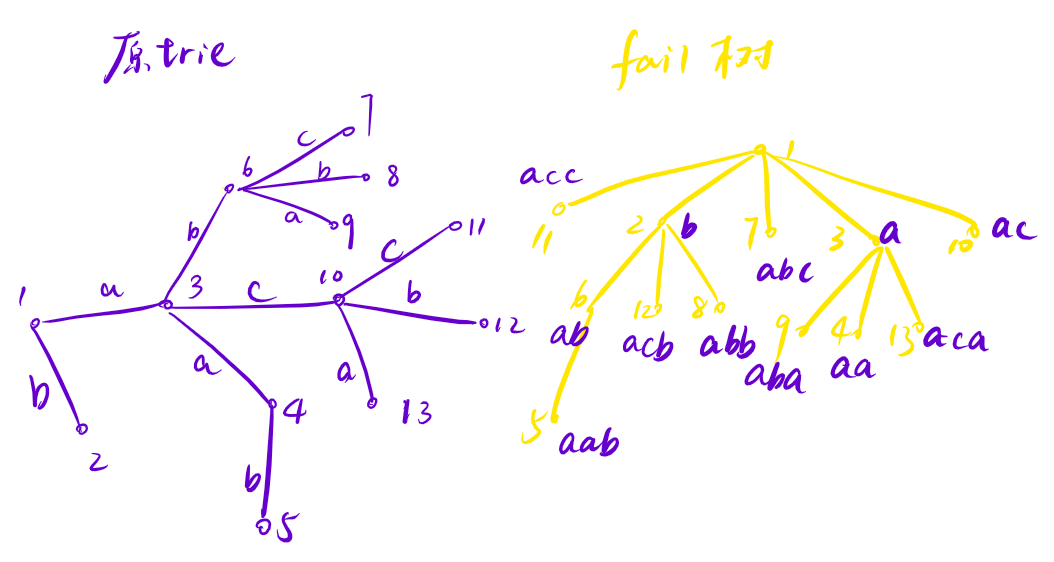
对于 fail 树，它和后缀树一样都很有用：某一个点的子树代表了所有以它为后缀的前缀（或者说，如果认为根到 trie 树上每个点都是一个字符串，那么拥有某一个后缀的所有字符串都在这个后缀所代表的点的子树上）

在 AC 自动机上，可以跑 dp，类似在 DAG 上 dp，有关匹配的都可以 dp。dp 状态形如：目前到了哪一个点。停止的时候，也可以借助 trie 树进行合并。

构造

考虑这个 fail 怎么建。如果直接建肯定是不行的。但是你考虑某一个串 \(sa\)，\(s\) 是字符串，\(a\) 是字符，如果 \(s\) 的 fail 有连向 \(a\) 的边，那么这个边连到的点就是 \(sa\) 的 fail。否则再看 \(s\) 的 fail 的 fail 有没有连向 \(a\) 的边，...

最后到了空串的时候一定停止。

那我们考虑如果某一个点 \(i\) 没有 \(a\) 边，不妨令 \(a\) 边连向 \(fail_i.edge_a\)。如果这么做，那么 \(fail_{fa_i}.edge_a\) 一定就是 \(i\) 的 fail 了。或者说，\(fail_i.edge_a\) 可以认为意义是 \(i\) 这个状态如果再加入一个字符 \(a\)，除了走自己的 \(a\) 边之外，会走到哪里。

我们就是这样建 fail。那么起始位置的时候会发生什么事？如果起始位置连出去一条 \(a\) 边，走到点 \(i\)，那么按照刚刚的方式 \(fail_i\) 会到达 \(fail_1.edge_a\)，这就是为什么我们令 \(fail_1 = 0, 0.edge_* = 1\)。

这是一个递推建立，时间复杂度是 \(O(n |\sum|)\)，递推建立就需要有拓扑序，需要 fa 处理好了，因此我们 BFS 构造即可。这是一个静态建立的过程，而不是动态插入。

struct node {
    int to[26], fail;
};
struct ACAM {
    node a[2001000]; 
    void build(){
        queue<int> qq; qq.push(1); 
        f(i,0,25)a[0].to[i]=1;
        while(!qq.empty()) {
            int now=qq.front();qq.pop();
            f(i,0,25) {
                if(a[now].to[i]) {
                    qq.push(a[now].to[i]);
                    int nxt = a[now].to[i];
                    a[nxt].fail = a[a[now].fail].to[i];
                }
                else a[now].to[i] = a[a[now].fail].to[i];
            }
        }
    }
}ac;

（我们认为在运行 build 之前已经建立好正常的一棵 trie 树，以 \(1\) 为根）

P3796

【题意】
给定一些模式串和一个文本串，求每一个模式串在文本串中出现几次。

【分析】
首先我们在 ac 自动机上把文本串跑一遍（直接用 to 边即可，因为 to 边的特殊含义这张图变成了一个闭合子图）

然后某一个点某时刻走到某一个节点的时候，其所有祖先都相当于出现了一次，所以最后在 fail 树统计子树的出现次数和即可。

P6257 [ICPC2019 WF]First of Her Name

【题意】
给定一棵 trie 树，树上每一个点都代表着根到这个点经过路径中字符顺次相接形成的字符串。给定一些询问，每个询问一个字符串，求这些字符串中有多少个的后缀是询问串。

【分析】
刚刚说到后缀树上某个点的子树是统计这个的，但是如果直接对 trie 建 AC 自动机那么不一定有一个点就是询问串。所以把询问串也拉进来建 AC 自动机即可。

#include<bits/stdc++.h>
using namespace std;
//#define int long long
//use ll instead of int.
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr  << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
    string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; } 
    reverse(s.begin(), s.end()); cerr << s << endl; 
    return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍！
//use std::array.
char c[1001000]; int p[1001000]; string q[1001000]; int ans[1001000];
int n, k;int mid = 0;
struct node {
    int to[26], fail;
    vector<int> que; 
};
struct ACAM {
    node a[2001000]; 
    int cnt = 1; 
    void build(){
        queue<int> qq; qq.push(1); 
        f(i,0,25)a[0].to[i]=1;
        while(!qq.empty()) {
            int now=qq.front();qq.pop();
            f(i,0,25) {
                if(a[now].to[i]) {
                    qq.push(a[now].to[i]);
                    int nxt = a[now].to[i];
                    a[nxt].fail = a[a[now].fail].to[i];
                }
                else a[now].to[i] = a[a[now].fail].to[i];
            }
        }
    }
}ac;
vector<int> t[2000200];
int occ[2000200];
void dfs(int now) {
    if(now <= mid && now >= 2) occ[now] = 1;
    for(int i : t[now])  {dfs(i); occ[now] += occ[i];}
    for(int i : ac.a[now].que) ans[i] = occ[now];
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
     cin >> n >> k;
    f(i,1,n)cin>>c[i]>>p[i];
    f(i,1,k)cin>>q[i];
    f(i,1,k)reverse(q[i].begin(),q[i].end());
    ac.build(); 
    for(int i=1;i<=ac.cnt;i++)t[ac.a[i].fail].push_back(i);
    dfs(1);
    f(i,1,k)cout<<ans[i]<<endl;
    return 0;
}
*/