上下界网络流
上下界网络流,就是每条边既有流量上界也有流量下界的网络流。分为无源汇上下界可行流、有源汇上下界最大流、有源汇上下界最小流三种。
我们回顾网络流模型的两个关键要素:流量守恒和容量限制。流量守恒是除了源点和汇点之外点的总流量均为 \(0\) 的限制,而容量限制则是对每条边加了一个限制:不仅要小于一个 \(c_上\),还要大于一个 \(c_下\)。
想象之前学的最大流模型都是有源点汇点,并且求的最大流是源点流出的流量最大值。没有源点和汇点的时候,每个点流量都为 \(0\)。没有下界的时候图可以静如死水,也就没有什么最大流一说了。加了下界之后,网络流这张图不可以静如死水,可能必须要动起来了。这时候我们就遇到了一个问题,需要求出一个可行流。
例如这样,用 \([c_{下},c_上]\) 表示上下界,红色标注是一个可行流。
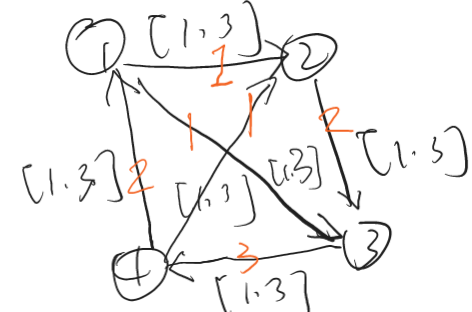
加上源点汇点之后,我们同样有求最大流环节;并且由于加上了上下界,我们还有求最小流环节。
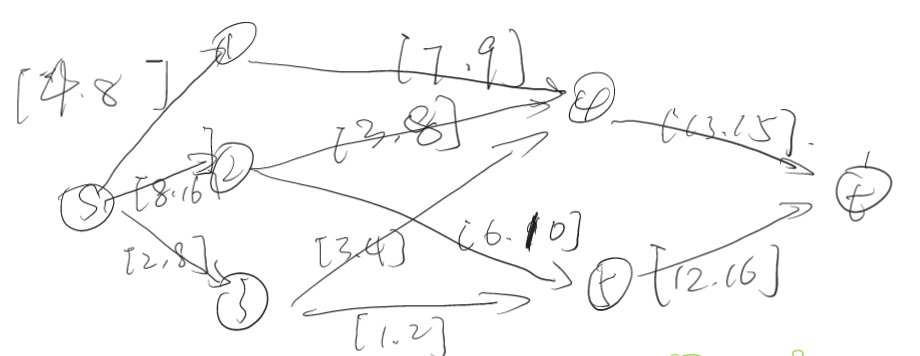
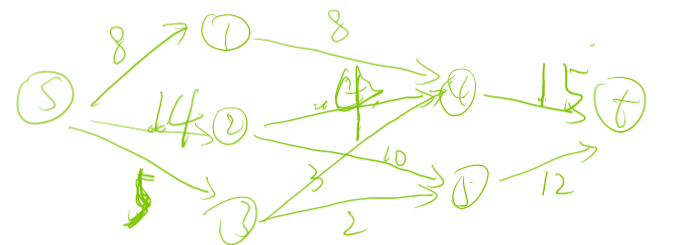
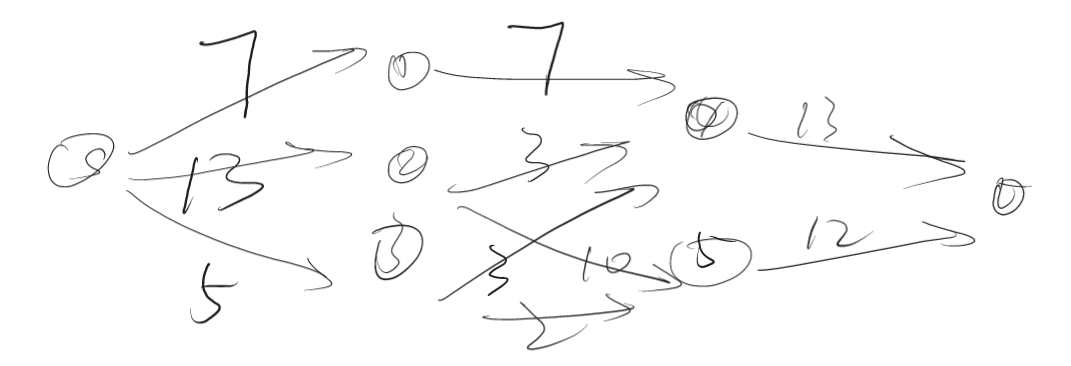
例如这张图,最大流和最小流分别为如下两张图:
接下来我们具体讨论这三种问题怎么解决。
无源汇上下界网络流
上下界网络流是没法维护的,我们基本的想法是要把它转化为只有上界。考虑对于一条边,我们把流量和容量都减去 \(c_下\),然后最后还原的时候复原。
这样做会有一个什么错误呢?容量限制依然满足,但是流量不守恒了!这是因为,每个点删掉的出边和入边下界和之差不一定是 \(0\)。假设所有入边下界之和为 \(c_入\),出边下界之和为 \(c_出\)。原流量为 \(0\) 的点如今流量(流出-流入)为 \(c_入 - c_出\)。
这怎么办?我们其实可以考虑建立一个虚拟的源点,补充消失的流量。也就是说,要求 \(s\) 对该点有 \(c_入 - c_出\) 的流量。如果是负数,要求该点对 \(t\) 有 \(c_出 - c_入\) 的流量。
怎么处理新加流量?其实直接加为容量求最大流就好了,并且要求这个最大流必须满流。也就是说,\(s\) 连出去的每一条边都必须满流,\(t\) 连进来的每一条边都必须满流。这两个一定同时达到,因为 \(\sum \limits_{i} c_入 - c_出 = 0\)。
考虑该做法的正确性:对于新图 \(G'\)(唯一确定)和新图的一个最大流 \(f'\),对最大流只取出中间部分,每条边加上原有的下界,依然保持容量限制和流量守恒。
另外,原图的每一个可行流和新图的每一个最大流一一对应。这个不证明了。
有源汇上下界最大最小流
考虑存在源点和汇点的情况。这种情况下,我们先建一条 \(t \rightarrow s\),容量为 \(+\inf\)。然后变成无源汇上下界可行流,先求出一个可行流再说。然后直接在这个可行流上抓出原图,在残量网络上直接跑 \(s \rightarrow t\) 或者 \(t \rightarrow s\) 的最大流(取决于题目问的是最大还是最小流)。
这个为什么是对的?考虑增广路定理:对于原图 \(G\) 的一个流 \(f\),如果原图上不存在增广路,那么 \(f\) 是最大流。
那么这张图里呢?求出的流 \(f\) 是新图里的,甚至不是原图的可行流。(\(S,T\) 流量不守恒)但是我们把新图里的任意一个在 \(f\) 上寻找若干条 \(s \rightarrow t\) 的增广路得到的图中 \(t \rightarrow s\) 的那条新增边上的流量 \(f'\) 减去 \(f\),得到的是一个 \(s \rightarrow t\) 的可行流。为什么呢?
证明:首先 \(S,T\) 满流,因此减掉之后 \(S,T\) 流量不仅守恒,而且不存在流量。这样图的范围就缩减为原图的了。接着看每条边的流量。显然是增广路上的流量,所以是可行的。然后 \(s,t\) 两个点如果看成之前的无源汇,那么 \(t \rightarrow s\) 减去增广路上的对应流量即可,还是一个无源汇可行流。如果看成原图上的有源汇,那么是正常的退流/加流操作。
由于 \(|f|\) 固定,所以只需要找到一个最大的新增边上的流量 \(|f'|\) 即可。(关键边思想)
这里来一张求最小流的图,看的比较清楚。
原图:
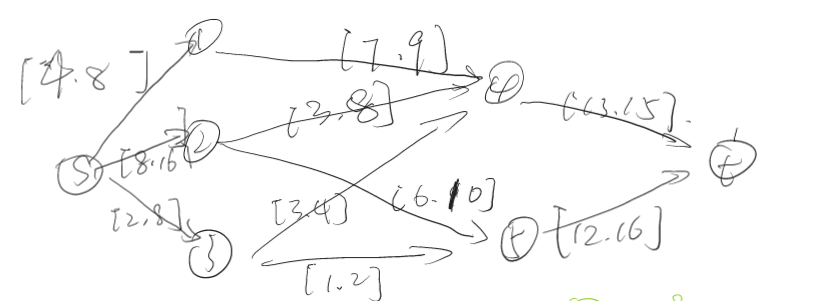
新图:
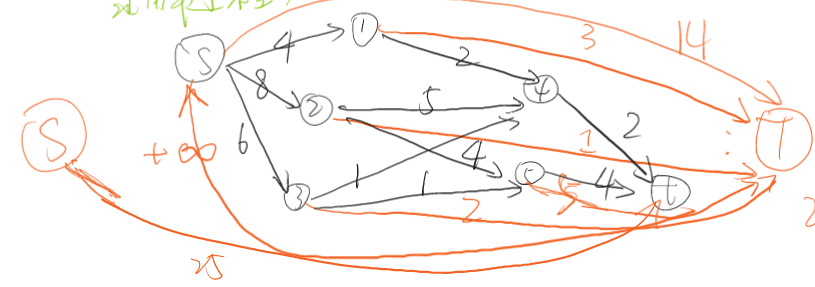
找到的一个满流:
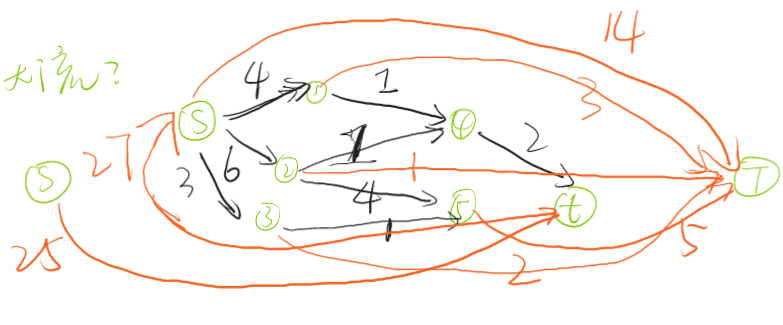
dinic的结果:
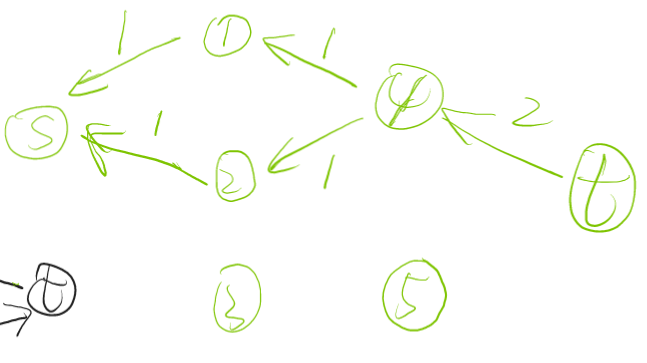
最小流:

【模板】
无源汇上下界可行流:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
int head[220], nxt[(220 + 10220) * 2], to[(220 + 10220) * 2], cap[(220 + 10220) * 2]; //cap = c - f
int sum[220]; //c_入-c_出
int cd[(220 + 10220) * 2];
int cur[220];
int dep[220];
int s = 0, t = 201, cnt = -1;
void add(int a,int b,int c,int d) {
nxt[++cnt] = head[a]; to[cnt] = b; cap[cnt] = d - c; sum[a] -= c; cd[cnt] = c; head[a] = cnt;
nxt[++cnt] = head[b]; to[cnt] = a; cap[cnt] = 0; sum[b] += c; cd[cnt] = 0; head[b] = cnt;
}
bool bfs() {
memset(dep, -1, sizeof(dep));
queue<int> q; dep[s] = 0; cur[s] = head[s];
q.push(s);
while(!q.empty()) {
int now = q.front(); q.pop();
for(int i = head[now]; ~i; i = nxt[i]) {
if(cap[i] > 0 && (dep[to[i]] == -1)) {
dep[to[i]] = dep[now] + 1; cur[to[i]] = head[to[i]];
q.push(to[i]);
if(to[i] == t) return 1;
}
}
}
return 0;
}
int dfs(int now, int limit) {
if(now == t) return limit;
int flow = 0;
for(int i = cur[now]; ~i && flow < limit; i = nxt[i]) {
cur[now] = i;
if(dep[to[i]] == dep[now] + 1 && cap[i] > 0) {
int tmp = dfs(to[i], min(cap[i], limit - flow));
if(!tmp) {dep[to[i]] = -1;}
flow += tmp; cap[i] -= tmp; cap[i ^ 1] += tmp;
}
}
return flow;
}
int dinic() {
int maxflow = 0, flow = 0;
while(bfs()) {
flow = dfs(s, inf); maxflow += flow;
}
return maxflow;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n,m;cin>>n>>m;
t = n + 1;
memset(head, -1, sizeof(head));
f(i,1,m){
int a,b,c,d;cin>>a>>b>>c>>d;
add(a,b,c,d);
}
int full = 0;
vector<int> tick;
f(i,1,n){
if(sum[i]>0){add(s, i, 0, sum[i]); tick.push_back(cnt); full += sum[i];}
else if(sum[i] < 0) {add(i, t, 0, -sum[i]);}
}
dinic();
int lluf = 0;
for(int i : tick) lluf += cap[i];
if(lluf < full) {cout << "NO\n"; return 0;}
else {cout<< "YES\n";}
for(int i = 1; i <= 2 * m - 1; i += 2) {
cout << cd[i ^ 1] + cap[i] << endl;
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
有源汇上下界最大最小流:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
int S, T;
int head[220], to[(10010 + 220) * 2], nxt[(10010 + 220) * 2], cap[(10010 + 220) * 2];
int cur[220], sum[220], dep[220];
int cnt = -1;
int cd[(10010 + 220) * 2];
void add(int a, int b, int c, int d) {
nxt[++cnt] = head[a]; to[cnt] = b; cap[cnt] = d - c; head[a] = cnt; cd[cnt] = c;
nxt[++cnt] = head[b]; to[cnt] = a; cap[cnt] = 0; head[b] = cnt; cd[cnt] = 0;
sum[a] -= c; sum[b] += c;
}
bool bfs() {
memset(dep, -1, sizeof(dep));
queue<int> q; q.push(S); cur[S] = head[S]; dep[S] = 0;
while(!q.empty()) {
int now = q.front(); q.pop();
for(int i = head[now]; ~i; i = nxt[i]) {
if(cap[i] && (dep[to[i]] == -1)) {
dep[to[i]] = dep[now] + 1; cur[to[i]] = head[to[i]];
q.push(to[i]);
if(to[i] == T) return 1;
}
}
}
return 0;
}
int dfs(int now, int limit) {
if(now == T) return limit;
int flow = 0;
for(int i = cur[now]; ~i && flow < limit; i = nxt[i]) {
cur[now] = i;
if(dep[to[i]] == dep[now] + 1 && cap[i] > 0) {
int tmp = dfs(to[i], min(cap[i], limit - flow));
if(tmp == 0) {dep[to[i]] = -1;}
cap[i] -= tmp; cap[i ^ 1] += tmp; flow += tmp;
}
}
return flow;
}
int dinic() {
int maxflow = 0, flow;
while(bfs()) {flow = dfs(S, inf); maxflow += flow;}
return maxflow;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n,m,s,t; cin >> n >> m >> s >> t;
memset(head, -1, sizeof(head));
S = 0, T = n + 1;
f(i, 1, m) {
int a, b,c,d;cin>>a>>b>>c>>d;
add(a,b,c,d);
}
vector<int> tick;
int full = 0;
f(i, 1, n) {
if(sum[i] > 0) {full += sum[i]; tick.push_back(cnt); add(S, i, 0, sum[i]);}
else if(sum[i] < 0) {add(i, T, 0, -sum[i]);}
}
add(t, s, 0, inf); int adb = cnt;
int lluf = dinic();
int ans = cap[adb];
// cout << ans << endl;
// cout << full << endl;
// int lluf = 0;
// for(int i : tick) {
// lluf += cap[i];
// }
// cout << lluf << endl;
if(lluf < full) {cout << "No Solution" << endl; return 0;}
else {
S = s; T = t;
cap[adb] = cap[adb ^ 1] = 0;
ans += dinic();
}
cout << ans << endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}


