SAM(后缀自动机)
简介
字符串处理问题中,有模式串和文本串。会考察模式串在文本串中的出现情况(匹配了多少个/最长匹配前缀是多少/...)当我们确定了模式串的时候,可以用 KMP 算法进行求解,也可以使用哈希算法解决部分问题。如果模式串较多(或者直接看成一棵 trie),可以对模式串们建立 AC 自动机,其是一个对模式串压缩 LCP 之后的结构,在 trie 的基础上建立,于是可以解决一些前缀问题。其 fail 树满足后缀一致性,可以解决少量后缀问题。也可以对主串建立后缀自动机,在这上面做有关问题。后缀自动机的 link 树也是一个性质很好的结构。如果主串是 trie,也可以建立广义后缀自动机,也就是 trie 上的自动机。
所有子串全部存下来放在一个 DFT 里,这个 DFT 有一个起点,其他都是终点。
像这样。
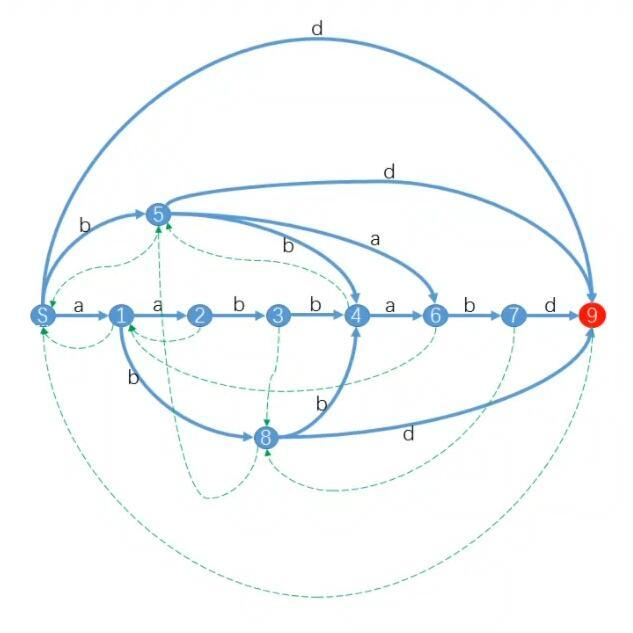
性质
- 任何一条从 S 节点出发走普通边到一个其他节点所经过的路径上的字符组成的字符串,都和原串中的一个子串一一对应。(不重不漏)
- 一个除了 S 之外的节点有三个属性:第一个是 \(len\),是记录这个节点上子串的一个特征的,之后再说,第二个是普通边(\(edge\),简称 \(ed\)),每个节点可以向外连一个普通边。一个节点向外连出一个普通边,表示节点表示的字符串后面加上一个字母。第三个是 \(father\) 边(或者叫 \(link\) 边)。每个节点有且仅有一条 \(father\) 边并且一定往回连,这些 \(father\) 边组成一棵反向树,\(father_i\) 就是正常的树中 \(i\) 的父亲。
- (重要)每一个点表示若干个原串中的子串,这些子串都是从 S 开始经过某个路径到达这个点的。记这些子串的集合为 \(\{U\}\)。那么所有 \(\{U\}\) 中子串在原串中所有出现位置是一样的。并且每一个串都是最长串的后缀,\(\{U\}\) 中每个字符串都长度不同。证明:对于串 \(i\),考虑 \(|i| < |j|\),如果串 \(j\) 是它的后缀,那么 \(j\) 出现的位置都会出现 \(i\);否则都不会出现 \(i\)。
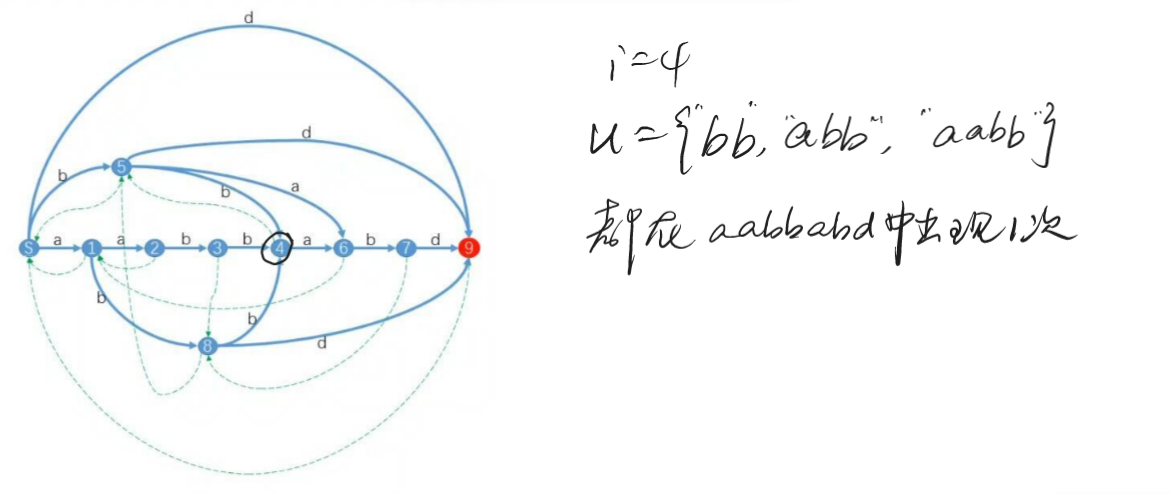
- 建出来的树叫做 \(father\) 树,满足子节点的出现位置都是父节点的真子集,并且不会有交集(如果不是相同,就一定无交集,和上面证明一个道理)。其子节点集合的并集,并上所有父节点表示的子串中是前缀的终止位置集合,等于父节点集合。如下图:
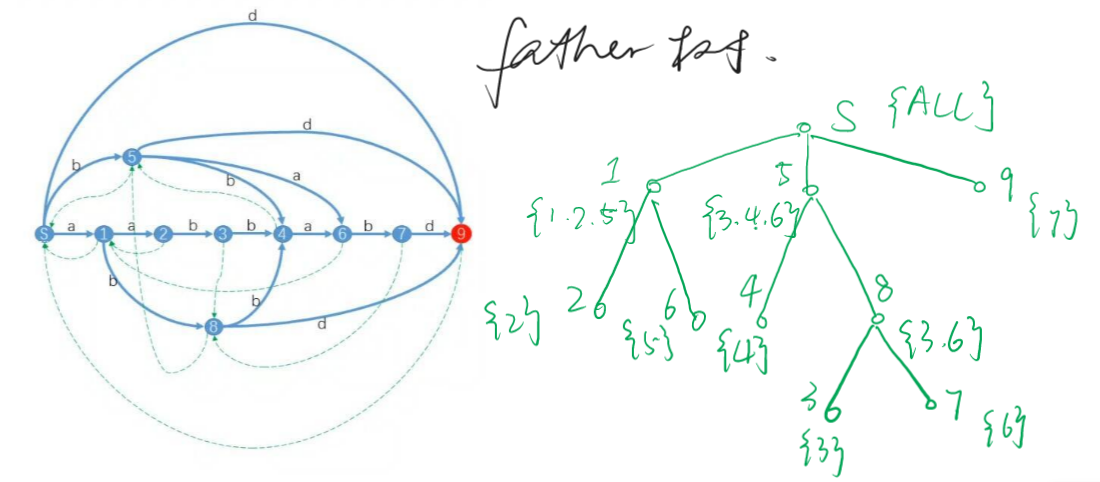
可以发现消失掉的数字都是前缀。 - \(len\) 数组记录的就是 \(\{U\}\) 中最长串长度。最短串长度不用记录,就是父节点的最长串长度 \(+1\)。
- 一个节点想要跳转到其前面去掉一个字母的后缀,就看其是否为最短串。如果是,跳到父亲节点。否则,还在自己。如果要跳到一个前缀,那么记录返回边即可。
- 规模方面,点数 \(O(|s|)\),边数 \(O(|s|)\)。(边数方面和广义 SAM 不一样,广义 SAM 是 \(O(|s||\sum|)\) 的。)
构造方式
采用动态插入字符的方式。
考虑插入一个字符之后,自动机的结构会发生什么变化。在具体考虑之前,重申一下,自动机维护的是一些 endpos 集合相同的子串,他们是长度相邻的一些后缀。link 边前往的是由于后缀的长度比较小而增加了一些 endpos 的等价类。
好。我们现在在某一个字符串的后面增加了一个字符 \(c\)。看看哪些东西会变。
首先,增加了一些子串。显然只有后缀会新增。然后我们从最长的后缀 \(p\) 点开始一直跳 link,并且对 \(p\) 点增加 \(c\) 普通边,直到这个点存在这个字符的普通边。这个过程就是不断缩小后缀的长度,直到后缀足够短的时候就已经出现过了。容易发现如果某一个后缀出现过了,其后缀一定也出现过了。所以不需要再添加了。
然后是有可能出现一些等价类的重新划分,以及怎么连 link 的问题。可以结合 aabbabd 这一个串记忆。(这个串就是很典型的一个了,需要记下来)
考虑加上第二个 b 的时候,前面 aabba,abba,bba,ba 都只在后缀位置出现过,但是 a 在前面出现了三次。其是一个等价类。然后它沿着 b 普通边走到集合 \(q = \{ab, aab\}\),他们的 endpos 都只有 \(3\)。但是加上这个 b 之后,ab 和 aab 显然不在一个集合内了,断开为了两个集合:其中一个集合是 aabbab 的后缀,而另一个不是。可以发现第一个集合的 len = p.len + 1(此时 p 是 a 的集合),出现次数增加了。另一个集合的 len 等于集合 q 的 len,出现次数没有增加。这种情况下,建立一个 nq 表示第一个集合,q 转而表示第二个集合,np 的 link 应该在 nq,而 q 的 link 也在 nq。需要改变 nq 的 len,其他和 q 一样。p 的普通边需要转向 nq,而 p 的后缀如果先前连向 q 的,也要转向 nq。
这就是最复杂的一个情况,一共有四行更改语句,其中一行是一个 while,一行同时修改了两个 fa:
int nq = ++cnt;
dian[nq] = dian[q];
dian[nq].len = dian[p].len + 1;
dian[q].fa = dian[np].fa = nq;
for(; dian[p].ed[c] == q; p = dian[p].fa) dian[p].ed[c] = nq;
void extend(char ch) {
int p = lst;
int np; np = lst = ++cnt;
a[np].len = a[p].len + 1;
tms[cnt] ++;
for(; p && !a[p].g[ch - 'a']; p = a[p].fa) {
a[p].g[ch - 'a'] = np;
}
if(!p) a[np].fa = 1;
else {
int q = a[p].g[ch - 'a'];
if(a[q].len==a[p].len +1){
a[np].fa=q;
}
else {
int nq=++cnt;a[nq]=a[q];
a[nq].len=a[p].len+1;
a[np].fa=a[q].fa=nq;
for(; p && a[p].g[ch-'a']==q; p = a[p].fa){
a[p].g[ch-'a']=nq;
}
}
}
}
记录任意一个子串出现次数
在 \(father\) 树上 DFS,别忘了加上每一个前缀 \(1\) 的贡献。
字典序第 k 小的子串
在后缀自动机这个 DAG 结构上可以方便进行 dp,对于某个点转化为从该点出发的路径数量问题,很容易预处理。然后查询的时候沿着结构走一下即可,单次查询时间是 \(O(len)\) 的,其中 \(len\) 为答案长度。
某子串最早出现位置什么的
在 parent 树上隐式地维护了所有节点的 endpos 集合,需要什么的话直接显式取出就好了。
CF235C. Cyclical Quest
给定 \(s\) 以及 \(n\) 组询问,每组询问给定 \(t\),求 \(s\) 的哪些子序列和 \(t\) 同构。
其中 \(a,b\) 同构定义为,\(a\) 进行循环右移若干位之后和 \(b\) 相等。
建出 SAM。
考虑怎么在 SAM 中找到删去子串前缀一个字母之后的位置。考虑一个字符串 \(k\),对应 SAM 上节点 \(i\)。如果 \(fa_i.maxlen = |k| - 1\) 存在,那么 \(k\) 删去前缀一个字母之后跳到 \(fa_i\)。否则留在 \(i\)。这是后缀自动机的性质保证的。
循环右移,考虑断环为链。记 \(|t| = m, t' = t + t\)。考虑对于 \(i \in [0, m)\),找到该串的出现次数。但是不一定对于每一个 \(t'_{[i, i + m - 1]}\) 能找到一个节点。于是我们用一个双指针 \(i,j\),如果不能再找或者长度到达了 \(m\),就 \(i\) 向右移一位(去除前缀一个字母)。否则 \(j\) 向右移一位(沿着自动机上的边走)即可。
\(t'\) 里可能有些长度为 \(m\) 的子串是重复的,也就会重复计算。这种情况在 \(t\) 包含周期的时候出现。考虑处理 \(nxt\) 数组知道周期,然后 \(i \in [0, T)\) 即可。
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
string s;
int cnt = 1, lst = 1;
int tms[2000010];
struct node {
int len, fa;
int g[26];
}a[2000010];
vector<int> t[2000100];
void extend(char ch) {
int p = lst;
int np; np = lst = ++cnt;
a[np].len = a[p].len + 1;
tms[cnt] ++;
for(; p && !a[p].g[ch - 'a']; p = a[p].fa) {
a[p].g[ch - 'a'] = np;
}
if(!p) a[np].fa = 1;
else {
int q = a[p].g[ch - 'a'];
if(a[q].len==a[p].len +1){
a[np].fa=q;
}
else {
int nq=++cnt;a[nq]=a[q];
a[nq].len=a[p].len+1;
a[np].fa=a[q].fa=nq;
for(; p && a[p].g[ch-'a']==q; p = a[p].fa){
a[p].g[ch-'a']=nq;
}
}
}
}
void dfs(int now) {
for(int i : t[now]) {
dfs(i);
tms[now] += tms[i];
}
}
int ans;
int nxt[1000100];
void deal(string q) {
f(i, 0, (int)q.size() - 1) nxt[i] = 0;
for(int i = 1, j = 0; i < (int)q.size(); i ++) {
while((q[i] != q[j]) && j) j = nxt[j - 1];
if(q[i] == q[j]) {
nxt[i] = ++j;
}
}
int k = q.size();
int len = k - nxt[k - 1]; if(k % len != 0) len = k;
q += q;
int cur = 1;
for(int i = 0, j = 0; i < len; i ++) {
while(j - i + 1 <= k) {
char ch = q[j];
if(a[cur].g[ch - 'a']) {
cur = a[cur].g[ch - 'a'];
j ++;
}
else {
break;
}
}
if(j - i + 1 == k + 1) {
ans += tms[cur];
}
int ls = a[cur].fa;
if(cur == 1 || a[ls].len != (j - i - 1)) {
continue;
}
else {
cur = a[cur].fa;
continue;
}
}
cout << ans << endl;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> s;
f(i, 0, (int)s.size() - 1) extend(s[i]);
f(i, 1, cnt) {
t[a[i].fa].push_back(i);
}
dfs(1);
int m; cin >> m;
f(i, 1, m) {
string q; cin >> q; ans = 0; deal(q);
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
也可以不处理 \(nxt\),因为每个节点表示的长度固定的字符串唯一,因此没有重复当且仅当长度为 \(m\) 的时候走到的节点是第一次走过。
哈希做法,考虑随机给 \(a \sim z\) 赋一个权值,然后加起来做 sum-hash。可能能过?我不好说。


