竞赛图
爹们,这是一月份写的,写的不好别骂了。
竞赛图,是每两个点之间都有一条有向边的图。因为有一种模型是两者之间比赛谁能赢,赢的人对输的人连一条边,因此叫做竞赛图。
竞赛图的性质:
- 对 SCC 缩点之后是一条链式结构,类似下图。对图拓扑排序之后,标号靠前的点都会向标号靠后的点连一条边。这条边的意义是,两个连通分量中分别任意挑出一个点,其间连边方向都和这条边相同。
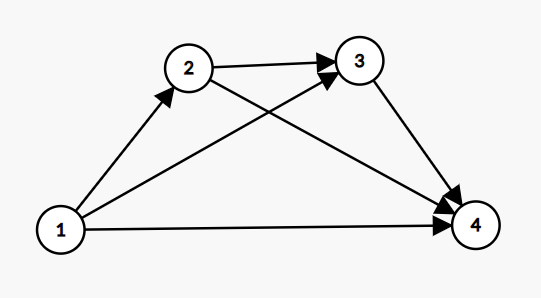
1.1. 对度数排序之后,任意一个连通分量都对应一段连续的点。
我们拿任意一个连通分量举例。假设连通分量内有 \(k\) 个点,拓扑序比它靠前的点有 \(n\) 个,拓扑序比它靠后的点有 \(m\) 个。那么这个连通分量内任意一个点向连通分量外连边的数量都为 \(m\)。考虑连通分量内互相连的点。由于在连通分量内,不会有一个点对其他点的连边都是同一个方向的(除非这个连通分量只有一个点,那样也容易证明是正确的)所以显然成立。
1.2. 我们可以对度数排序后的点分段得到每个连通分量包含的点,具体而言,假设当前还有 \(n\) 个点没有分到连通分量。我们从度数最大的点开始,进行扫描,然后如果扫到第 \(k\) 个点的时候发现度数和为 \(k(n-k)+\cfrac{k(k-1)}{2}\),那么已经扫描到的点属于同一个连通分量,之后的点都不属于这个连通分量。
因为向外连边的条数是固定的 \(k(n-k)\),那么只需要考虑向内连边的个数,而这个个数也是确定的。容易证明这是充要条件。
CF1779E
给定一个竞赛图,\(n - 1\) 次询问 \(i\) 对集合 \(s\) 出边条数,求出第一个连通分量。
直接询问每个点的度数即可。
1.3. 对出度从小到大排序之后有多少个前缀和是 \(\dbinom{i}{2}\) 的就是 scc 个数。
由上述定理显然。
QOJ5407
【题意】给定 \(n\) 点竞赛图,求对于每一条边,将其反向之后的 \(scc\) 个数。
【分析】
考虑反向是在排序后的数组上 \(+1\) 和 \(-1\)。考虑分讨它们的位置,可以发现是前缀和在某个区间上加或者减了 \(1\)。要注意可能加减后排序的区间会乱掉,但是这个好处理的。
主要是要知道这个结论的用途,不能稍微变个形就不会用了。
2.1. 任意一个 \(n\) 阶强连通竞赛图都包含一个哈密顿回路。
2.2. 任意一个 \(n\) 阶竞赛图都包含一个哈密顿路。
这里注意哈密顿回路和欧拉回路的区别。
哈密顿回路是经过每个点各一次,然后回到起点,只有起点可以到两次。哈密顿回路减去最后回到起点那条路就是哈密顿路,因此有哈密顿回路一定有哈密顿路。这个问题只有指数解法。上次 \(2 \times n\) 的网格图上那道题就是这个模型。
欧拉回路是经过每条边各一次,然后回到起点。这个问题加上“回路”更自然,并且含有充要条件,可以 DFS 求(那个名字很长的算法)。


