根号分治和 unique 模型
1 unique 模型
UVA1608 Non-boring sequences
【题意】
给定长度为 \(n\) 的序列,判断有多少个子序列(连续)满足该序列包含至少一个唯一出现的数。
【分析】
和 djq 上次讲的那个很像,是 unique 模型。也就是说,一个数和它的前驱和后继之间的数,可以组成类似一个单调栈求最大值范围的 \(l,r\) 区间。考虑将其映射到一个二维平面上,变成求矩形面积并。(树形结构也有类似的转化)
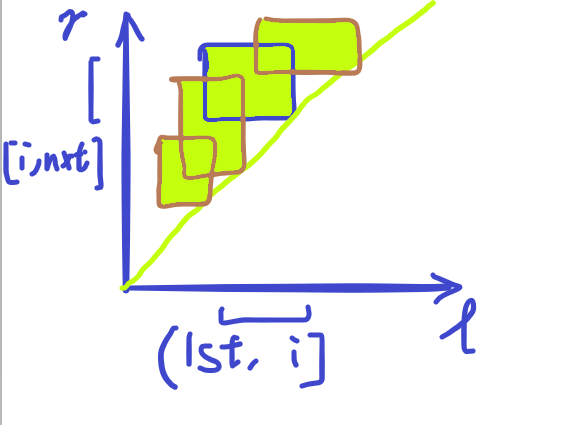
2 根号分治
2.1 根号分治用于时间复杂度证明的技巧
有时候某种“个数限制”会限制“暴力做法”的时间复杂度,证明得到它是对的。
P3396 哈希冲突
【题意】给定 \(v_{1,...,n}\)。
两种操作,第一种修改,\(v_x \rightarrow y\)。第二种查询 \(\sum \limits_{i=1}^n [i \equiv x (\bmod y)] \times v_i\)。
\(n,m \le 10^5\)
考虑对于 \(x \le \sqrt m\),预处理所有这类询问的答案 \(O(m)\),每次修改暴力对于每一个 \(p\) 修改即可,\(O(m\sqrt m)\)。
否则直接暴力查询,一共 \(m\) 次询问,一次只需要查询 \(O(\sqrt m)\) 个数。
2.2 经典 \(k\) 元环计数
无向图三元环计数
\(n,m\) 在 \(O(m\sqrt m)\) 能过级别。
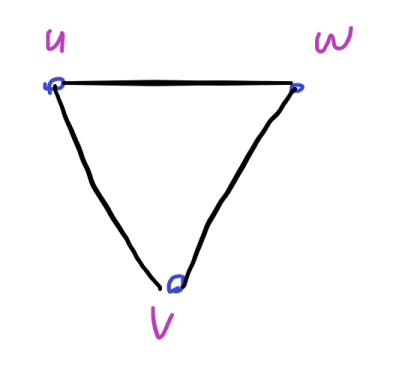
方法是,对边进行定向,按度数排序,度数小的连向度数大的。然后枚举 \(u\),沿着 \(u\) 的出边枚举 \(v\),再沿着 \(v\) 的出边枚举 \(w\),判断 \(u-w\) 是否存在。这种做法不是 \(O(n^3)\) 的,而是 \(O(m\sqrt m)\) 的。为什么呢?
考虑边数在 \(O(m)\) 级别。于是可以证明:每个点定向之后出度 \(O(\sqrt m)\)。这是因为,如果原度数大于 \(\sqrt m\),那么点度大于它的点只有 \(\sqrt m\) 个。
有了这个关键的引理,考虑一条 \((u,v)\) 的贡献为 \(out_v\)。它小于等于 \(m \sqrt m\)。
一个入度 \(\ge \sqrt m\) 的点,它只会被作为 \(v\) 枚举 \(\sqrt m\) 次;
对于一个无序三元组 \((u,v,w)\),如果它们成一个三元环,那么会被枚举到恰好一次。
性质:由于我们每次枚举到一个三元环,所以三元环的个数是 \(O(m \sqrt m)\) 的。
【要点总结】
- 关键的性质是每个点的出度在 \(O(\sqrt m)\) 级别。
- 判断 \(u-w\) 是否有连边,可以先将所有 \(u-v\) 标记上 \(vis = 0\),然后检验;等 \(u\) 将要枚举到下一个点的时候将 \(vis\) 清空。
无向图四元环计数
同样的,找找怎样不重不漏计算。(重复的话一定会损失复杂度)
考虑偏序关系下 \(u < v < w <x\),有六种排列方式,画出来之后发现有这样的形式:
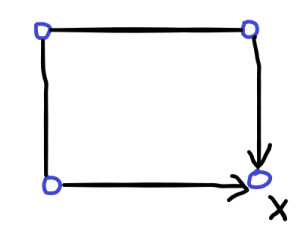
考虑计算的时候以这样的 \(x\) 为关键点即可。
记 \(x\) 对面的点为 \(y\)。考虑每个环,拆成两条 \(y - z \rightarrow x\) 的三元组。那直接从 \(y\) 开始枚举就好了。考虑可以在遍历到一条 \(y - z \rightarrow x\) 的时候先取一次 \(x\) 上的标记,然后再在 \(x\) 上打一个。这样比较好写。
考虑其时间复杂度。一个点的出度依然是 \(O(\sqrt m)\) 级别,而对于每条无向边有 \(out_v\) 的贡献,因此证明与三元环一致,时间复杂度为 \(O(m \sqrt m)\)。
2.3 一个套路:考虑最小值
有时候题目存在乘法,出现根号性质并不好把握,但是一个方向是抓住什么量会 \(\le \sqrt n\),对其下手。
ARC160B Triple Pair
给定 \(N\),求满足 \(xy, yz, zx \le N\) 的有序三元组 \((x,y,z)\) 个数。
\(T \le 100, N \le 10^9\)
注意到乘法形式,会想到整除分块,但是这之后应当想到使用根号分治:假如有个形如 \(\min(a, b) \le \sqrt n\) 这样的形式,那么就想到枚举其中一个 \(\le \sqrt n\) 的元素,然后批量处理另一个元素,这是根号分治的一种重要想法。它比那些使用根号分治进行复杂度分析的“神之一手”更加基础,也更加常见更加套路更加有迹可循,希望熟练掌握。笔者两次遇到均没有朝该方向,于是对比两题加以总结。
本题中显然 \(\min(x, y) \le \sqrt n\)。如果知道 \(x, y\) 那么 \(z\) 取值个数显然为 \(\lfloor\cfrac{n}{\max(x,y)}\rfloor\)。如果枚举 \(x\),那么贡献为 \(\sum \limits_{y \ge x} \lfloor\cfrac{n}{y} \rfloor\),并不是好维护的。
这条路走不通,换一条路,考虑尝试分类讨论。
- 对于 \(x, y\) 都 \(\le \sqrt n\) 的情况,\(z\) 的上界 \(\ge \sqrt n\)。可以枚举 \(\max\)。
- 对于有一个 \(\ge \sqrt n\) 的情况可以让它做 \(z\)!
诶,发现一个依据对称性做的方式,不妨 \(x \le y \le z\),对于三个不同的情况,直接枚举 \(y\),然后考虑其所有置换即可;对于两个相同的情况和一个相同的情况也可以容易容斥掉。
这题其实不算根号分治,但是它提示了我们根号做法不只有整除分块,还可以通过分类讨论发现一些东西。
CF1830B The BOSS Can Count Pairs
给定数列 \(a, b\) 长度均为 \(n\)。求有序数对 \((i, j)\) 满足 \(a_i a_j = b_i + b_j\) 的数量。
\(\sum n \le 2 \times 10^5,1 \le a_i, b_i \le n\)
首先注意到对于一个 \(i\),所求的是一条线 \(a_ix - b_i = y\) 上的点数。但是这并没有什么快速维护的方式。
注意到题目里的 \(a_ia_j\) 形式以及 \(a_i \le n\),发现对于一个 \(a_i\),另一个 \(a_j\) 的取值范围在 \(\lfloor\cfrac{2n}{a_i}\rfloor\) 以下。这是否意味着我们可以调和级数做?
想到一个做法:枚举 \(x\),先将所有 \(a_j \le \lfloor \cfrac{2n}{x} \rfloor\) 的 \((a_j, b_j)\) 存起来,然后用 \(a_i = x\) 的所有 \(b_i\) 去匹配。但是你注意一些的话可以发现这个做法虽然过了 pp,但是时间很大,不像是 \(O(n \log n)\) 的(笔者赛时没发现,然后 FST 了)。你会发现如果将 \(a_i=x\) 的所有数比喻成“\(x\) 箱子里的东西”,那么如果 \(1\) 箱子里有 \(O(n)\) 个数,将会退化到 \(O(n^2)\)。
再进行思考,因为 \(i\) 和 \(j\) 是一个相互配对的关系,貌似并没有什么方法将配对过程简化。有一种做法是 \(\sum \limits_{(i,j)} \min(|box_i|, |box_j|)\) 的,但是当 \(\forall i, |box_i| = 1\) 的时候依然是 \(O(n^2)\) 的。
这时候就需要对 \(a_ia_j\) 这个形式进行再次审视,发现关键性质了:\(\min(a_i, a_j) \le \sqrt{2n}\)!这样的话,我们可以枚举 \(\min(a_i, a_j)\),然后配对另一个,这样时间复杂度就变成了 \(O(n \sqrt n)\)。


